 コッホ曲線の生成
コッホ曲線の生成
 コッホ曲線の生成
コッホ曲線の生成
コッホ曲線のようなフラクタル図形の描画は,関数の再帰呼び出しを使うことに よって容易に実現できる. 以下はポストスクリプト言語によってコッホ曲線を描画する例である. 関数kochには再帰の深さlevelと線分の長さlenがスタック経由で渡される. 関数kochの中では, levelを1減らし,線分の長さを3で割って,線分の方向を 0→+60→-120→+60と変えながら,再び四回kochを呼び出している. もしlevelが0に達すると,長さlenの直線を描画する.
%!
/ed {exch def} def
/koch { % level len
2 dict begin /len ed /level ed
level 1 ge {
level 1 sub len 3 div
2 copy koch
2 copy 60 rotate koch
2 copy -120 rotate koch
60 rotate koch
}{
len 0 rlineto
} ifelse
end
} def
/kochcurve { % level len x0 y0
gsave translate 0.1 setlinewidth
newpath 0 0 moveto koch stroke
grestore
} def
1 setlinecap 1 setlinejoin
5 400 100 100 kochcurve
showpage
本文に戻る
 ボックスカウント法によるフラクタル次元の測定
ボックスカウント法によるフラクタル次元の測定
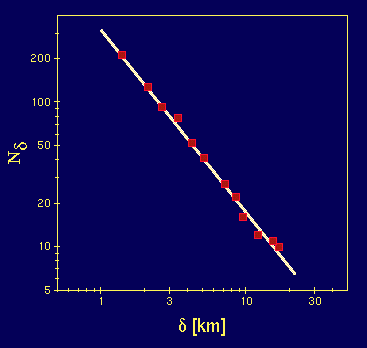 図は宮城県から岩手県にかけての三陸地方の海岸線である.
この海岸線を覆うために必要なボックスの個数を
ボックスの大きさを変えながら実際に数え上げた例を示す.
20km程度から1km程度の範囲で,Nδ〜δーDB
がよく成り立っていることが分かる.
この両対数プロットの勾配を最小二乗法で見積もると,およそ-1.27であった.
すなわちこの場合の海岸線のフラクタル次元はおよそDB≒1.27と
推定される.
図は宮城県から岩手県にかけての三陸地方の海岸線である.
この海岸線を覆うために必要なボックスの個数を
ボックスの大きさを変えながら実際に数え上げた例を示す.
20km程度から1km程度の範囲で,Nδ〜δーDB
がよく成り立っていることが分かる.
この両対数プロットの勾配を最小二乗法で見積もると,およそ-1.27であった.
すなわちこの場合の海岸線のフラクタル次元はおよそDB≒1.27と
推定される.
 縮小写像による自己アフィンフラクタルの生成
縮小写像による自己アフィンフラクタルの生成
二次元平面上でのアフィン変換を表わす2行2列の行列をAで,
平行移動をベクトルTで表現することにしよう.
縮小写像Siを
Si:x→Aix+Ti
と書く.
行列Aの成分を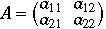 ,
,
ベクトルTの成分を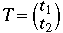
とすると,
この例はそれぞれの成分が以下のような
4つの写像を組み合わせて描画した.
| i | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| a11 | 0.85 | 0.2 | -0.15 | 0 |
| a12 | 0.04 | -0.26 | 0.28 | 0 |
| a21 | -0.04 | 0.23 | 0.26 | 0 |
| a22 | 0.85 | 0.22 | 0.24 | 0.16 |
| t1 | 0 | 0 | 0 | 0 |
| t2 | 1.6 | 1.6 | 0.44 | 0 |
 Weierstrass関数
Weierstrass関数
 自己アフィン曲線の生成
自己アフィン曲線の生成
この生成規則にしたがってさらに反復を繰り返すと下図のような グラフが得られる.グラフと水平線(赤線)との交差する点集合の フラクタル次元は1/2である.
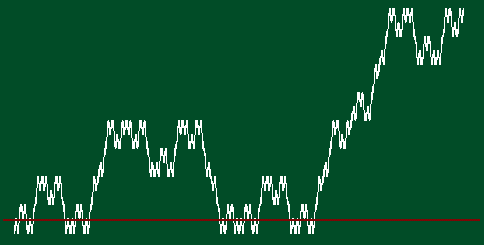
 一般化次元とfーαスペクトルの性質
一般化次元とfーαスペクトルの性質
 異なる空隙性を持つカントール集合
異なる空隙性を持つカントール集合
 パーコレーションクラスターの一部
パーコレーションクラスターの一部
二次元サイトパーコレーションを500×500の正方格子上で行い, その最大クラスターの一部をプロットした. シミュレーションはp=pcで行った. 二次元正方格子上でのサイトパーコレーションの臨界確率は pc=0.592745…であることが知られている. これに対して, 正方格子のボンドモデルではpc=0.5, 三角格子のサイトモデルでもpc=0.5,そして 三角格子のボンドモデルではpc=0.34729…であることが 知られている. クラスターのフラクタル次元はいずれの場合も91/48=1.895…である.
 ブラウン粒子の非可逆的な凝集の繰り返しによって成長する
diffusion-limited aggregation (DLA) は,パーコレーションモデルと
同様に,フラクタルな凝集体(クラスター)が現われる例として
よく知られている.
二次元でのDLAクラスターのフラクタル次元はD=1.71程度であって,
パーコレーションクラスターのそれに較べて低い(左図).
このことは,クラスターの密度が低く,全体に「すかすか」に見える
ことからも直感される.
DLAクラスターがパーコレーションクラスターと異なる点はフラクタル次元
のみではない.例えば,DLAクラスターは中心から放射状に広がっており,
外側に向かって「開いた」構造である.
基本的なクラスターの構造は単連結で,ループはない.
また,三次元のパーコレーションとDLAはいずれもクラスターのフラクタル
次元が2.5であることが知られているが,二次元と同様,その構造
は非常に異なる.
ブラウン粒子の非可逆的な凝集の繰り返しによって成長する
diffusion-limited aggregation (DLA) は,パーコレーションモデルと
同様に,フラクタルな凝集体(クラスター)が現われる例として
よく知られている.
二次元でのDLAクラスターのフラクタル次元はD=1.71程度であって,
パーコレーションクラスターのそれに較べて低い(左図).
このことは,クラスターの密度が低く,全体に「すかすか」に見える
ことからも直感される.
DLAクラスターがパーコレーションクラスターと異なる点はフラクタル次元
のみではない.例えば,DLAクラスターは中心から放射状に広がっており,
外側に向かって「開いた」構造である.
基本的なクラスターの構造は単連結で,ループはない.
また,三次元のパーコレーションとDLAはいずれもクラスターのフラクタル
次元が2.5であることが知られているが,二次元と同様,その構造
は非常に異なる.