 自己相似と自己アフィン
自己相似と自己アフィン
 自己相似と自己アフィン
自己相似と自己アフィン
前節では暗黙のうちに対象を等方的なフラクタルに限定していた. フラクタル図形は等方的なスケール変換によって部分が全体と一致する性質 を有する. これに対してアフィン変換によって部分が全体に一致するような図形を 自己アフィンと呼び,あらゆるスケールで自己アフィンである図形を 自己アフィンフラクタル(self-affine fractal)と呼ぶ.
複雑な形状の山の稜線をはるか遠方から眺めた場合に,山の起伏は比較的 なだらかに見えるが,近づくにつれて急な斜面や崖が目立ち始める. すなわち,横方向と上下方向でスケールの拡大率を変えることによって, 初めて相似性が見いだされる. 事実,いくつかの山地では,稜線が自己アフィンフラクタルでよく表現される ことが報告されている. 自己アフィンは,複雑な時系列や表面の形状を特徴付ける際に使われる一方で, 自己相似なフラクタルとしばしば混同されることがあるので注意が必要である.
複数のアフィン変換を組み合わせた縮小写像を用いると,自己アフィン フラクタルを簡単な規則で生成することができる. Rnの部分集合DからDへの写像Sを考えよう. Sによって集合上の二点間の距離が常に縮小される, すなわち |S(x)ー S(y)|≦|xーy| を満たす0<c<1が存在するとき,Sを縮小写像という. m種類の縮小写像S1,…,Smの組を与えると,
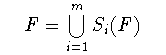 (2-1)
(2-1)
Si(F)が互いに重なり合わず,Siのそれぞれが等方的 な縮小写像であるとき,すなわち
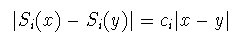
 そのとき
そのとき
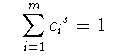
 自己アフィンなグラフと曲面
自己アフィンなグラフと曲面
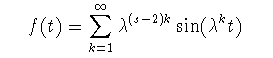 (2-2)
(2-2)
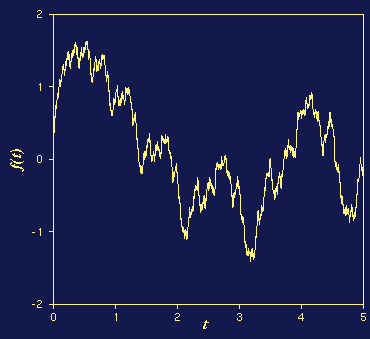
f(t)が自己アフィンである場合に,それを特徴付ける指標として荒さ指数 (roughness exponent)またはハースト指数(Hurst exponent)が歴史的に用いら れている. ある「時間」間隔δの間のf(t)の平均二乗偏差を
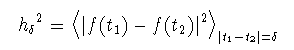 (2-3)
(2-3)
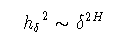 (2-4)
(2-4)
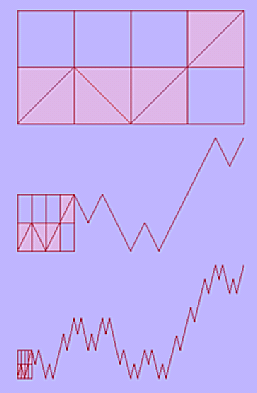 このとき,黒く塗られた部分が互いに隣接しグラフの連結性が保持される
ように,部分的に上下を反転させながら手続きを繰り返すことにより
自己アフィンなグラフを生成できる.
このグラフと水平直線との交差は自己相似なフラクタル
になり,ボックスの大きさと水平方向の黒いボックスの数の関係から,
フラクタル次元はDh=1/2であることがわかる.
一方,垂直方向の線分との交差は一点であって,そのフラクタル次元は
Dv=0であることは自明である.
グラフ(自己アフィン曲線)において,横方向を変数tに,縦方向をtに対する
変量f(t)と見做すと,このようにあいまいさなく軸を設定でき,
縦方向の線分との交差のフラクタル次元は常にDv
であって,横方向のフラクタル次元は0<Dh<1である.
また,この生成規則によれば,横方向と横方向のスケール変換率から,
この例ではH=1/2であることも容易に示せる.
一般には,ハースト指数と,f(t)の横断面のフラクタル次元Dh
とは
このとき,黒く塗られた部分が互いに隣接しグラフの連結性が保持される
ように,部分的に上下を反転させながら手続きを繰り返すことにより
自己アフィンなグラフを生成できる.
このグラフと水平直線との交差は自己相似なフラクタル
になり,ボックスの大きさと水平方向の黒いボックスの数の関係から,
フラクタル次元はDh=1/2であることがわかる.
一方,垂直方向の線分との交差は一点であって,そのフラクタル次元は
Dv=0であることは自明である.
グラフ(自己アフィン曲線)において,横方向を変数tに,縦方向をtに対する
変量f(t)と見做すと,このようにあいまいさなく軸を設定でき,
縦方向の線分との交差のフラクタル次元は常にDv
であって,横方向のフラクタル次元は0<Dh<1である.
また,この生成規則によれば,横方向と横方向のスケール変換率から,
この例ではH=1/2であることも容易に示せる.
一般には,ハースト指数と,f(t)の横断面のフラクタル次元Dh
とは
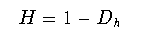 (2-5)
(2-5)
ハースト指数Hを持つ自己アフィン曲線について,フラクタル曲線の 場合と同様にしてボックス次元を計算するとどうなるであろうか. 時間間隔δの間のfの平均的な変動幅はδHであるから, δの時間間隔内で曲線が占める領域の大きさはδ1+H程度 となる. よってそれを覆うに必要なボックスの数は
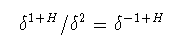
一次元ランダムウォークは自己アフィンなグラフのよい例である. 一次元ランダムウォークの時刻tでの変位をf(t)とすると, そのグラフを特徴付ける指数はそれぞれH=Dh=1/2である. このことはランダムウォークにおいて平均二乗移動距離が経過時間に比例 すること,および再帰点の集合(f(t)=0であるようなtの点集合)のフラクタル 次元が1/2であることに対応している. 言い換えると,ブラウン運動過程はH=1/2を与え,これは各時刻の増分が 互いに独立(無相関)であることに関係する. これに対して,増分に長時間相関があり,f(t)が自己アフィンな曲線となる 過程を非整数ブラウン運動(fractional Brownian motion: fBm)と呼ぶ. fBmではハースト指数は1/2以外の値を取る. 時間相関のないガウス過程に従うランダムな増分をdB(t)で表記すると, 確率積分
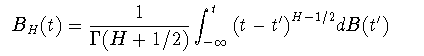 (2-6)
(2-6)
二変数関数f(x,y)で表わされる自己アフィン曲面でも, 二点間の距離に対する高さの二乗変位の関係からハースト指数Hを同様に 定義できる. このような曲面の等高線はフラクタルであって,そのフラクタル次元を Dhとすると
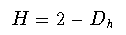 (2-7)
(2-7)
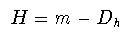 (2-8)
(2-8)
 ハースト指数の計測
ハースト指数の計測
非定常で複雑な時系列を特徴付けたり,複雑な物体表面の形状を表わす際には しばしばハースト指数が用いられる. 以下に,ハースト指数の実際的な測定方法を三種類挙げた.
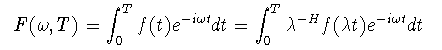
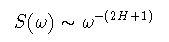 (2-9)
(2-9)
この方法と関連して,ブラウン運動の回帰確率からHを推定することも できる. t0以降にf(t0+δ)=f(t0)が初めて 実現される確率をp(δ)とすると,
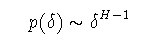 (2-10)
(2-10)