 フラクタル幾何
フラクタル幾何
 フラクタル幾何
フラクタル幾何
三陸地方のリアス式海岸やノルウェーのフィヨルドなどの海岸線を
地図の縮尺を変えながら見ても,そこには類似の構造が再帰的に現れる.
すなわち,地図上のスケールはこのような海岸線の特徴を表現するためには
役に立たない.
一方で,フラクタル図形の例として知られるコッホ曲線(von Koch curve)
は,どこかしらこうした海岸線の特徴をよくとらえているように思われる.
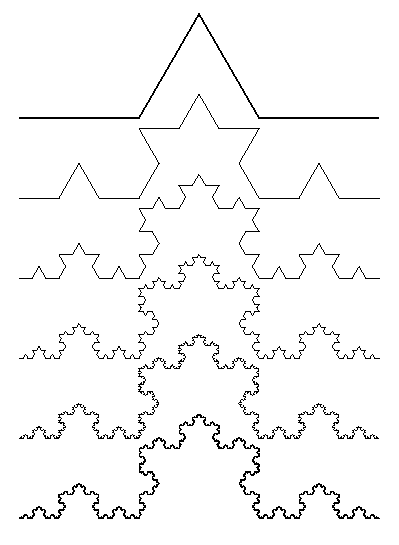 図のように,
コッホ曲線は線分のそれぞれの部分を1/3倍の長さの4つの線分で置き換えて
いく操作を繰り返すことによって得られる図形で,
いたるところ微分不可能で,しかもトポロジカルには曲線のままでありながら,
その全長が発散するような,一見常識的ではない性質をもつ.
図のように,
コッホ曲線は線分のそれぞれの部分を1/3倍の長さの4つの線分で置き換えて
いく操作を繰り返すことによって得られる図形で,
いたるところ微分不可能で,しかもトポロジカルには曲線のままでありながら,
その全長が発散するような,一見常識的ではない性質をもつ.
フラクタル(fractal)はマンデルブロ(B.B.Mandelbrot)の造語で,このように 微分不可能で,解析的な取り扱いには馴染まない図形を語る言葉として, 1970年代以降広く用いられるようになった. そして,海岸線をはじめとする様々な自然の造形と幾何学との 接点が得られるようになったのである. しかしながら,マンデルブロの著作がそうであるように,フラクタルという 用語はかなり広い意味で使われており,幾何学的な概念を越えて, 物理数学の広範な分野と関わりを持つに至っている.
本節以下ではまず,フラクタルの定量的な表現であるフラクタル次元 (fractal dimension)を与えるために,ハウスドルフ測度とハウスドルフ次元 の定義と性質の説明から始め,次いで,その他のフラクタル次元の定義との関連に ついて触れることにしよう.
 ハウスドルフ次元(Housdroff-Besicovitch dimension)
ハウスドルフ次元(Housdroff-Besicovitch dimension)
n次元ユークリッド空間の部分集合をUとする. そのときUの径を
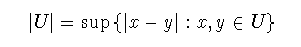 (1-1)
(1-1)
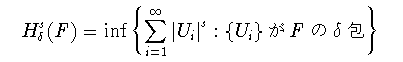 (1-2)
(1-2)
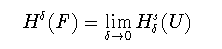 (1-3)
(1-3)
例えばFとして線分を考えると,s<1のときHsは無限大に, s>1ではHsは0になることが容易に示せる. 集合Fのハウスドルフ次元DH(F)とは ハウスドルフ測度が0と無限大のちょうど境界になるような sの値であって,与えられた集合について唯一定まる:
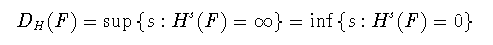 (1-4)
(1-4)
点のハウスドルフ次元は0,曲線は1,曲面は2,立体では3となり, これらは我々の直感ともよく一致する. つまり通常の線や面のハウスドルフ次元は,そのトポロジカルな次元に等しい. これに対して,
さらに,ハウスドルフ次元には以下のような性質があることが知られている.
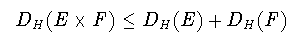 (1-5)
(1-5)
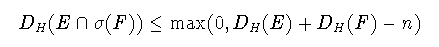 (1-6)
(1-6)
その定義から点集合Fのスケールをλ倍に変換した際に,それに 対応するハウスドルフ測度はλs倍にスケールされる. すなわち,λF={λx:x∈F}に対して
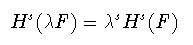 (1-7)
(1-7)
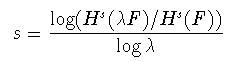 (1-8)
(1-8)
では,よく知られたフラクタル図形であるコッホ曲線のハウスドルフ次元を はどのような値を取るのであろうか. コッホ曲線の生成規則によれば,第k番目の反復では3-kの長さの 線分が4k本生成される. このことから,直径δ=3-kの円でコッホ曲線を覆うために必要な 円の数が4kであることは容易に推察できるから
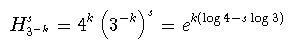 (1-9)
(1-9)
 相似次元(similarity dimension)
相似次元(similarity dimension)
集合Fそれ自身のサイズを縮小して得られる 集合の(互いに重なりのない)和集合が,再びFに一致するような集合を 自己相似(self-similar)であると言う. F全体を構成するために必要な部分集合の数をN,縮尺率をr(<1) とすると,相似次元DSは
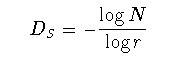 (1-10)
(1-10)
コッホ曲線は,縮尺率1/3であるような互いに重ならない4つの部品 から全体を構成できるから,相似次元は DS= - log 4/log (1/3) = log 4/log 3 である. この例のように,簡単な生成規則が与えられたフラクタル図形については 相似次元の導出は容易である.
 ボックス次元(box dimension)
ボックス次元(box dimension)
集合Fを大きさδの箱(ボックス)で覆うために必要 なボックスの個数をNδ(F)とすると,ボックス次元は
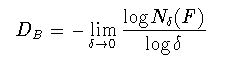 (1-11)
(1-11)
ボックス次元とハウスドルフ次元との間には
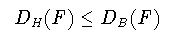 (1-12)
(1-12)
 フラクタル次元の測定方法
フラクタル次元の測定方法
幾何学的なフラクタル図形の場合は,相似次元やボックス次元を 直接計算することによってフラクタル次元を求めることができるが, 実験やコンピュータ・シミュレーションで得られたデータのフラクタル次元を 求める際には,いくつかのより実際的な手法が使われている.
ボックス次元はボックスの選び方に敏感ではないため,実際的な次元の 測定に際しても適用度が大きい. 海岸線のように複雑な曲線のフラクタル次元を測る際によく使われる デバイダ法は,歩幅δを様々に変えながら,曲線上の端から 端までを歩くために必要な歩数Nδを調べ,これらの両対数 プロットの勾配
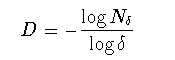 (1-13)
(1-13)
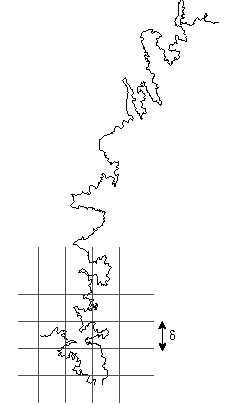 実験の解析等で多用されるのは,碁盤の目のように,空間を等間隔δの
格子状の領域に分割し,図形の一部が含まれるようなボックスの
数Nδから上と同様に次元を推定する方法である
(図参照).
実験の解析等で多用されるのは,碁盤の目のように,空間を等間隔δの
格子状の領域に分割し,図形の一部が含まれるようなボックスの
数Nδから上と同様に次元を推定する方法である
(図参照).
一般にボックスカウント法では,ボックスの選び方(図形と ボックスの位置関係)によって得られる次元の値にばらつきが生じることが多い. そのため,データによっては,ボックスの位置を幾通りも変えるなどして Nδの見積もりの誤差を減らすための工夫が必要である. 例えば,コッホ曲線の画像データからフラクタル次元を数値的に求める手順を 想定してみよう. コッホ曲線は長さスケール1/3毎に同じ構造が再帰的に現れるため,ボックスの 取り方によっては,δの両対数プロットはlog 3の周期で振動 しているように見えるであろう. これは,空隙性(4節)の大きな集合で特に顕著である. このような場合は,δの変化の範囲を十分広く取り, log Nδ−log δプロットの全体的な勾配から次元を推定 しなければならない.
n次元空間内の密度分布ρ(x)に対して相関関数C(r)を
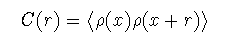 (1-14)
(1-14)
分布がスケール不変(フラクタル)であるとは,スケール変換率をλ とすると
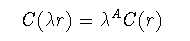 (1-15)
(1-15)
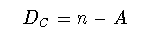 (1-16)
(1-16)
サイズ$\delta$の球内での分布の総量は,空間次元が$n$であることに注意すると,
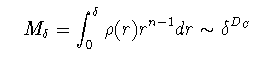
散乱実験などでは,波動の性質から密度相関のフーリエ成分がデータとして 得られる. フラクタルな分布では上記のように相関関数が距離のべき乗関数になるため, 相関関数のフーリエ変換であるパワースペクトルもまた波数に対して べき乗関数となる.すなわち,等方性を仮定すれば,
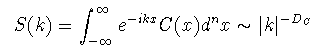 (1-17)
(1-17)
測定対象が点集合である場合は,積分された二点相関を直接計算する方法が よく用いられる. Rn中の点集合を{Xi}(i=1…N)とし,二点間の距離を |XiーXj|で表記すると, 積分された相関関数は
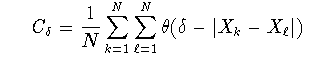 (1-18)
(1-18)
長さLの線分から開始して,コッホ曲線を生成した場合に,得られた曲線の 唯一の特徴的な長さはLであって,Lよりも小さなスケールでは自己相似な 構造が繰り返される. 様々な長さLiから生成したコッホ曲線が多数個存在する場合に, それぞれの コッホ曲線の「断片」は自己相似であると同時に,互いにも相似な図形と言える. ある固定されたサイズδ(《Li)のボックスでLiの 曲線を覆うに必要なボックスの数を Nδ(Li)とすると,
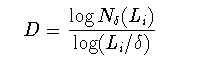 (1-19)
(1-19)
特徴的なサイズLの決め方としては,図形の最大の差しわたしの長さや, 回転半径(gyration radius)を採用する場合が多い. 図形を構成する点の座標を{xi}(i=1 … N)とすると, 回転半径Lgは
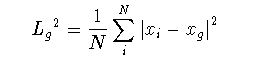 (1-20)
(1-20)
回転半径と図形の質量(体積)の関係からフラクタル次元を計算する方法は, 高分子の構造や自己相似に成長するパターンの研究ではしばしば用いられる. 例えば,理想高分子鎖のモデルであるランダムウォークは,歩数(モノマーの数) Nと平均的な鎖の長さξ(N)との間にξ〜N1/2なる関係が 成立するが,このことは理想高分子鎖のフラクタル次元が2であることを意味する.
境界がフラクタルであるような領域については,特徴的な長さを領域の面積 ないし体積で評価することもできる. 境界が複雑に入り組む「島」が多数点在する場合には,島の面積をAi とすると, それぞれの島の特徴的な長さはLi〜Ai1/2 である. このとき,島の周囲をある一定サイズδのボックスで覆うために必要 なボックスの個数Nδは
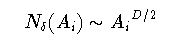 (1-21)
(1-21)