 べき乗分布
べき乗分布
 べき乗分布
べき乗分布
フラクタルの物理的な内容は「特徴的なスケールが存在しないこと」である. コッホ曲線などの幾何学的なフラクタル図形は,どのような物差しで 見ても部分と全体が互いに相似であって,それを特徴付ける長さは 存在しない.このことは,自己アフィンフラクタル図形であっても, あるいはマルチフラクタルな分布であっても同様である.
この考えをさらに進めて,特徴的な量や数が存在しないような系に 対して,フラクタルという呼称を用いる場合が少なくない. 一般に,ある物理量Xがξに対してX〜ξーβのように 振る舞う場合にはXに関するξの特徴的な大きさが見いだせない. あるいは,ξのスケール変換に対してXの性質を不変に保つような関数関係 がべき乗関数であるとも言える. この意味で,べき乗則とフラクタルとは同義的に用いられることもある.
自然現象や社会現象を解析すると,しばしばべき乗分布が登場する. 都市毎の人口分布や英単語毎の出現回数など多くの事例について, 順位(ランク)をk,それに対応するサイズ(人口や出現回数)をxとすると, x〜kーβのような逆べきの関係がよく成り立つことが知られており, ジップ(Zipf)の法則と呼ばれることがある. サイズがxとx+dxの間にあるような場合の数を分布関数ρ(x)を使って ρ(x)dxと書くと,ジップ則はサイズ分布関数がべき乗分布
 空隙とファットフラクタル
空隙とファットフラクタル
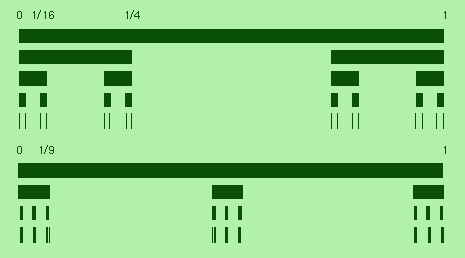 これらの結果得られる集合の測度は0で,フラクタル次元はいずれの場合でも
D=1/2となる.
このように,同一のフラクタル次元であっても点の分布の様子が大きく異
なって見える場合があるが,これを特徴付けるよい指標はないであろうか.
こうした分布の空間的な揺らぎの性質は空隙性(lacunarity)と呼ばれている.
空隙性を特徴付けるためのいくつかの方法が提案されているが,
ここでは分布のモーメント比を利用した方法を紹介しよう.
フラクタルな集合Fを含むようなRnの領域Rを考え,
その中でのサイズδのボックスの中の測度μの分布確率を
P(μ,δ)とする.
以下でそのn次モーメントを定義する.
これらの結果得られる集合の測度は0で,フラクタル次元はいずれの場合でも
D=1/2となる.
このように,同一のフラクタル次元であっても点の分布の様子が大きく異
なって見える場合があるが,これを特徴付けるよい指標はないであろうか.
こうした分布の空間的な揺らぎの性質は空隙性(lacunarity)と呼ばれている.
空隙性を特徴付けるためのいくつかの方法が提案されているが,
ここでは分布のモーメント比を利用した方法を紹介しよう.
フラクタルな集合Fを含むようなRnの領域Rを考え,
その中でのサイズδのボックスの中の測度μの分布確率を
P(μ,δ)とする.
以下でそのn次モーメントを定義する.
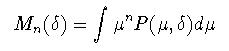 (4-1)
(4-1)
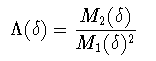 (4-2)
(4-2)
カオスアトラクタの構造などを詳しく解析すると, 測度が0でないような集合で,かつその境界(外周)部分の構造が自己相似性 であるような集合が現れる場合がある. 測度が0でないことから,これはファット・フラクタル(fat fractal)と呼ばれている. ファット・フラクタルに通常のフラクタル次元の定義を適用すると, その次元は空間次元に一致するため,ファットフラクタルを特徴付けるため に以下のようなフラクタル次元が考案されている.
フラクタルな集合S0⊂Rnの周にサイズδのn次元 ボックスを加えて集合Sδを構成する. サイズδのボックスで,この集合を覆うために必要なボックスの 数をNδとすると,ボックスで覆われた体積は
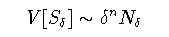
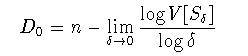
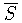 について同様な次元
について同様な次元
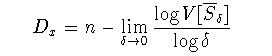 (4-3)
(4-3)
 臨界現象とフラクタル
臨界現象とフラクタル
物質が温度などのパラメータによってその秩序(対称性)を突然 変える現象,すなわち相転移は,今世紀に飛躍的に理解が進んだ 物理数学の分野である. そして,フラクタルという用語がよく知られるようになる以前から スケーリングや繰り込みなど,フラクタルと関係の深い概念が 知られていた. 最後に,比較的性質のよく調べられている臨界現象のモデルとして パーコレーション(percolation)を取り上げ,そこに現れる様々な フラクタル性を紹介する.
n次元の格子(例えば立方格子)を与え,そのサイト(あるいはボンド)部分をある 確率pで占有する手続きを考えよう. もしp≒1ならばサイトは全て連結され,格子全体のネットワークが形成 されるであろう.反対にp≒0の場合には,占有されたサイトは殆どなく, 占有されたサイトがあったとしてもその周囲は空のままであろう. このように,空間の点あるいはボンドが確率的に占有される過程を パーコレーション(浸透)と呼ぶ. これは,ランダムな媒質中を液体が浸透する過程や,森林火災が伝搬する 過程を理想化したモデルと考えることができる.
パーコレーション問題では,p>pcで初めて無限大の大きさの 連結されたボンド(またはサイト)のクラスターが出現するような臨界確率 cが存在し, その値は空間次元,ボンドを占有するかサイトを占有するか, 格子の種類などに依存して決まる. あるボンド(あるいはサイト)がその無限大クラスターに属する確率は p>pcにおいて
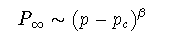 (4-4)
(4-4)
相転移点pc近傍では,あらゆる物理量が異常性を示す.ボンド(サイト) が互いに連結している領域(クラスター)のサイズξは, ξ〜|pーpc|ーν のように(ξは相関距離と呼ばれる),クラスターに含まれる平均的な ボンド(サイト)の数SはS〜|pーpc|ーγのように, いずれも臨界点の近傍でべき乗関数で発散する. pcは格子の形状などのモデルの詳細には依存するものの, β,ν,γ などの指数はモデルの詳細に依らないという意味で普遍性(universality)を持つ. 相転移点の近傍での相関距離が発散は,系の特徴的な長さがpcでは 存在しなくなることを意味する. 事実,pcで生じる無限大サイズのクラスターはフラクタルであって, そのフラクタル次元はD=nーβ/νで与えられることが知られている (図).
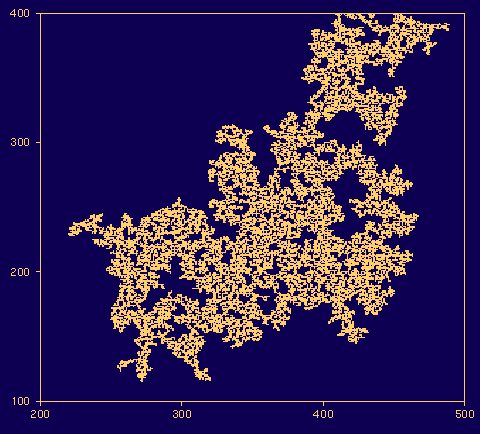
フラクタル次元はクラスターの形状を特徴付けるために有力な指標には違い
ないものの,クラスターのさらに詳細な構造や物性を記述するために,いくつか
の異なる「次元」が考案されている.
ユークリッド距離r離れたパーコレーションクラスター上の二点間の,
クラスターに添ったパスの最短の長さを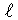 とすると,
とすると,
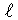 〜rDmin
なる関係があり,クラスター内部の構造を反映して,Dminは
1以外の値を取る.
これは,クラスター内の連結性に関係した次元であると考えることができる.
〜rDmin
なる関係があり,クラスター内部の構造を反映して,Dminは
1以外の値を取る.
これは,クラスター内の連結性に関係した次元であると考えることができる.
また,パーコレーションクラスターは,それ自身がフラクタルであるような いくつかの部分集合に分けられることも知られている. 仮想的にクラスターの両端に電極を繋いて電流を流した場合に, 電流が流れる経路にあたる部分をバックボーン(backbone)と言い,電流に 寄与しない部分をダングリング端(dangling end)と言う. バックボーンはクラスターよりも小さなフラクタル次元を持つクラスターの一部で, さらにその中で全体の連結性のかなめになっている(そのボンドを切断す ると電流の迂回路が他に存在しないような)ボンドをレッドボンド(red bond)と呼ぶ. レッドボンドはバックボーンよりもさらに小さなフラクタル次元を持つ. このように,現象によっては,フラクタルな集合の上にさらに意味のある フラクタル部分集合が定義出来る場合がある.
複雑な物質やネットワークを経由するような輸送現象では,しばしば 異常な拡散や応答が見られる. フラクタルなパーコレーションクラスターの上に制限された ランダムウォークを考えよう. 時間tが経過した後での,ウォーカーの平均二乗移動距離は
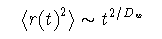 (4-5)
(4-5)
フラクタルな構造中で励起される振動モードをフラクトン(fracton)と 呼ぶことがある. n次元結晶格子中の振動数ωのフォノンの状態密度n(ω) がn(ω)〜ωn-1に従うのに対して,パーコレーション クラスター等のフラクタル構造では
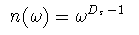 (4-6)
(4-6)