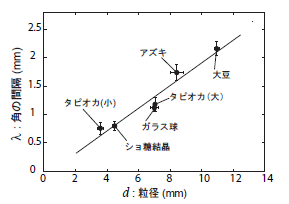
直線はλ = 0.2 d
次に、我々が得た結果のいくつかを紹介しよう。
サイズの異なるいくつかの種粒子(いずれもほぼ球形)を選び、初期の角がはじめて確認された時点でいくつかの結晶を取り出して、粒子サイズと、生えた角の間隔をプロットしたのが図3である。図から明らかなように、初期の角の間隔は、粒子の径にほぼ比例しており、角の間隔 λと直径d の関係はλ = 0.2 d でよく近似できる。球面上に角が等間隔に生えていると仮定すると、この比例係数から、ごく初期の角の本数は、粒子径によらず90本程度であったと推定できる。
 |
図3: 成長初期に発生した角の間隔と、種粒子の直径との関係。 直線はλ = 0.2 d |
図4は、成長過程の角の本数分布を示しており、時間経過とともに、角の本数が次第に減じられ、分布の幅が狭まっている様子が分かる。そして、成長の終盤では、角の本数は20本〜24本程度に落ち着いている。最終的に選ばれる角の本数は、同じ条件下でも実験毎に異なる場合があって、図4の挿入図は角の分布のピークが20本の例である。
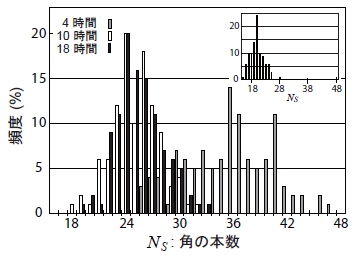 |
図4:角の本数の分布。成長開始から4, 10, 18時間経過後の 約100個の試料について計測。挿入図は、同じ条件で行った 異なる試行についての18時間後の分布で、分布のピーク位置 は必ずしも一致しない。 |
このように、球形の種から出発した場合、初期に90本程度の多数の角が発生し、それが次第に減じられ、比較的狭い分布幅を持った定常状態に至る、という見方が妥当なようである。成長過程での角の選択過程をさらに詳しく見るために、途中で粒子をサンプリングしながら、角の間隔の変化を調べてみた結果が図5である。種粒子の径は3mmで、何通りかの流量について繰り返し実験を行った結果をまとめてある。
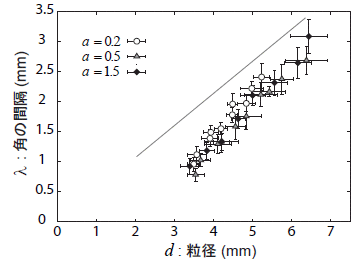 |
図5:成長過程での角と角の間隔の変化。 ショ糖液の供給量が異なる実験をプロット。 種粒子として3mmの球を用いた。 直線は、角の位置が正12面体の20個の頂点の 位置にあったとした場合の、粒子径と間隔の関係。 |
ショ糖液の流量を10倍以上変化させても、ほぼ同様の曲線上に測定点が分布していることから、溶液の供給量は角のサイズ(間隔)を決める主要因ではないだろうと推察できる。もちろん、供給量に応じて金平糖の成長速度は決まるので、流量を決める係数$a$の大きさに応じて、より早く大きな金平糖が得られる。
ある程度成長が進むと、角の間隔と粒子の大きさに比例関係が見られることから、この段階での金平糖は相似形を保ったまま成長していると考えられる。角の間隔のみでなく、角の相対的な高さについても、こうした比例関係は確認されており、角の先端で計った粒子の径d1と、窪みの位置で計った粒子の径 2の比率d2/d1は、成長後期ではほぼ0.6で一定であった。つまり、角の尖り具合についてもある種の相似性が成り立っている。
図5には、角の位置が正12面体の20個の頂点に位置すると仮定した場合の角の間隔と粒子のサイズの関係を実線で示した。測定結果がほぼこの直線に漸近するように見えることから、いずれの場合でも、およそ20本程度の角が選択されていることが伺える。
福島らは市販の金平糖について角の本数を調べ、27〜28本程度が最終的に選ばれるらしいと報告しているが[2]、我々の実験ではさらに少ない本数が示唆された。こうした不一致は、おそらく、成長のどの段階の試料を計測に用いたかの違によって生じたのではないかと、我々は考えている。福島らの測定では角の発達具合の指標 d2/d1 が0.8程度とされており、このことからも、角が十分に発達していない試料が用いられた可能性が高い。
© Yoshinori Hayakawa (2007)