実験から得られた知見からは、多数の粒子を攪拌しながら糖蜜を徐々に加えるという、金平糖に特有の製造プロセスは、とても巧妙な仕掛けに見えてくる。そして、綺麗に角を生やすには
が大切なようである。
ショ糖液の供給量が多すぎると、表面張力で粒子同士が癒着した状態で結晶化してしまうものの、輸液量を加減することによって、粉体の流動によって全ての粒子の表面は「自動的に」くまなく糖蜜で濡らされる。
成長の過程で粒径の異なる結晶が一旦生じてしまうと、有名な「ブラジルナッツ効果」のように、サイズの異なるもの同士で分離してしまう可能性がある。この実験に近い系として、円筒形の回転ドラムの中で粉体が回転軸方向に偏析する現象がよく知られている。粒径の異なる粉体をシリンダー状のドラムに入れて、軸を水平した状態でゆっくりと回転させると、回転軸(水平)方向に大小の粒子が分離し、「バンド」構造を呈する場合がある[9]。我々の実験でも、ドラムの回転速度の選択によっては、これに近い状態になり、一様な結晶粒が得られない場合があった。工業的に使われている「中華鍋方式」は、この点では、粒子の偏析が起こりにくい、合理的なやり方だったのかもしれない。
けれども、これらの問題をクリアすることはそう難しいわけではなく、実験の説明でも述べたように、角の成長の様子は実験パラメータには案外と鈍感である。角が生える条件がうまく達成されると、粒子のサイズや角の本数は、成長を通じて均一化し、それらの分布関数はより鋭い単一のピークを呈するようになる。
では、角が発生するメカニズムについて、我々の実験は何を示唆しているのだろうか。
角は成長の初期には非常に多数(90本程度)の角が生じるが、その間隔は粒子自体の径に比例する。また、同じサイズの種からの成長の様子を追跡すると、成長の後期には、角の間隔は粒子のサイズに比例するように見える(図5)。それに対応して、角の本数は成長とともに自律的に減じられ、定常的な分布に近づいてゆく。つまり、角の特徴的なサイズ(間隔)が粒子そのものの大きさによって決まっている点で、金平糖の成長は結晶成長を含む成長界面の不安定性現象とは本質的に異なると考えられる。
供給したショ糖溶液に含まれるショ糖は、100%金平糖として回収されるので、ショ糖溶液の供給量を変えると、界面の成長速度もそれに応じて調整できる。そして、図5から明らかなように、角の間隔の選択は、ショ糖の供給量(界面の成長率)には依存していない。もし、角の特徴的な長さが、Mullins-Sekerka不安定のように、溶質や潜熱の輸送過程と表面張力による緩和のバランスの上に決まっているとすると、この事実とは明らかに矛盾する。というのは、界面の成長速度は、界面の微小な凹凸の時間発展率に直接影響するため、結晶の析出速度が大きい(拡散長が短い)と、構造の特徴的な長さは短くなるべきだからである。また、樹枝上結晶の先端の放物面の進行速度 v とその特徴的なサイズ(曲率半径)ρの間には v ρ2=const.なる関係が成り立つことも知られている[12]。
金平糖の角の数は粒子のパッキングの状態によって影響されているのでないか。その具体的な根拠はやや不十分ではあるものの、早い時期に福島はすでにこのことを指摘している[2]。
糖蜜をまとった球状の粒子は、攪拌を通じて、周囲の粒子と接触し、糖蜜の授受を行うが、同時にその過程で水の蒸散に伴って、結晶が析出する。表面の液層の厚さは正確に測定してはいないが、供給量と全表面積から考えて、100μm程度以下であろうと我々は推定している。結晶化によって、表面に凹凸が生じると、より突出した部分は、攪拌によって他の粒子と接触する可能性が高くなる。すると、凸部は周囲の粒子から糖蜜が補給されるチャンスが増えるし、また逆に、糖蜜の再分配への寄与も大きいであろう。そして、ある粒子で生じた凹凸の空間的な相関が、周囲の粒子にも伝達される可能性が出てくる。
あるとき実験中に、偶然に(本当はミスで)ショ糖液がドラムの内壁面に直接付着し、そこで結晶化してしまったことがあった。そのとき、すでにドラムの内部には角の生えた粒子が存在していたが、ドラム内壁の結晶にも、金平糖と同様の間隔で角が生えているのが観察された。さらに、もっと積極的に、小さな種粒子から成長させた小さな径の金平糖の中に、その数倍の径の粒子をひとつだけ混入させると、大きな粒子の表面には、小さな粒子と同様の間隔の角が生え始めた。つまり、金平糖の角は、あたかも凸版(あるいは凹版?)印刷のように、周囲の粒子(や壁)にコピーされているように見える。
条件が適切に設定されれば、粒子サイズはほぼ単一の分散のまま成長するので、自分自身と同様な角が生えた粒子同士で、自己触媒的に、角の情報を「プリント」し合うことになるだろう。その際に、ショ糖液は、インクの役割とともに、自らが結晶化することによって、「活字」を形成する役割も演じるはずだ。
こうした金平糖に似た現象として興味深いのは、懸濁電解法によって電解液中から粒子状の金属を回収・精製する際に、粒子の表面に生える角の例である[13]。懸濁電解法では、電解液中で陰極底板の上に多数の金属粒子(粒径1mm程度)を沈めておき、陰極版を振動させることで粒子を攪拌する。その状態で電析を行うと、条件によっては、ニッケルなどの非鉄金属製の「金平糖」が得られるというのだ。無論、細かいメカニズムはショ糖の金平糖とは異なるには違いないが、ここでも粒子の攪拌過程が理解のキーになるのではないだろうか。
最後に、金平糖の表面を覆うショ糖液の「インク」としての役割についてもう少し考察してみたい。印刷に高い粘性を持つインクが用いられるのは、インクが乾くまでの間に流動してしまっては用を成さないからだが、金平糖の作製に濃度の高いショ糖溶液が必要なのも、それをインクに見立てると合点がいく。実験に用いた濃度のショ糖溶液は水に比べて100倍程度以上の粘性率を持つので、インクとしての役割を果たすことができると期待できる。(一方、ショ糖溶液の濃度が低く(例えば 30 wt %以下)粘性が小さい場合、角は生えるものの、金平糖はとてもいびつな形になってしまう。)
結晶の表面を覆う薄い粘性流体の層が存在するとき、層の厚さに不均一があると、気液界面の曲率に応じて発生する表面張力の差に駆動されて、薄膜層はその厚さを一様にすべく、流動しはじめる。このとき、流体の粘度が大きいと、その緩和は時間をかけて進行する。
一方で、高温の雰囲気ゆえに、気液界面からは常に水が蒸発し、その量に応じて、「活字」の部分に相当するショ糖の結晶が析出する。その析出速度は、水の蒸発量に単純に比例すべきであるから、水の蒸散が早い凸部(平均曲率が大きい箇所)では凹部に比べて単位時間あたりの結晶化量も大きいであろう。
簡単のため、平坦な結晶が平均的な厚さ w の流体の薄膜で覆われた状況を想定し、気液界面の高さ h の時間発展を現象論的に考えてみよう[8]。紙数の都合で詳細は割愛するが、系の対称性を考慮し、界面の変形が小さい場合に、最低次の効果のみを取りれると、
![]() (2)
(2)
のように書くことができる。ここで、右辺第一項は凸部の不安定性を、第二項は表面張力による液層の緩和(平坦化)を表す。高粘性領域でその係数は、表面張力σ、粘性係数η、液層の平均の厚みを w を使って、c4=w3σ / 3ηと書かれる。さらに、第三項は平均速度v0 で進展する界面の移動と傾きによる非線形補正を、第四項 ξ(r,t) は粒子どうしの接触と剥離に伴うショ糖液の交換を表す。
これは、外力ξを伴った蔵本・シバシンスキー(KS)方程式に他ならならない[14]。KS方程式で、パラメータ c2, c4に応じた時間・空間的な不安定が生じることはよく調べられているが、長波長領域での系の安定性は中立的で、外力項ξによって生じた凹凸が長時間記憶される効果が期待される。
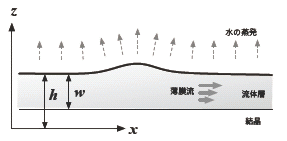 |
図6:ショ糖溶液で覆われた結晶表面を模式的に描いた図。流体層の 不均一は表面張力によって生じる流れによって均一化される一方で、 凸領域では結晶化速度が大きい。 |
これまでの議論が正しいとすれば、問題の核心は、式2の第四項をどのように記述して、閉じた形に問題を定式化するかにあるけれども、流体の層をまとった固体の接触と剥離を記述するだけでもなかなか骨の折れる問題であるし、さらに、多数の粒子が攪拌される様子をどのようにモデル化すべきか、残念ながらこれらについて著者らは良いアイデアをまだ持っていない。
© Yoshinori Hayakawa (2007)