Pygletによる「手抜き」OpenGL入門
10. シェーダーの活用
10.1 ポイントとラインによる星図の表示
天文データベースと恒星の情報
我々の地球は天の川銀河(milky way gallaxy)と呼ばれる星雲の、渦巻き状の構造の「腕」のひとつに位置しており、肉眼で見える星々のほとんどは、同じ「腕」のご近所同士らしい。 その他の遠くの星は、milky wayの名のとおり、点としてではなく、ミルク色の淡い光として認識される。 天文学の進歩によって、こうした天体の精密な計測が可能となり、近隣の星々についてはその空間座標や移動速度等が計測され、カタログ化されている。
そのようなデータベースのうち、比較的コンパクトなHYG databaseのデータをもとに、 地球の周囲の恒星の座標と明るさの情報から、夜空の様子をグラフィックスで再現してみることにしよう。
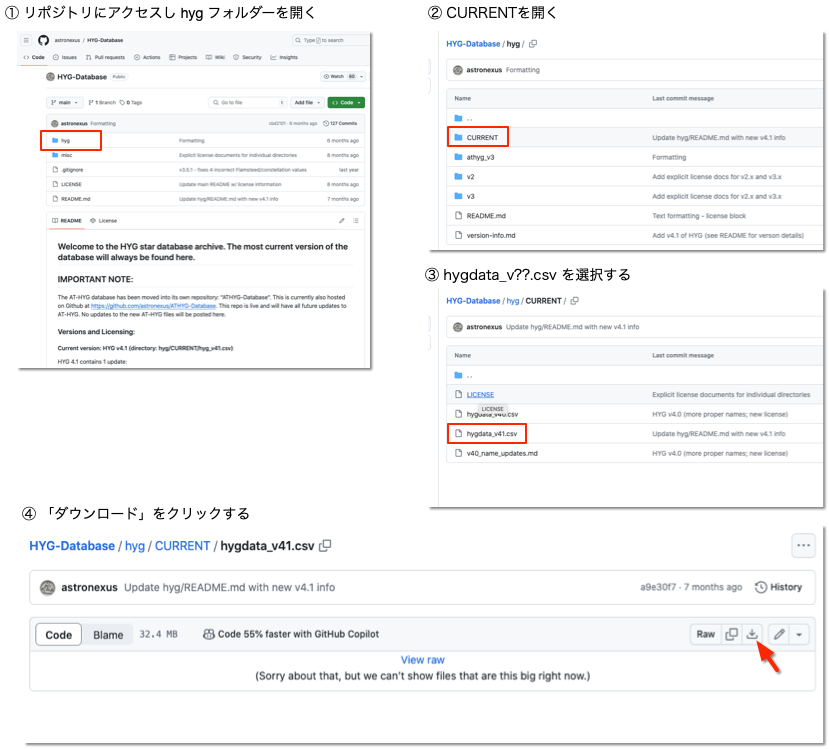
まず、HYGデータベースからCSVファイルをダウンロードする。GitHubのリポジトリを開き、
下図の手順でCSVファイル(hygdata_v[バージョン番号].csv)をダウンロードする。
[バージョン番号]のところは、数字の大きな(新しい)ものを選択すればよい。
データベースには地球から数百パーセク(1パーセクは約3.26光年)程度の距離の範囲内の恒星を中心に、10万パーセクの範囲の恒星約12万弱が登録されている。 データ項目には、地球を原点としたデカルト座標での恒星の位置、恒星の明るさ(絶対等級)、色(B−V色指数)が含まれている。
恒星の座標は 春分点をx座標の正とし、地球の自転軸の方向をz軸、x軸の方向から90度自転した方向をy軸としたデカルト座標で表現されており、CSVデータの x, y, z のカラムにそれぞれ格納されている。 数値の単位はパーセクである。このデータは左手座標系であり、右手座標系のOpenGとの違いを意識する必要がある。
恒星の明るさは絶対等級で表されており、CSVのカラム名はabsmagである。 星の等級は5つ増えると光量が100倍変わるような対数で定義されている。その底を$k$とすれば $\log_k(1/100) = 5$なので、 $-\frac{\log{100}}{\log k} = 5$ すなわち$\log{k} = -\log(100)/5$ で、電卓をはじくと$k = 0.3981 \cdots$となる。 したがって、絶対等級を$m$とすると、星の明るさは $$ k^m = \exp\left( \log(k) \, m\right) = \exp\left( - 0.921 \, m \right) $$ に比例する。
恒星の色は B-V色指数と呼ばれる数値で表現され、CSVのカラム名はciになっている。 B-V指数は、恒星のスペクトルのうち青と紫の相対強度から算出さるような量で、黒体輻射の理論的なスペクトルとを比較することで、表面温度が推定できる。 これは、日常的に使われるようになった赤外放射温度計(二色温度計)の原理と同じである。 B-V指数 $C$ を絶対温度$T$[K]に換算するには、つぎのような近似式が知られている: $$ T = 4600 \left(\frac{1}{0.92 C + 1.7} + \frac{1}{0.92 C + 0.62} \right) $$
しかしながら、表面温度がわかったとしても、それを我々の色覚に合致するよう、光の三原色(RGB)の混合によって表現するのは案外と面倒である。 ここではその詳細には立ち入らず、公開されている変換用のコードを用いることにする。
OpenGLによる可視化
恒星のデータはCSVファイルで入手できるので、pandasを使ってDataFrameオブジェクトに変換後、頂点情報を生成して、GL_POINTSによって描画することにする。 視点(カメラ)の位置は原点(地球)とし、恒星(点)の明るさは絶対等級で決まる明るさに比例し、距離の二乗に反比例するように決める。 ただし、比例係数は試行錯誤によって調整することにする。 また、色指数に応じた点の描画色も頂点情報に加える。
天体写真をじっくる眺めてみると、明るい星は大きなスポット状に写っていることがわかる。 そこで、星の明るさに応じて、点の大きさも調整することにする。 点の大きさは、CPU側のコードで
glEnable(GL_VERTEX_PROGRAM_POINT_SIZE)
を設定しておいてから、頂点シェーダーで組み込み変数 gl_PointSize を設定すればよい。
ただし、点のサイズを大きくすると、点が四角形に描画されて不格好であるので、
床井先生のブログの「点を丸くする」
を参考に、フラグメントシェーダーで加工することにした。
これら、恒星を色とサイズの異なる点として描画するためのシェーダーをまず用意し、Batchオブジェクトの関連づける。
加えて、天球上の座標(赤経と赤緯)の目安とするため、ワイヤーフレームで球を重ね書きすることにする。 そのためのシェーダーも別途用意し、別のBatchオブジェクトと関連づける。
マウスのドラッグで着目点を変えたり、ホィールでのズームイン・アウトが可能となるよう、マウス関連のイベントを定義する共に、 キー操作による視点のリセット(初期位置は春分点(魚座)方向で、上が北)と、方位のリセット(上が北)機能も実装する。
以上の方針に沿ってコーディングしてみた例を prog-10-1.py に示す。
HYGデータベースからダウンロードしたCSVファイルをこのプログラムと同じディレクトリに置き、
最後のあたりの filename = "hygdata_v41.csv" の箇所をダウンロードしたファイル名に書き換えておくこと。
頂点情報の生成に時間を要するため、起動してウィンドウが開くまで、少し待たされるかもしれない。
import numpy as np
import math
import pyglet
from pyglet.gl import *
from pyglet.math import Mat4, Vec3
from pyglet.graphics.shader import Shader, ShaderProgram
import pandas as pd
# 星の表示用シェーダー
vertex_source_0 = """#version 330 core
in vec3 position;
in vec4 colors;
in float absmags;
out vec4 vertex_colors;
out vec3 vertex_position;
out float vertex_brightness;
uniform WindowBlock
{
mat4 projection;
mat4 view;
} window;
uniform mat4 model;
#define BFACT 4000
void main()
{
mat4 modelview = window.view * model;
vec4 pos = modelview * vec4(position, 1.0);
gl_Position = window.projection * pos;
float dist = distance(vec3(0.0, 0.0, 0.0), pos.xyz) ;
float brightness = exp(-absmags*0.921) / (dist*dist) * BFACT ;
gl_PointSize = log(brightness+1.0)+2.0 ;
if (brightness>1.0) brightness=1.0 ;
vertex_position = pos.xyz;
vertex_colors = colors;
vertex_brightness = brightness;
}
"""
fragment_source_0 = """#version 330 core
in vec4 vertex_colors;
in vec3 vertex_position;
in float vertex_brightness;
out vec4 final_colors;
void main()
{
vec2 pos = gl_PointCoord * 2.0 - 1.0;
float r = 1.0 - dot(pos, pos);
if (r < 0.0) discard;
final_colors = vertex_colors * vertex_brightness ;
}
"""
# ワイヤーフレーム表示用シェーダー
vertex_source_1 = """#version 330 core
in vec3 position;
in vec4 colors;
out vec4 vertex_colors;
out vec3 vertex_position;
uniform WindowBlock
{
mat4 projection;
mat4 view;
} window;
uniform mat4 model;
void main()
{
mat4 modelview = window.view * model;
vec4 pos = modelview * vec4(position, 1.0);
gl_Position = window.projection * pos;
vertex_position = pos.xyz;
vertex_colors = colors;
}
"""
fragment_source_1 = """#version 330 core
in vec4 vertex_colors;
in vec3 vertex_position;
out vec4 final_colors;
void main()
{
final_colors = vertex_colors ;
}
"""
window = pyglet.window.Window(width=1280, height=720, resizable=True)
window.set_caption('Star map')
# シェーダーのコンパイル
batch0 = pyglet.graphics.Batch()
vert_shader_0 = Shader(vertex_source_0, 'vertex')
frag_shader_0 = Shader(fragment_source_0, 'fragment')
shader0 = ShaderProgram(vert_shader_0, frag_shader_0)
batch1 = pyglet.graphics.Batch()
vert_shader_1 = Shader(vertex_source_1, 'vertex')
frag_shader_1 = Shader(fragment_source_1, 'fragment')
shader1 = ShaderProgram(vert_shader_1, frag_shader_1)
@window.event
def on_draw():
window.clear()
shader0['model']=Mat4()
shader1['model']=Mat4() # 赤道座標グリッド
batch1.draw()
batch0.draw()
fov = 60
@window.event
def on_resize(width, height):
window.viewport = (0, 0, width, height)
ratio = width/height
window.projection = Mat4.perspective_projection(window.aspect_ratio, z_near=0.01, z_far=100000, fov=fov)
return pyglet.event.EVENT_HANDLED
@window.event
def on_mouse_scroll(x, y, scroll_x, scroll_y):
global fov
fov += scroll_y
if fov < 1:
fov = 1
elif fov>90:
fov = 90
window.projection = Mat4.perspective_projection(window.aspect_ratio, z_near=0.01, z_far=10000, fov=fov)
return pyglet.event.EVENT_HANDLED
@window.event
def on_mouse_drag(x,y,dx,dy,buttons,modifiers):
global view_matrix
view_matrix = Mat4.from_rotation(-dx*0.005, Vec3(0, 1, 0)) @ view_matrix
view_matrix = Mat4.from_rotation(dy*0.005, Vec3(1, 0, 0)) @ view_matrix
window.view = view_matrix
return pyglet.event.EVENT_HANDLED
@window.event
def on_key_press(symbol, modifiers):
global view_matrix
if symbol == pyglet.window.key.R:
view_matrix = Mat4.look_at(position=Vec3(0,0,0), target=Vec3(100000,0,0), up=Vec3(0,1,0))
window.view = view_matrix
elif symbol == pyglet.window.key.U:
d = view_matrix.row(2)
view_matrix = Mat4.look_at(position=Vec3(0,0,0), target=Vec3(-d[0]*100000,-d[1]*100000,-d[2]*100000), up=Vec3(0,1,0))
window.view = view_matrix
return pyglet.event.EVENT_HANDLED
def setup():
glClearColor(0.01, 0.01, 0.05, 1.0)
glEnable(GL_VERTEX_PROGRAM_POINT_SIZE)
on_resize(*window.size)
###
# this part was taken from the answer by DocLeonard in
# https://stackoverflow.com/questions/21977786/star-b-v-color-index-to-apparent-rgb-color
redco = [ 1.62098281e-82, -5.03110845e-77, 6.66758278e-72, -4.71441850e-67, 1.66429493e-62, -1.50701672e-59, -2.42533006e-53,
8.42586475e-49, 7.94816523e-45, -1.68655179e-39, 7.25404556e-35, -1.85559350e-30, 3.23793430e-26, -4.00670131e-22,
3.53445102e-18, -2.19200432e-14, 9.27939743e-11, -2.56131914e-07, 4.29917840e-04, -3.88866019e-01, 3.97307766e+02]
greenco = [ 1.21775217e-82, -3.79265302e-77, 5.04300808e-72, -3.57741292e-67, 1.26763387e-62, -1.28724846e-59, -1.84618419e-53,
6.43113038e-49, 6.05135293e-45, -1.28642374e-39, 5.52273817e-35, -1.40682723e-30, 2.43659251e-26, -2.97762151e-22,
2.57295370e-18, -1.54137817e-14, 6.14141996e-11, -1.50922703e-07, 1.90667190e-04, -1.23973583e-02,-1.33464366e+01]
blueco = [ 2.17374683e-82, -6.82574350e-77, 9.17262316e-72, -6.60390151e-67, 2.40324203e-62, -5.77694976e-59, -3.42234361e-53,
1.26662864e-48, 8.75794575e-45, -2.45089758e-39, 1.10698770e-34, -2.95752654e-30, 5.41656027e-26, -7.10396545e-22,
6.74083578e-18, -4.59335728e-14, 2.20051751e-10, -7.14068799e-07, 1.46622559e-03, -1.60740964e+00, 6.85200095e+02]
redco = np.poly1d(redco)
greenco = np.poly1d(greenco)
blueco = np.poly1d(blueco)
def temp2rgb(temp):
red = redco(temp)
green = greenco(temp)
blue = blueco(temp)
if red > 255:
red = 255
elif red < 0:
red = 0
if green > 255:
green = 255
elif green < 0:
green = 0
if blue > 255:
blue = 255
elif blue < 0:
blue = 0
return (red/255, green/255, blue/255)
###
def bv2rgb(bv):
t = 4600*(1/(0.92*bv + 1.7) + 1/(0.92*bv+0.62))
r,g,b = temp2rgb(t)
return (r,g,b)
def gen_stars(filename, shader, batch):
print("reading",filename)
df = pd.read_csv(filename)
print("generating vertecies...")
vertices = []
absmags = []
colors = []
for index, row in df.iterrows():
vertices.extend([row['x'],row['z'],-row['y']])
absmags.append(row['absmag'])
if row['ci']:
r,g,b = bv2rgb(row['ci'])
colors.extend([r,g,b,1.0])
else:
colors.extend([0,0,0,0])
vertex_list = shader.vertex_list(len(vertices)//3, GL_POINTS, batch=batch)
vertex_list.position[:] = vertices
vertex_list.absmags[:] = absmags
vertex_list.colors[:] = colors
return vertex_list
def gen_sphere(radius,stacks,slices,shader, batch):
vertices = []
for i in range(stacks + 1):
phi = math.pi / 2 - i * math.pi / stacks
y = radius * math.sin(phi)
r = radius * math.cos(phi)
for j in range(slices + 1):
theta = j * 2 * math.pi / slices
x = r * math.cos(theta)
z = r * math.sin(theta)
vertices.extend([x, y, z])
indices = []
for i in range(stacks):
for j in range(slices):
p1 = i * (slices+1) + j
p2 = p1 + (slices+1)
indices.extend([p1, p2])
indices.extend([p1, p1+1])
vertex_list = shader.vertex_list_indexed(len(vertices)//3, GL_LINES, indices, batch=batch,
position=('f', vertices),
colors =('f', [0.15,0.15,0.2,1]*(len(vertices)//3)))
return vertex_list
# OpenGLの初期設定
setup()
# CSV
filename = "hygdata_v41.csv"
vertex_list0 = gen_stars(filename,shader0,batch0)
vertex_list1 = gen_sphere(100,12,24,shader1,batch1)
# 視点を設定
view_matrix = Mat4.look_at(position=Vec3(0,0,0), target=Vec3(100000,0,0), up=Vec3(0,1,0))
window.view = view_matrix
pyglet.app.run()
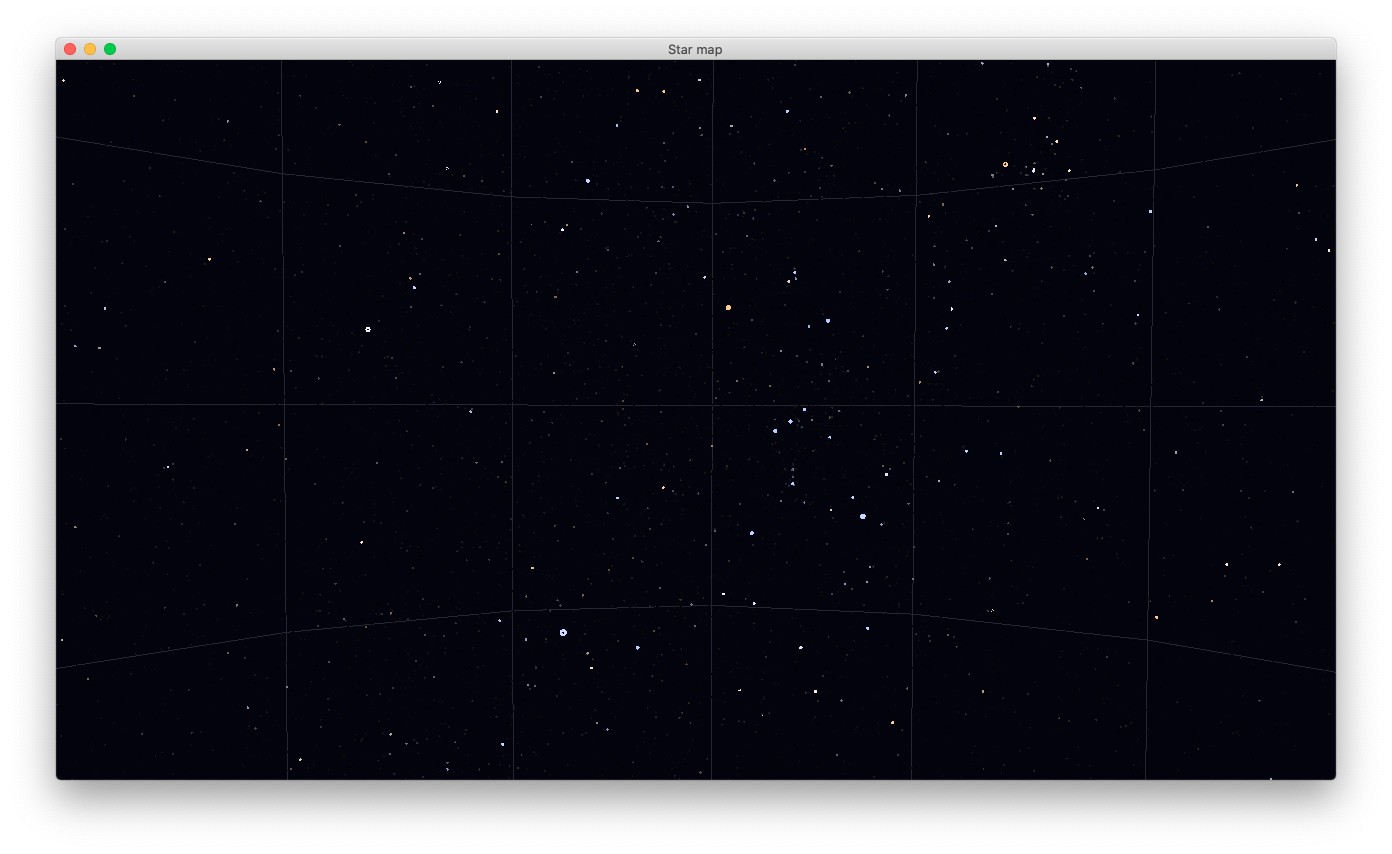
prog-10-1.pyのスクリーンショット。オリオン座の辺りを表示している。 Rキーで視点のリセット、Uキーで上を北極方向に回転、マウスのドラッグで回転、ホィールでズーミングが可能。 メッシュは1つあたり15度(1H)に相当。
 練習
練習
もし地球の位置が異なっていたら、星の配置はどれくらい異なって見えるものか、シミュレーションしてみなさい。
恒星の明るさは距離の二乗に反比例するが、もし距離に反比例、あるいは、別の法則に従っていたとすると、星空の見え方はどれくらい違うか、シミュレーションしてみなさい。

10.2 ジオメトリ・シェーダーを使った太さのある線分の表示
ジオメトリ・シェーダー
OpenGLの標準的な線分描画では不十分で、「太さ」のある線を描きたいことがたまにある。 そのような場合、細長い円柱として線分を表現するのが一般的である。
そこで、GL_LINESやGL_LINE_STRIPのプリミティブを与えると、自動的に太さのある線分(管?)が生成されるよう、シェーダーを構成してみることにしよう。
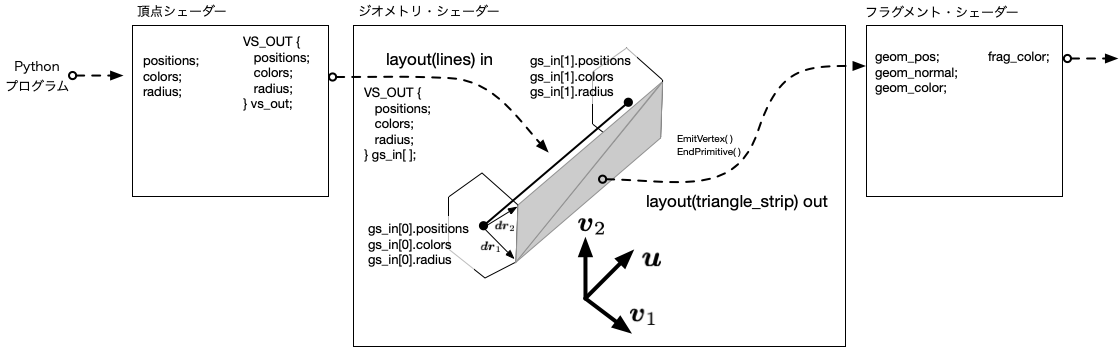
ここまでの例では、シェーダーは頂点シェーダーとフラグメント・シェーダーの二段階で構成していたが、 その中間にジオメトリ・シェーダーと呼ばれるシェーダーを配置することができる。 ジオメトリ・シェーダーは、頂点シェーダーからプリミティブ(点、線、三角形など)についての情報を受け取り、それを操作したり、新しいプリミティブを生成するために用いる。 この節のケースでは、線分の頂点情報を頂点シェーダーから受け取り、それをもとに、円柱を構成する複数の三角形をフラグメント・シェーダーに出力するようにするわけである。
ジオメトリ・シェーダーの大まかな処理の流れは、以下のとおりである。
- ジオメトリ・シェーダーの冒頭には layout 修飾子を置くルールになっていて、どの種類のプリミティブを受取り、どんなプリミティブを次段に渡すかを示しておく。
- 前段の頂点シェーダーからは、入力するプリミティブの種類によって、必要な数の頂点情報が配列として渡される。
- それらを処理して、新たな頂点を生成し、組み込み関数 EmitVertex(), EndPrimitive()を呼び出しながら、フラグメント・シェーダー側にデータを送る。
線分から円筒(もどき)を生成するため、まず、線分の方向ベクトル $\boldsymbol{u}$に直交する2つの単位ベクトル $\boldsymbol{v}_1,\; \boldsymbol{v}_2$ を求めておく。 これらを基底として使いつつ、$\boldsymbol{u}$に直交し線分の端点を含むようなふたつの平面内で、それぞれ正多角形を構成し、その頂点座標を使って 円筒の側面を構成する三角形を順次生成する(上図を参照)。
これら実装し、三次元中のランダムウォークの軌跡をロッドの集まりのようにして描画させてみたのが、以下である。
# Vertex shader
vertex_source = """#version 330 core
in vec3 positions;
in vec4 colors;
in float radius;
out VS_OUT {
vec3 positions;
vec4 colors;
float radius;
} vs_out;
void main()
{
vs_out.positions = positions;
vs_out.colors = colors ;
vs_out.radius = radius ;
}
"""
# Geometory shader
geometry_source = """#version 330 core
layout(lines) in;
layout(triangle_strip, max_vertices = 200) out;
in VS_OUT {
vec3 positions;
vec4 colors;
float radius;
} gs_in[];
out vec3 geom_pos;
out vec3 geom_normal;
out vec4 geom_color;
uniform mat4 model;
uniform WindowBlock
{
mat4 projection;
mat4 view;
} window;
#define N 6
#define TWO_PI 6.28318530718
void main()
{
mat4 modelview = window.view * model ;
mat3 normal_matrix = transpose(inverse(mat3(modelview)));
vec4 world_position ;
vec4 view_position ;
vec3 pos1 = gs_in[0].positions;
float r1 = gs_in[0].radius;
vec4 color1 = gs_in[0].colors;
vec3 pos2 = gs_in[1].positions;
float r2 = gs_in[1].radius;
vec4 color2 = gs_in[1].colors;
vec3 u = normalize(pos2 - pos1) ;
vec3 v1,v2 ;
if (abs(u.z - 1) > 1e-6) {
v1 = normalize(vec3(u.y, -u.x, 0)) ;
v2 = cross(u,v1) ;
} else {
v1 = vec3(1,0,0) ;
v2 = vec3(0,1,0) ;
}
for (int i=0; i<N; i++) {
float angle1 = TWO_PI * i/N ;
float angle2 = TWO_PI * (i+1)/N;
vec3 dr1 = cos(angle1) * v1 + sin(angle1) * v2;
vec3 dr2 = cos(angle2) * v1 + sin(angle2) * v2;
// Triangle 1
world_position = vec4(pos1+dr1*r1, 1.0) ;
view_position = modelview * world_position ;
gl_Position = window.projection * view_position ;
geom_pos = view_position.xyz;
geom_normal = normal_matrix * dr1 ;
geom_color = color1 ;
EmitVertex();
world_position = vec4(pos1+dr2*r1, 1.0) ;
view_position = modelview * world_position ;
gl_Position = window.projection * view_position ;
geom_pos = view_position.xyz;
geom_normal = normal_matrix * dr2 ;
geom_color = color1 ;
EmitVertex();
world_position = vec4(pos2+dr2*r2, 1.0) ;
view_position = modelview * world_position ;
gl_Position = window.projection * view_position ;
geom_pos = view_position.xyz;
geom_normal = normal_matrix * dr2 ;
geom_color = color2 ;
EmitVertex();
EndPrimitive();
// Triangle 2
world_position = vec4(pos1+dr1*r1, 1.0) ;
view_position = modelview * world_position ;
gl_Position = window.projection * view_position ;
geom_pos = view_position.xyz;
geom_normal = normal_matrix * dr1 ;
geom_color = color1 ;
EmitVertex();
world_position = vec4(pos2+dr2*r2, 1.0) ;
view_position = modelview * world_position ;
gl_Position = window.projection * view_position ;
geom_pos = view_position.xyz;
geom_normal = normal_matrix * dr2 ;
geom_color = color2 ;
EmitVertex();
world_position = vec4(pos2+dr1*r2, 1.0) ;
view_position = modelview * world_position ;
gl_Position = window.projection * view_position ;
geom_pos = view_position.xyz;
geom_normal = normal_matrix * dr1 ;
geom_color = color2 ;
EmitVertex();
EndPrimitive();
}
}
"""
# Fragment shader
fragment_source = """#version 330 core
in vec3 geom_pos;
in vec3 geom_normal;
in vec4 geom_color;
out vec4 frag_color;
uniform vec3 light_position ;
void main()
{
vec3 normal = normalize(geom_normal);
vec3 light_dir = normalize(light_position - geom_pos);
float diff = max(dot(normal, light_dir), 0.0);
frag_color = geom_color * diff ;
}
"""
import numpy as np
import pyglet
from pyglet.gl import *
from pyglet.math import Mat4, Vec3
from pyglet.graphics.shader import Shader, ShaderProgram
window = pyglet.window.Window(width=1280, height=720, resizable=True)
@window.event
def on_draw():
window.clear()
shader['light_position'] = Vec3(50,200,200)
batch.draw()
@window.event
def on_resize(width, height):
window.viewport = (0, 0, width, height)
window.projection = Mat4.perspective_projection(window.aspect_ratio, z_near=0.1, z_far=255, fov=60)
return pyglet.event.EVENT_HANDLED
def update(dt):
global time
time += dt
rot_x = Mat4.from_rotation(time/3, Vec3(1, 0, 0))
rot_y = Mat4.from_rotation(time/7, Vec3(0, 1, 0))
rot_z = Mat4.from_rotation(time/11, Vec3(0, 0, 1))
trans = Mat4.from_translation(Vec3(0, 0, 0))
shader['model'] = trans @ rot_z @ rot_y @ rot_x ;
def setup():
# One-time GL setup
glClearColor(0.2, 0.2, 0.3, 1)
glEnable(GL_DEPTH_TEST)
on_resize(*window.size)
# Uncomment this line for a wireframe view:
# glPolygonMode(GL_FRONT_AND_BACK, GL_LINE)
setup()
time = 0.0
batch = pyglet.graphics.Batch()
group = pyglet.graphics.Group(order=0)
vert_shader = Shader(vertex_source, 'vertex')
geom_shader = Shader(geometry_source, 'geometry')
frag_shader = Shader(fragment_source, 'fragment')
shader = ShaderProgram(vert_shader, geom_shader, frag_shader)
vertices = [ ]
x = 0
y = 0
z = 0
for i in range(2000):
vertices.extend([x,y,z])
x += np.random.normal(loc=0,scale=1)
y += np.random.normal(loc=0,scale=1)
z += np.random.normal(loc=0,scale=1)
lines = shader.vertex_list(len(vertices)//3, GL_LINE_STRIP,
positions=('f', vertices),
colors = ('f', [1.0, 0.0, 0.0, 1.0] * (len(vertices)//3)),
radius = ('f', [0.15]*(len(vertices)//3)),
batch=batch)
window.view = Mat4.look_at(position=Vec3(0,0,25), target=Vec3(0,0,0), up=Vec3(0,1,0))
pyglet.clock.schedule_interval(update, 1/60)
pyglet.app.run()
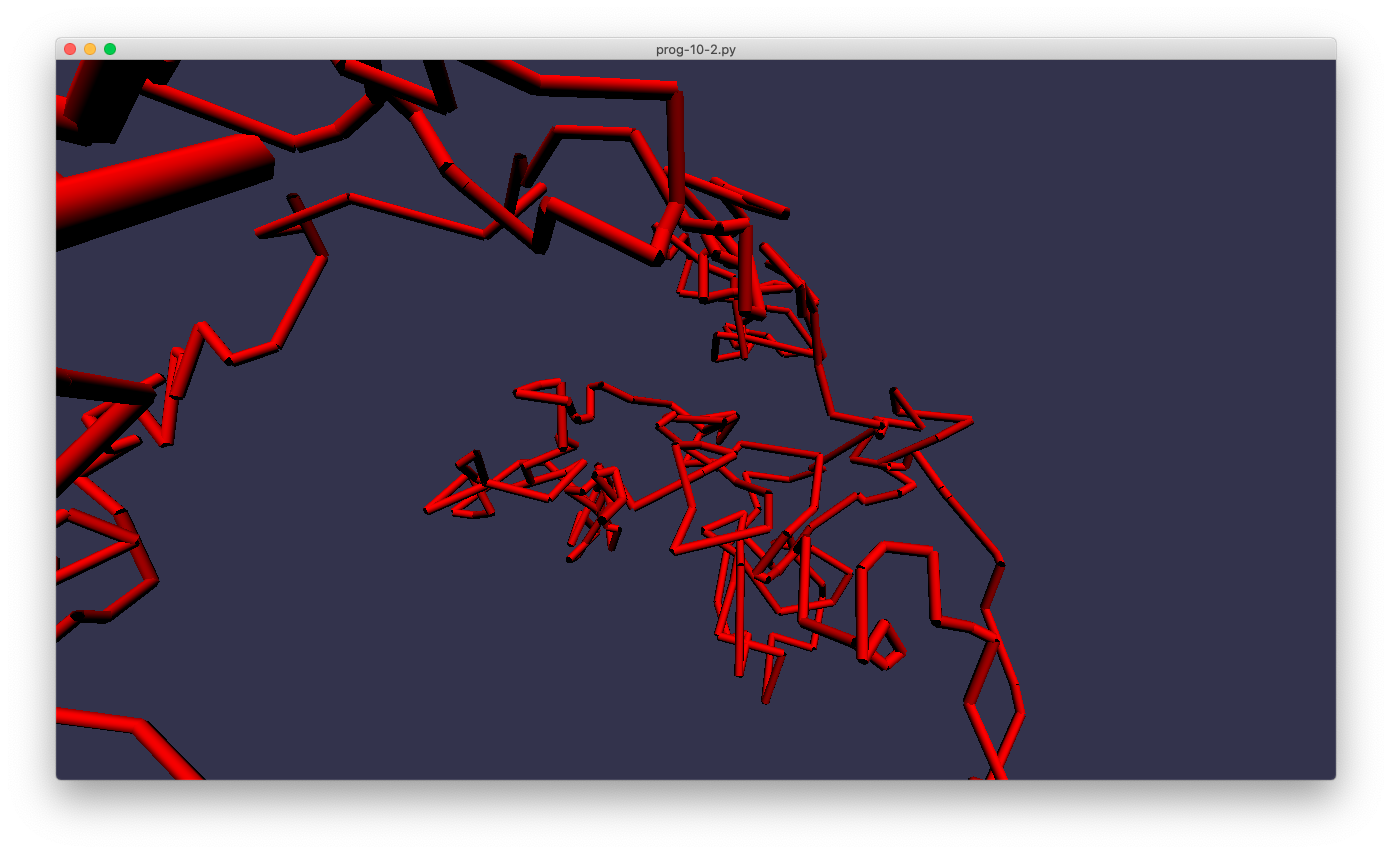
prog-10-2.pyの実行中の様子
表示結果を見ると、実際に描画しているのは、円柱ではなく六角柱であるのに、影のつき方は案外と滑らかに見える。 これは、このコードでは法線ベクトルを(三角形の法線ではなくて)円の動径方向に設定してるからである。 ジオメトリ・シェーダーから受け取った法線ベクトルを使って、頂点以外での法線をフラグメント・シェーダーが自動的に補間してくれるため、スムースに見えているわけである。
 練習
練習
ジオメトリ・シェーダーに手を加え、円筒の両端が閉じるよう「キャップ」をつけてみなさい。

10.3 コンピュート・シェーダーを使ったセルラー・オートマトンの計算
計算専用のシェーダー
OpenGL バージョン 4.3以上には、GPUの演算機能を利用するための新しい機能として、コンピュート・シェーダーが追加された。 このセクションでは、セルラー・オートマトンの計算を、 コンピュート・シェダーを使って高速化する実験をしてみよう。 なお、パソコンによってはOpenGLのバージョンが古く、以下の例を実行しようとすると
pyglet.graphics.shader.ShaderException: Compute Shader not supported. OpenGL Context version must be at least 4.3 or higher, or 4.2 with the 'GL_ARB_compute_shader' extension.
というエラーで停止する場合がある。そんな場合、もし可能なら、比較的新しい WindowsかLinuxのパソコンで試してみるとよい。
OpenGL 4.2に対応し、かつGL_ARB_compute_shader拡張機能が有効な場合は、コンピュート・シェーダーの冒頭部分 #version 430 core を
#version 420 #extension GL_ARB_compute_shader : require
に変更し、かつ、main()関数中の変数 img_size の定義部分を以下のように変更することで、本節の例題プログラムは実行可能(なはず)である。
ivec2 img_size = ivec2(1024,1024) ;
ここで、1024のところは、Pythonコードのwidth と height に合わせておくこと。
シェーダーによるGPU計算
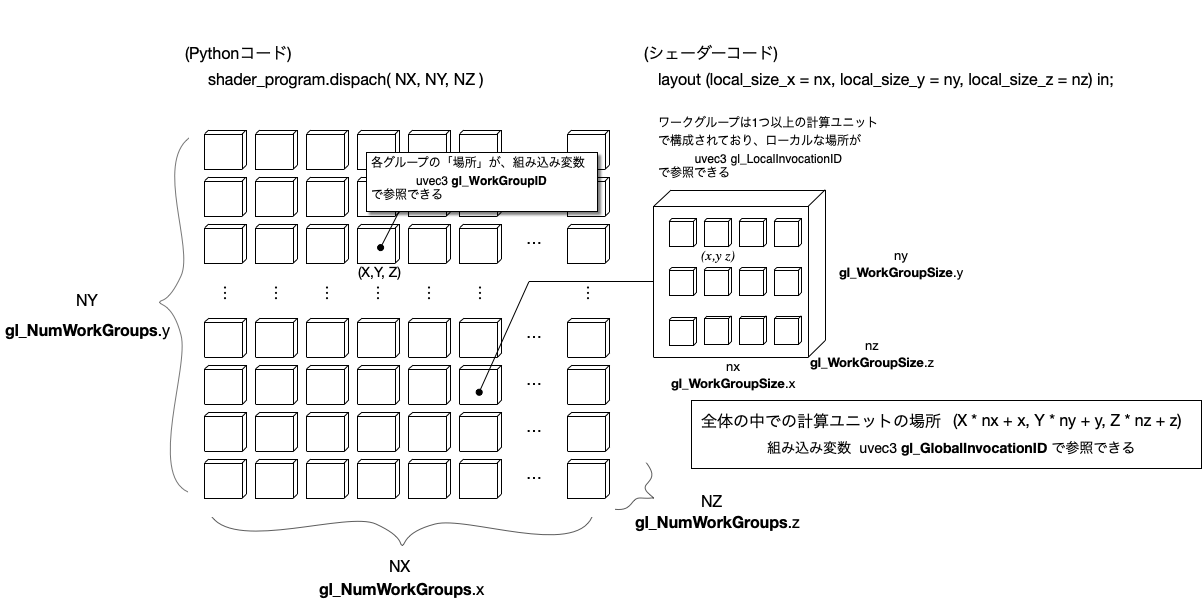
GPUは沢山の演算装置の集合体で、それらを並列動作させることで、全体として大きな処理速度の向上が見込める。 OpenGLのコンピュート・シェダーは、演算装置を三次元的に配置したような論理構造で設計されている。 演算装置のひとまとまりをワークグループと呼び、それぞれのワークグループ内に複数の演算装置(以下ではワーカーと呼ぶことにする。実際には、GPUで実行されるスレッドに対応。)を配置するような、二段階(二階層)になっている。 パソコンが縦横上下に積み上げられ、それぞれのパソコンに複数のコアが内蔵されている、そんなイメージである。
ワークグループのサイズを確認するためのスクリプト: check-local-size.py
ワークグループサイズはシェーダーのコードに静的に指定しなければならないので、計算の規模に応じた自動調整などはできない。
ワークグループ内のワーカー(スレッド)は、相互に通信が可能で、barrier()関数やgroupMemoryBarrier()関数を使って同期を取る手段が提供されている。
一方、異なるワークグループのワーカー同士が直接的に同期を取る手段は提供されていない。 ワークグループの個数は起動(ディスパッチ)の際に調整できるようになっている。
ここでは、Conwayのライフゲームを例に、セルをひとつの演算装置に対応させ、セルのアップデートを並列処理してみることにしよう。 まず、二次元正方格子状に配列しているセルを、シェーダーのワークグループに対応させる。 ここでは、ワークグループ毎のローカルな演算装置は1つだけとする。 そして、Z方向(奥行き方向)には1層だけにしておけば、全体として、セルとワーカーがきれいに対応する。 ローカルなワーカーを1つだけにするには、シェーダーに、
layout (local_size_x = 1, local_size_y = 1, local_size_z = 1) in;
と記述する。x, y, z方向のサイズがそれぞれ1なので、$1 \times 1 \times 1 = 1$個のローカルな演算装置を割り当てることになる。
それぞれのローカルなワーカーは、セルの状態を表すデータをテクスチャー画像として入力し、更新結果をテクスチャー画像として出力するよう設計してみよう。
ライフゲームでは、セルの状態は0と1の2状態のみ(すなわち1ビット)である一方、ここでは無駄は承知で、RGBAの画像(シェーダー内ではrgba32fと表記)と対応づけることにする。
具体的には、赤のピクセル値の 0 か 1 かで、オートマトンの各セルの状態を表現する。
テクスチャーの入出力のため、シェーダーでは
layout(rgba32f,binding=0) uniform image2D image_data; layout(rgba32f,binding=1) uniform image2D image_out;
のようにuniform変数を宣言しておく。そして、Pythonコードからテクスチャーのユニット番号を指定しながら、テクスチャーをバインドする。
この例では、image_dataをユニット番号0、image_outをユニット番号1にバインドすると宣言していることになる。
格子状に配置されたGPUの演算装置では、全く同じコードが実行される(Single Instruction, Multiple Data; SIMD方式な)ので、各ワーカーが自分がどのセルを担当しているのかを知る必要がある。
シェーダーの組み込み変数 gl_GlobalInvocationID には、そのワーカーの「位置」に相当する三次元座標があらかじめセットされているので、
それを元に、該当するデータ(テクスチャ画像の画素)の処理を行えばよい。
ivec2 c_coord = ivec2(gl_GlobalInvocationID.xy); vec4 center = imageLoad(image_data, c_coord);
の2行で、変数c_coordにワーカーの座標(すなわち、担当するピクセルの位置)をセットし、
テクスチャー画像から当該のピクセル値(RGBA)を変数 center に読み込むことができる。
セルラー・オートマトンの計算に実数を用いる必要は無いので、layout(rgba8ui) uniform uimage2D ...
のように宣言して、符号なし整数で受け渡すほうが合理的かもしれないが、現状のPygletでは、rgba8uiを使おうとすると
エラーになるようである。
なお、rgba8でデータを受け渡す場合は、imageLoad()の際に0から255の整数が自動的に0から1の実数に変換されるので、
シェーダー内での計算は実数で行うことになる。
詳しくはこちらも参照のこと。
同様に、周囲の8つの近傍のピクセル値も読み出した上で、ライフゲームのルールに従って、出力用のテクスチャーの画素への書き込みを
float sum = left.r + right.r + top.r + bottom.r + top_right.r
+ top_left.r + bottom_right.r + bottom_left.r ;
if (sum==3) {
value.r = 1 ;
} else if (center.r==1 && sum==2) {
value.r = 1 ;
} else {
value.r = 0 ;
}
imageStore(image_out, c_coord, value);
のように行う。
受け持っている座標c_coordにだけ、値valueを書き込むので、他のワーカーと干渉や衝突が起きる心配はない。
データの受け渡しとシェーダーの起動
Python(CPU)側では、シェーダーを
program = pyglet.graphics.shader.ComputeShaderProgram(compute_src)
によってコンパイルし、ShaderProgramのオブジェクト(program)を生成する。
次いで、シェーダーとのデータのやりとりに用いる2つのテクスチャーを作成し、シェーダーとバインドしておく:
img_array = init_array.reshape((height, width, 4))
glActiveTexture(GL_TEXTURE0)
texture0 = pyglet.image.Texture.create(width, height, internalformat=GL_RGBA32F)
texture0.bind_image_texture(unit=0,fmt=GL_RGBA32F)
glTexImage2D(pyglet.gl.GL_TEXTURE_2D, 0, GL_RGBA32F, width, height, 0,
GL_RGBA, GL_FLOAT, img_array.ctypes.data)
texture1 = pyglet.image.Texture.create(texture0.width, texture0.height, internalformat=GL_RGBA32F)
glActiveTexture(GL_TEXTURE1)
texture1.bind_image_texture(unit=1,fmt=GL_RGBA32F)
ここで、texture0は入力用で、あらかじめ乱数で生成した配列(init_array)に値を設定しておく。
一方、texture1は結果の出力用である。
各セルの計算が並列的に進むため、同じメモリに読み書きすると整合性が維持できないため、同期的な更新が必要なライフゲームの計算では、このように入力と出力を分けておく必要がある。
コンピュート・シェーダーは、画面描画の都度 on_draw()関数の中から
with program:
program.dispatch(texture0.width, texture0.height, 1)
によって起動する。ワーカーグループの個数はX軸方向がtexture0.width、Y軸がtexture0.height、Z軸方向が1で、
これはテクスチャーの画素と対応する。
1ステップ分の更新が終了したら、出力用のテクスチャーを画像としてウィンドウに表示する。その方法はとてもシンプルで
texture1.blit(0, 0)
で事足りる。
最後に、セルラー・オートマトンの次の更新ステップに進むため、出力用テクスチャーの内容を入力用テクスチャーに書き戻しておく。 こちらも、
texture0.blit_into(texture1.get_image_data(),0,0,0)
のようにtexture1からtexture0に画像をコピーするだけである
(blit()は画像をフレームバッファへコピー、blit_into()は画像間でコピー)。
以上の動作をクロックを使って反復することによって、セル全体が次々と更新されることになる。
これらの断片をまとめたコードの全体が以下のとおりである:
import pyglet
from pyglet.gl import *
import numpy as np
import random
print(gl_info.get_version())
print(gl_info.get_vendor())
print(gl_info.get_renderer())
# print(gl_info.get_extensions())
compute_src = """#version 430 core
layout (local_size_x = 1, local_size_y = 1, local_size_z = 1) in;
layout(rgba32f,binding=0) uniform image2D image_data;
layout(rgba32f,binding=1) uniform image2D image_out;
ivec2 coord(ivec2 center, ivec2 size, int dx, int dy) {
return ivec2((center.x + dx + size.x) % size.x, (center.y + dy + size.y) % size.y) ;
}
void main() {
vec4 value = vec4(0, 0.05, 0.15, 1);
ivec2 img_size = imageSize(image_data) ;
ivec2 c_coord = ivec2(gl_GlobalInvocationID.xy);
vec4 center = imageLoad(image_data, c_coord);
ivec2 r_coord = coord(c_coord, img_size, +1, 0) ;
ivec2 l_coord = coord(c_coord, img_size, -1, 0) ;
ivec2 t_coord = coord(c_coord, img_size, 0, +1) ;
ivec2 b_coord = coord(c_coord, img_size, 0, -1) ;
ivec2 tr_coord = coord(c_coord, img_size, +1, +1) ;
ivec2 tl_coord = coord(c_coord, img_size, -1, +1) ;
ivec2 br_coord = coord(c_coord, img_size, +1, -1) ;
ivec2 bl_coord = coord(c_coord, img_size, -1, -1) ;
vec4 left = imageLoad(image_data, l_coord);
vec4 right = imageLoad(image_data, r_coord);
vec4 top = imageLoad(image_data, t_coord);
vec4 bottom = imageLoad(image_data, b_coord);
vec4 top_right = imageLoad(image_data, tr_coord);
vec4 top_left = imageLoad(image_data, tl_coord);
vec4 bottom_right = imageLoad(image_data, br_coord);
vec4 bottom_left = imageLoad(image_data, bl_coord);
float sum = left.r + right.r + top.r + bottom.r + top_right.r + top_left.r + bottom_right.r + bottom_left.r ;
if (sum==3) {
value.r = 1 ;
} else if (center.r==1 && sum==2) {
value.r = 1 ;
} else {
value.r = 0 ;
}
imageStore(image_out, c_coord, value);
}
"""
width=1024
height=1024
window = pyglet.window.Window(width=width, height=height, resizable=False)
window.set_caption('Game of life')
init_array = np.empty((height, width, 4), dtype=np.float32)
for i in range(height):
for j in range(width):
init_array[i,j,0] = random.choice([0.0, 1.0])
init_array[i,j,1] = 0
init_array[i,j,2] = 0
init_array[i,j,3] = 1.0
program = pyglet.graphics.shader.ComputeShaderProgram(compute_src)
img_array = init_array.reshape((height, width, 4))
glActiveTexture(GL_TEXTURE0)
texture0 = pyglet.image.Texture.create(width, height, internalformat=GL_RGBA32F)
texture0.bind_image_texture(unit=0,fmt=GL_RGBA32F)
glTexImage2D(pyglet.gl.GL_TEXTURE_2D, 0, GL_RGBA32F, width, height, 0,
GL_RGBA, GL_FLOAT, img_array.ctypes.data)
texture1 = pyglet.image.Texture.create(texture0.width, texture0.height, internalformat=GL_RGBA32F)
glActiveTexture(GL_TEXTURE1)
texture1.bind_image_texture(unit=1,fmt=GL_RGBA32F)
default_shader = pyglet.graphics.get_default_blit_shader()
loop_cnt=0
label = pyglet.text.Label('GENERATION =' + str(loop_cnt),
font_name='Arial', color=(200, 200, 200, 128),
font_size=14, x=10, y=10,
anchor_x='left', anchor_y='bottom')
def rotate():
global loop_cnt
texture0.blit_into(texture1.get_image_data(),0,0,0)
loop_cnt += 1
def update(dt):
rotate()
label.text = 'GENERATION =' + str(loop_cnt)
@window.event
def on_draw():
program.use()
with program:
program.dispatch(texture0.width, texture0.height, 1)
program.stop()
window.clear()
default_shader.use()
texture1.blit(0, 0)
label.draw()
pyglet.clock.schedule_interval(update,1/30)
pyglet.app.run()
prog-10-3.pyによる表示画面のスナップショット。$1024 \times 1024$の各ピクセルがそれぞれのセルに対応している。