Pythonプログラミング(その他のトピック・セル・オートマトン)
このページでは、時々刻々と状態が変化するような問題の可視化方法の例として、 複雑な現象の数理モデル化等に用いられるセル・オートマトンのシミュレーションを試してみる(ここはこれから)
一次元のセル・オートマトン
万物は、自らとその周りの状態に応じて変化している、と言っても差し支えないだろう。 ここで、「自ら」とは、生物の細胞であったり、ある場所の気象であったり、コンピュータであったり、AIであったりと様々であろうし、 「その周り」をどう定義するかもまた多様である。
ここでは、具体的な事象から少し距離を置いて、そのような系を究極的に単純化した以下のようなモデルを考えてみる。 まず、マス目に区切られた空間の一区画(セル)を考え、それを「自分」とみなす。 自分の状態は、0と1、あるいは数種類程度の数値で表現できるとする。 時間もまた離散的に進行し、隣り合う区画(近傍のセル)の状態(数値)と自らの状態に応じて、次の時間ステップの自分の状態が決まる。
一次元の配列(リスト)を考え、0と1がセットされている。 $i$番目のセルの次のステップの状態は、その両隣と自分自身、すなわち、$i-1$, $i$、$i+1$番目の3つのセルの状態によって決める。 自分と両隣の状態は、全部で $2^3$ 通りあるから、8つのパターンのそれぞれに、次の状態として0か1を割り当てることができる。 つまり、8つのそれぞれに2通りの選択肢が可能であるから、全体では$2^8$通りのルールが可能となるわけだ。
そこで、この8ビットのパターンを0から255までの数値と見なして、セル・オートマトンの状態遷移ルールを、その数値で表すのが一般的である。 例えば、以下はルール90の例である。
反対に、ルール番号 $R$ が与えられたとき、自分と両隣のパターンが $(b_2, b_1, b_0)$であったとすると、 $R$を二進数で表現した際の下の桁から$4 b_2 + 2 b_1 + b_0$ビット目が、次のステップの状態となることがわかる。
シミュレーション
以上のように、セル・オートマトンは他のモデル(例えば偏微分方程式モデル)等に比べれば遥かに単純に見える一方で、 それがどのように振る舞うのかを直感することは、なかなか困難である。 そこで、実際にどんな様子になるのかシミュレーションしてみよう。 状態が変化する様子を観察するために、Pygletというライブラリを使い、アニメーションによって可視化することにする。 以下はそのコードの例である。
状態をNumPyの一次元配列(サイズは$N$)stateに記憶しておいて、関数update_state()で更新している。
$k$番目のセルとその両隣の状態はstate[(k-1)%N]*4 + state[k]*2 + state[(k+1)%N]によって数値化し、
ルール番号RULEの当該のビットの値を調べることで、次の状態を選択するようにしている。
$k$番目のセルの両隣の番号を(k-1)%Nあるいは(k+1)%Nで指定することで、周期的な境界条件としている。
ここで、Pythonでは負の数の剰余 -1%N は N-1 を与えることに注意。
初期条件は、関数init_state()で乱数を用いて設定している。
Pygletを用いて、$N \times M$の矩形を敷き詰めて、状態遷移に応じて色を変えつつ、時間の経過と共に画面がスクロールするようにプログラムされている。
実行には、Pyglet(バージョン2以上)がインストールされた環境が必要。
pip install pyglet等のコマンドを使ってインストールできる。
import numpy as np
import random
import math
import pyglet
from pyglet.gl import *
N = 256
M = 256
RULE = 110
SCALE=4
state = np.zeros(shape=(N,), dtype='int32')
state2 = np.zeros(shape=(N,), dtype='int32')
nstep = 0
def update_state():
global nstep
for k in range(N):
i = state[(k-1)%N] * 4 + state[k] * 2 + state[(k+1)%N]
if (1<<i) & RULE:
state2[k] = 1
else:
state2[k] = 0
state[:] = state2[:]
nstep += 1
def init_state():
state[:] = np.random.choice([0,1], size=N, p=(0.95,0.05))[:]
config = pyglet.gl.Config(double_buffer=True)
window = pyglet.window.Window(N*SCALE,M*SCALE,config=config,resizable=False)
window.set_caption('1D Cellular Automaton')
batch = pyglet.graphics.Batch()
tiles = np.empty(shape=(N,M),dtype='object')
def init_tiling():
for i in range(N):
for j in range(M):
shape = pyglet.shapes.Rectangle(x=i*SCALE, y=j*SCALE, width=SCALE, height=SCALE, color=(0, 0, 0), batch=batch)
tiles[i,j] = shape
for i in range(N):
if state[i]==0:
tiles[i,0].color = (10,10,70)
elif state[i]==1:
tiles[i,0].color = (200,100,90)
else: # owtherwise something went wrong...
tiles[i,0].color = (255,255,0)
def update_tiling():
for j in range(M-1,0,-1):
t1 = tiles[:,j-1]
t0 = tiles[:,j]
for i in range(N):
t0[i].color = t1[i].color
for i in range(N):
if state[i]==0:
tiles[i,0].color = (10,10,70)
else:
tiles[i,0].color = (200,100,90)
@window.event
def on_draw():
window.clear()
batch.draw()
str = 'T={0:4d}'.format(nstep)
label_time = pyglet.text.Label(str,font_name='Helvetica', color=(255,255,255,255), font_size=12, x=10, y=12)
label_time.draw()
def update(deltat):
update_state()
update_tiling()
init_state()
init_tiling()
pyglet.clock.schedule_interval(update, 1/120.0)
pyglet.app.run()
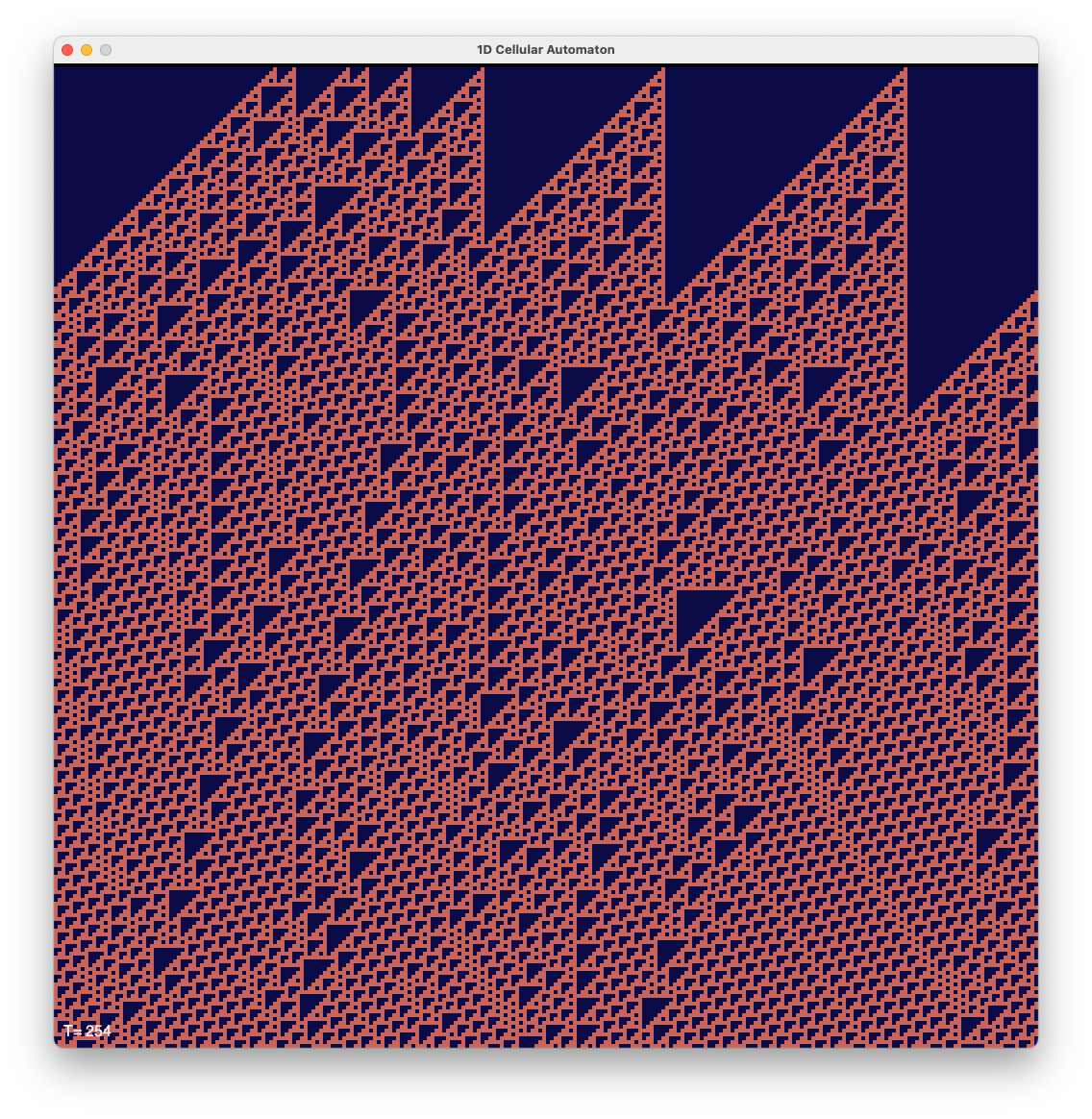
以下はこのコードを使ってルール番号110のシミュレーションを行った例(スクリーンショット)である。 時間ステップは、画面の上から下側に進行しており、状態1を赤茶色、状態0を暗い青色で表示している。
 練習:コードの最適化と観察
練習:コードの最適化と観察
上で示したサンプルコードは、状態遷移に伴って全ての四角形の色を二重ループで更新するなど、非効率なところが多い(とても遅い)。 そこで、コードを改良(改造)して、より長期的な挙動も観察できるように工夫してみなさい。
更に、改良したコードを使って、変数RULEで指定されているルール番号を0から255の範囲で変えてみて、出現するパターンの違いを調べ分類してみなさい。
 ヒント
ヒント
参考として、NumPyやPygletの機能を使って効率化を図ってみたサンプルコード 1d-ca-faster-version.pyを用意しておいた。
2次元のセル・オートマトン
コンウェイのライフゲーム
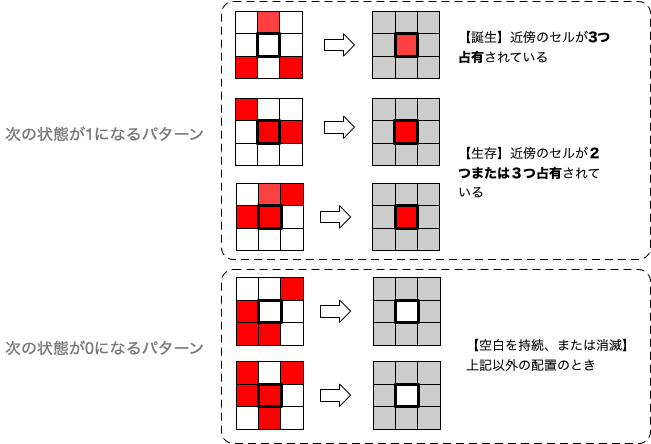
空間を碁盤の目のようなセルに分割して、上下左右と斜め方向を含む8つの近傍の状態に応じて、0か1かのどちらかの状態に遷移するルールを考える。 ここでは、生物の増殖過程を想定しながら、0はその場所が空の状態、1はそこに生物が生存している状況を表すものとし、
- 近傍の3つのセルが1の状態のとき、0だったセルは1に遷移する(「子供」が生まれる)
- 近傍の2つ、または3つのセルが1の状態のとき、1のセルは1のままとする(生存)
- それ以外の場合は、セルの状態は0に変化する(過疎または過密による死滅)
というルールを考える。
これはライフゲーム(Game of Life)として知られている数理モデルである。
以下は、Pygletを使って状態遷移の様子をアニメーションで表示するコードの例である。 近傍の1のセルの数をNumPyのrollと総和を使って求めたり、状態に応じた条件分岐をNumPyのwhere機能を使うなど、 できるだけ多重ループを使わないよう工夫している。
実行にはPyglet(バージョン2以上)がインストールされたPCが必要。
import numpy as np
import random
import math
import pyglet
from pyglet.gl import *
N = 128
SCALE=8
state = np.zeros(shape=(N,N), dtype='int32')
state_prev = np.zeros(shape=(N,N), dtype='int32')
nstep = 0
def compute_neighbors_sum(array):
rolled_up = np.roll(array, -1, axis=0)
rolled_down = np.roll(array, 1, axis=0)
rolled_left = np.roll(array, -1, axis=1)
rolled_right = np.roll(array, 1, axis=1)
rolled_up_left = np.roll(rolled_up, -1, axis=1)
rolled_up_right = np.roll(rolled_up, 1, axis=1)
rolled_down_left = np.roll(rolled_down, -1, axis=1)
rolled_down_right = np.roll(rolled_down, 1, axis=1)
neighbors_sum = (
rolled_up + rolled_down + rolled_left + rolled_right +
rolled_up_left + rolled_up_right + rolled_down_left + rolled_down_right
)
return neighbors_sum
def update_state():
global nstep
neighbor_sum = compute_neighbors_sum(state)
s1 = np.zeros(shape=(N,N), dtype='int32')
cond1 = (state == 0) & (neighbor_sum == 3)
s1 = np.where(cond1, 1, s1)
s2 = np.zeros(shape=(N,N), dtype='int32')
cond2 = (state == 1) & ((neighbor_sum == 2) | (neighbor_sum == 3))
s2 = np.where(cond2, 1, s2)
state_prev[:,:] = state[:,:]
state[:,:] = s1[:,:] + s2[:,:]
nstep += 1
def init_state():
state[:,:] = np.random.choice([0,1], size=(N,N), p=(0.5,0.5))[:]
config = pyglet.gl.Config(double_buffer=True)
window = pyglet.window.Window(N*SCALE,N*SCALE,config=config,resizable=False)
window.set_caption('Life Game')
batch = pyglet.graphics.Batch()
tiles = np.empty(shape=(N,N),dtype='object')
def init_tiling():
for i in range(N):
for j in range(N):
shape = pyglet.shapes.Rectangle(x=i*SCALE, y=j*SCALE, width=SCALE, height=SCALE, color=(0, 0, 0), batch=batch)
tiles[i,j] = shape
for i in range(N):
for j in range(N):
if state[i,j]==0:
tiles[i,j].color = (10,10,70)
elif state[i,j]==1:
tiles[i,j].color = (200,100,90)
else: # owtherwise something went wrong...
tiles[i,j].color = (255,255,0)
def update_tiling():
diff = (state != state_prev)
indices = np.argwhere(diff)
for i,j in indices:
if state[i,j]==0:
tiles[i,j].color = (10,10,70)
else:
tiles[i,j].color = (200,100,90)
@window.event
def on_draw():
window.clear()
batch.draw()
str = 'T={0:4d}'.format(nstep)
label_time = pyglet.text.Label(str,font_name='Helvetica', color=(255,255,255,255), font_size=12, x=10, y=12)
label_time.draw()
def update(deltat):
update_state()
update_tiling()
init_state()
init_tiling()
pyglet.clock.schedule_interval(update, 1/100.0)
pyglet.app.run()
ライフゲームのコードの実行例。 PC上で動作する様子を実時間でキャプチャしたもの。
ラングトンのループ
セル・オートマトンは、生物の特徴である自己複製能力を備えた機械をどのように記述したり設計したりできるかを研究する中で案出された経緯がある。 人工生命(Artificial Life)の研究の中で、C. ラングトンは二次元セル・オートマトンを使って、矩形のようなパターンが自己複製しながら増殖する実例を示している。 そのルールは、ライフゲームと比べるとかなり複雑で、表の形で記述されている。
下記は、それをシミュレーションするコードの例である。
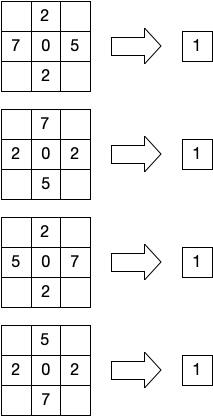
リスト langton_rulesの各要素は遷移ルールを表しており、例えば
(0,2,5,2,7,1)は、
のような遷移ルールを表している。回転対称なルールも含むため、この例のように、要素1つあたり4つのルールが対応する。 列挙されている遷移パターンと照合することで、自分自身と上下左右の5つのセルの状態に応じて自分自身の状態が更新される。
実行にはPyglet(バージョン2以上)がインストールされたPCが必要。
import numpy as np
langton_rules = [
(0,0,0,0,0,0),(0,2,5,2,7,1),(1,1,3,2,2,1),(2,0,2,4,2,2),(3,0,1,0,2,1),
(0,0,0,0,1,2),(1,0,0,0,1,1),(1,2,2,2,4,4),(2,0,2,4,5,2),(3,0,1,2,2,0),
(0,0,0,0,2,0),(1,0,0,0,6,1),(1,2,2,2,7,7),(2,0,2,5,2,0),(3,0,2,5,1,1),
(0,0,0,0,3,0),(1,0,0,0,7,7),(1,2,2,4,3,4),(2,0,2,5,5,2),(4,0,1,1,2,0),
(0,0,0,0,5,0),(1,0,0,1,1,1),(1,2,2,5,4,7),(2,0,2,6,2,2),(4,0,1,2,2,0),
(0,0,0,0,6,3),(1,0,0,1,2,1),(1,2,3,2,4,4),(2,0,2,7,2,2),(4,0,1,2,5,0),
(0,0,0,0,7,1),(1,0,0,2,1,1),(1,2,3,2,7,7),(2,0,3,1,2,2),(4,0,2,1,2,0),
(0,0,0,1,1,2),(1,0,0,2,4,4),(1,2,4,2,5,5),(2,0,3,2,1,6),(4,0,2,2,2,1),
(0,0,0,1,2,2),(1,0,0,2,7,7),(1,2,4,2,6,7),(2,0,3,2,2,6),(4,0,2,3,2,6),
(0,0,0,1,3,2),(1,0,0,5,1,1),(1,2,5,2,7,5),(2,0,3,4,2,2),(4,0,2,5,2,0),
(0,0,0,2,1,2),(1,0,1,0,1,1),(2,0,0,0,1,2),(2,0,4,2,2,2),(4,0,3,2,2,1),
(0,0,0,2,2,0),(1,0,1,1,1,1),(2,0,0,0,2,2),(2,0,5,1,2,2),(5,0,0,0,2,2),
(0,0,0,2,3,0),(1,0,1,2,4,4),(2,0,0,0,4,2),(2,0,5,2,1,2),(5,0,0,2,1,5),
(0,0,0,2,6,2),(1,0,1,2,7,7),(2,0,0,0,7,1),(2,0,5,2,2,2),(5,0,0,2,2,5),
(0,0,0,2,7,2),(1,0,2,0,2,6),(2,0,0,1,2,2),(2,0,5,5,2,1),(5,0,0,2,3,2),
(0,0,0,3,2,0),(1,0,2,1,2,1),(2,0,0,1,5,2),(2,0,5,7,2,5),(5,0,0,2,7,2),
(0,0,0,5,2,5),(1,0,2,2,1,1),(2,0,0,2,1,2),(2,0,6,2,2,2),(5,0,0,5,2,0),
(0,0,0,6,2,2),(1,0,2,2,4,4),(2,0,0,2,2,2),(2,0,6,7,2,2),(5,0,2,0,2,2),
(0,0,0,7,2,2),(1,0,2,2,6,3),(2,0,0,2,3,2),(2,0,7,1,2,2),(5,0,2,1,2,2),
(0,0,1,0,2,2),(1,0,2,2,7,7),(2,0,0,2,4,2),(2,0,7,2,2,2),(5,0,2,1,5,2),
(0,0,1,1,2,0),(1,0,2,3,2,7),(2,0,0,2,5,0),(2,0,7,4,2,2),(5,0,2,2,2,0),
(0,0,2,0,2,0),(1,0,2,4,2,4),(2,0,0,2,6,2),(2,0,7,7,2,2),(5,0,2,2,4,4),
(0,0,2,0,3,0),(1,0,2,6,2,6),(2,0,0,2,7,2),(2,1,1,2,2,2),(5,0,2,7,2,2),
(0,0,2,0,5,0),(1,0,2,6,4,4),(2,0,0,3,2,6),(2,1,1,2,6,1),(5,1,2,1,2,2),
(0,0,2,1,2,5),(1,0,2,6,7,7),(2,0,0,4,2,3),(2,1,2,2,2,2),(5,1,2,2,2,0),
(0,0,2,2,2,0),(1,0,2,7,1,0),(2,0,0,5,1,7),(2,1,2,2,4,2),(5,1,2,4,2,2),
(0,0,2,3,2,2),(1,0,2,7,2,7),(2,0,0,5,2,2),(2,1,2,2,6,2),(5,1,2,7,2,2),
(0,0,5,2,2,2),(1,0,5,4,2,7),(2,0,0,5,7,5),(2,1,2,2,7,2),(6,0,0,0,1,1),
(0,1,2,3,2,1),(1,1,1,1,2,1),(2,0,0,7,2,2),(2,1,4,2,2,2),(6,0,0,0,2,1),
(0,1,2,4,2,1),(1,1,1,2,2,1),(2,0,1,0,2,2),(2,1,5,2,2,2),(6,0,2,1,2,0),
(0,1,2,5,2,5),(1,1,1,2,4,4),(2,0,1,1,2,2),(2,1,6,2,2,2),(6,1,2,1,2,5),
(0,1,2,6,2,1),(1,1,1,2,5,1),(2,0,1,2,2,2),(2,1,7,2,2,2),(6,1,2,1,3,1),
(0,1,2,7,2,1),(1,1,1,2,6,1),(2,0,1,4,2,2),(2,2,2,2,7,2),(6,1,2,2,2,5),
(0,1,2,7,5,1),(1,1,1,2,7,7),(2,0,1,7,2,2),(2,2,2,4,4,2),(7,0,0,0,7,7),
(0,1,4,2,2,1),(1,1,1,5,2,2),(2,0,2,0,2,2),(2,2,2,4,6,2),(7,0,1,1,2,0),
(0,1,4,3,2,1),(1,1,2,1,2,1),(2,0,2,0,3,2),(2,2,2,7,6,2),(7,0,1,2,2,0),
(0,1,4,4,2,1),(1,1,2,2,2,1),(2,0,2,0,5,2),(2,2,2,7,7,2),(7,0,1,2,5,0),
(0,1,4,7,2,1),(1,1,2,2,4,4),(2,0,2,0,7,3),(3,0,0,0,1,3),(7,0,2,1,2,0),
(0,1,6,2,5,1),(1,1,2,2,5,1),(2,0,2,1,2,2),(3,0,0,0,2,2),(7,0,2,2,2,1),
(0,1,7,2,2,1),(1,1,2,2,7,7),(2,0,2,1,5,2),(3,0,0,0,4,1),(7,0,2,2,5,1),
(0,1,7,2,5,5),(1,1,2,3,2,1),(2,0,2,2,1,2),(3,0,0,0,7,6),(7,0,2,3,2,1),
(0,1,7,5,2,1),(1,1,2,4,2,4),(2,0,2,2,2,2),(3,0,0,1,2,3),(7,0,2,5,2,5),
(0,1,7,6,2,1),(1,1,2,6,2,1),(2,0,2,2,7,2),(3,0,0,4,2,1),(7,0,2,7,2,0),
(0,1,7,7,2,1),(1,1,2,7,2,7),(2,0,2,3,2,1),(3,0,0,6,2,2)
]
rule_tab = np.zeros(shape=(8,8,8,8,8),dtype='uint8')
for c,t,r,b,ell,s in langton_rules:
rule_tab[c,t,r,b,ell] = s
rule_tab[c,ell,t,r,b] = s
rule_tab[c,b,ell,t,r] = s
rule_tab[c,r,b,ell,t] = s
#####
import random
import math
import pyglet
from pyglet.gl import *
N = 128
SCALE=8
state = np.zeros(shape=(N,N), dtype='uint8')
state2 = np.zeros(shape=(N,N), dtype='uint8')
state_prev = np.zeros(shape=(N,N), dtype='uint8')
nstep = 0
def update_state():
global nstep
c = state
ell = np.roll(state, -1, axis=0)
t = np.roll(state, -1, axis=1)
r = np.roll(state, 1, axis=0)
b = np.roll(state, 1, axis=1)
state2 = rule_tab[c, t, r, b, ell]
state_prev[:,:] = state[:,:]
state[:,:] = state2[:,:]
nstep += 1
def init_state():
state0 = np.array([
[0,2,2,2,2,2,2,2,2,0,0,0,0,0,0],
[2,1,7,0,1,4,0,1,4,2,0,0,0,0,0],
[2,0,2,2,2,2,2,2,0,2,0,0,0,0,0],
[2,7,2,0,0,0,0,2,1,2,0,0,0,0,0],
[2,1,2,0,0,0,0,2,1,2,0,0,0,0,0],
[2,0,2,0,0,0,0,2,1,2,0,0,0,0,0],
[2,7,2,0,0,0,0,2,1,2,0,0,0,0,0],
[2,1,2,2,2,2,2,2,1,2,2,2,2,2,0],
[2,0,7,1,0,7,1,0,7,1,1,1,1,1,2],
[0,2,2,2,2,2,2,2,2,2,2,2,2,2,0]
],dtype='uint8').T
state[N//2-8:N//2+7, N//2-5:N//2+5] = state0[:,:]
config = pyglet.gl.Config(double_buffer=True)
window = pyglet.window.Window(N*SCALE,N*SCALE,config=config,resizable=False)
window.set_caption('Langton\'s loops')
batch = pyglet.graphics.Batch()
tiles = np.empty(shape=(N,N),dtype='object')
def coloring(s):
if s==0:
return (10,10,70)
elif s==1:
return (200,100,90)
elif s==2:
return (200,100,120)
elif s==3:
return (100,100,90)
elif s==4:
return (100,100,200)
elif s==5:
return (70,80,200)
elif s==6:
return (10,200,90)
elif s==7:
return (30,200,200)
def init_tiling():
for i in range(N):
for j in range(N):
shape = pyglet.shapes.Rectangle(x=i*SCALE, y=j*SCALE, width=SCALE, height=SCALE, color=(0, 0, 0), batch=batch)
tiles[i,j] = shape
for i in range(N):
for j in range(N):
tiles[i,j].color = coloring(state[i,j])
def update_tiling():
diff = (state != state_prev)
indices = np.argwhere(diff)
for i,j in indices:
tiles[i,j].color = coloring(state[i,j])
@window.event
def on_draw():
window.clear()
batch.draw()
str = 'T={0:4d}'.format(nstep)
label_time = pyglet.text.Label(str,font_name='Helvetica', color=(255,255,255,255), font_size=12, x=10, y=12)
label_time.draw()
def update(deltat):
update_state()
update_tiling()
init_state()
init_tiling()
pyglet.clock.schedule(update)
pyglet.app.run()
「ラングトンのループ」のコードの実行例。 PC上で動作する様子を実時間でキャプチャしたもの。