Pythonプログラミング（ステップ７・平均値の検定とt分布）

このページでは、t検定を行う際に必要となるt統計量とその分布関数について考える。

平均値の検定

平均 $\mu$ と分散 $\sigma^2$ は不明であるものの、正規分布に従うことはわかっている母集団 X から、$n$個のデータを取得したとしよう。 $i$番目のデータを $X_i$ と表記することにする。 このサンプルから、母平均がある値（例えば0）であると見なしてよいかどうか、統計的に吟味したいとしよう。

言うまでもなく、母平均はサンプルの平均 $$ \bar{X} = \frac{1}{n} \sum_{i=1}^n X_i $$ によって推定できるが、$n$が十分に大きくない限り、$\bar{X}$の値は無視できない程度の確率的な変動を伴うはずだ。 そして、その変動は正規分布 $$ \bar{X} \sim N(\mu, \sigma^2/n) $$ に従う。しかしながら、母平均 $\mu$ と母分散 $\sigma^2$ は不知である。

このような設定の下で、得られたサンプル平均がどれくらい予想される値として理解可能なのかを吟味する（平均値の検定を行う）には、どのようにすればよいだろうか。

t統計量

$Y$を正規分布に従う確率変数とする。 観測によってその不偏分散が$U^2$と推定されているとき、 $$ T = \frac{Y - m}{U} \tag{1} $$ で定義される量を t統計量と呼ぶ。 このt統計量は、$U$で規格化されているため、母分散の大小には依らず、$Y$の$m$からの系統的な「ずれ」に対する統一的な指標となることが期待できる。

さて、正規分布に従うXから、$n$回の観測によって $X_1, X_2, \cdots, X_n$ のサンプルが得られたとすると、 Xの不偏分散は $$ {U_X}^2 = \frac{1}{n-1} \sum_{i=1}^n \left( X_i - \bar{X} \right)^2 $$ で与えられる。

ここで X の標本平均 $$ \bar{X} = \frac{1}{n} \sum_{i=1}^n X_i $$ を確率変数と見なせば、標本平均の不変分散 $U^2$ は Xの不偏分散 $U^2_X$を使って $$ U^2 = \left. {U_X}^2 \middle/ n \right. $$ となる。

そこで、(1)式のt統計量の定義で $Y=\bar{X}$ とおけば、平均についてのt統計量 $$ T = \frac{Y - m}{U} = \frac{\bar{X} - m}{U_X \Big/ \sqrt{n}} \tag{2} $$ を構成できる。

(1)式では $\bar{X}$ の分散の大小をちょうど相殺するようにこれを$U_X/\sqrt{n}$で割った格好になっている。 ここで、分子の$\bar{X}$も、分母の$U_X$も、共にサンプル毎に確率的に変動するので、全体として$T$は正規分布とはならない （ただし$n$が十分大きければ、不偏分散は$\sigma^2/n$に近づくから、$t$は平均0分散1の正規分布に漸近する）。

このt統計量を使うと、比較的サンプル数が少ない場合でも、『母集団の平均が $m$ である』という帰無仮説を設定して、 分散の大小には影響されることなく検定することができる。

このt統計量は t分布と呼ばれる分布関数に従うことが知られている： $$ f(t) = \frac{\Gamma((\nu+1)/2)}{\sqrt{\nu\pi}\,\Gamma(\nu/2)} \left( 1 + t^2/\nu \right)^{-(\nu+1)/2} \tag{3} $$ ここで、$\nu = n-1$は分布の自由度と呼ばれる。$\Gamma( )$はガンマ関数である。

自由度1のt分布

デルタ関数を使ってt分布関数を表現する

では、t統計量はどのような確率分布をするのか、その様子を見るために、最も自由度の小さな場合（$\nu=1$）について考えよう。 平均は0、分散$\sigma^2$のガウス分布に従う独立な確率変数 $X$ と $Y$ から（ここでの$Y$は前節の説明とは関係ない）、(2)式に従ってt統計量を「合成」すると $$ T = \frac{(X+Y)\big/2}{\sqrt{\left(X-\frac{(X+Y)}{2}\right)^2 + \left(Y-\frac{(X+Y)}{2}\right)^2}\big/\sqrt{2}} $$ となる。 この$T$が従う分布関数 $f(t)$ を具体的に調べてみよう。

デルタ関数を使うと、$f(t)$は $$ f(t) = \frac{1}{\left(\sqrt{2\pi}\sigma\right)^2} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \delta\left(t - \frac{(x+y)\big/2}{\sqrt{\left(x-\frac{(x+y)}{2}\right)^2 + \left(y-\frac{(x+y)}{2}\right)^2}\big/\sqrt{2}}\right) \exp\left[ -\frac{x^2 + y^2}{2 \sigma^2} \right] dx dy $$ と表現することができるので、この式から出発して考えてみる。

積分を極座標に変換し、動径方向と角度方向の積分に分ける

このままでは見通しが悪いので、積分を極座標 $$ x = r \cos\theta, \; y=r \sin\theta $$ に変数変換すると $$ f(t) = \frac{1}{\left(\sqrt{2\pi}\sigma\right)^2} \int_{0}^{2\pi} \int_{0}^{+\infty} \delta\left(t - \frac{\cos\theta+\sin\theta}{|\cos\theta - \sin\theta|}\right) \exp\left[ -\frac{r^2}{2 \sigma^2} \right] \, r \, dr \, d\theta $$ $$ = \frac{1}{2\pi\sigma^2} \int_{0}^{+\infty} r \exp\left[ -\frac{r^2}{2 \sigma^2} \right] dr \int_{0}^{2\pi} \delta\left(t - \frac{\cos\theta+\sin\theta}{|\cos\theta - \sin\theta|}\right) d \theta $$ となる。デルタ関数の中の$r$は分子と分母でキャンセルして消えることに注意。ここで、$r$についての積分は $$ \int_{0}^{+\infty} r \exp\left[ -\frac{r^2}{2 \sigma^2} \right] dr = \sigma^2 $$ となる。

$\theta$についての積分は、絶対値の中の符号に気をつけながら書き下すと $$ \begin{eqnarray} \int_{0}^{2\pi} \delta\left(t - \frac{\cos\theta+\sin\theta}{|\cos\theta - \sin\theta|}\right) d \theta \\ = \int_{0}^{\pi/4} \delta\left(t - \frac{\cos\theta+\sin\theta}{\cos\theta - \sin\theta}\right) d \theta \\ + \int_{\pi/4}^{3\pi/4} \delta\left(t - \frac{\cos\theta+\sin\theta}{\sin\theta-\cos\theta}\right) d \theta \\ + \int_{3\pi/4}^{2 \pi} \delta\left(t - \frac{\cos\theta+\sin\theta}{\cos\theta - \sin\theta}\right) d \theta \end{eqnarray} $$ となる。ここで、変数変換 $$ s = t - \frac{\cos\theta+\sin\theta}{|\cos\theta - \sin\theta|} $$ を施すと $$ \frac{d\theta}{ds} = \mp \frac{1}{2} \frac{(1-\tan\theta)^2}{1 + \tan^2\theta} $$ $$ \tan\theta(t,s) = \frac{\mp 1 + (t -s)}{\pm 1 + (t -s)} $$ であるから（複号同順）、デルタ関数の性質、および$\frac{(1-\tan\theta(t,0))^2}{1 + \tan^2\theta(t,0)} = \frac{2}{1+t^2}$を使って $$ \begin{eqnarray} \int_{0}^{2\pi} \delta\left(t - \frac{\cos\theta+\sin\theta}{|\cos\theta - \sin\theta|}\right) d \theta \\ = - \frac{1}{2} \int_{t - 1}^{t - \infty} \delta(s) \frac{(1-\tan\theta(t,s))^2}{1 + \tan^2\theta(t,s)} d s \\ + \frac{1}{2} \int_{t - \infty}^{t + \infty} \delta(s) \frac{(1-\tan\theta(t,s))^2}{1 + \tan^2\theta(t,s)} d s \\ - \frac{1}{2} \int_{t + \infty}^{t - 1} \delta(s) \frac{(1-\tan\theta(t,s))^2}{1 + \tan^2\theta(t,s)} d s \end{eqnarray} $$ $$ = \frac{2}{1+t^2} $$ を得る（この部分は実質的に積分計算は不要）。 計算の過程で、ある$t$に対して、$s$の積分区間が0をよぎるのは、上記の3つ項のうちの2つであること、 そして、全体にマイナス符号が付いている積分は、積分範囲が「大きいほうから小さいほう」の向きである点に注意。

結果をまとめて1自由度のt分布関数を得る

以上をまとめると、２つの確率変数に対するt分布関数（自由度1）は $$ f(t) = \frac{1}{\pi(1+t^2)} $$ であることがわかった。 このように、自由度が小さい場合、t分布と正規分布はかなり異なることに注意が必要である。

t統計量の分布は母分散に依らない

変数が$n$個（自由度が$n-1$)の場合でも同様に、極座標で積分すると（動径成分を$r$、角度成分を$\Theta$、角度変数のヤコビ行列式を$J(\Theta)$と表記すると） $$ f(t) = \frac{1}{\left(\sqrt{2\pi}\sigma\right)^n} \int_{0}^{+\infty} r^{n-1} \exp\left[ -\frac{r^2}{2 \sigma^2} \right] dr \int \delta\left(t - G(\Theta))\right) J(\Theta) d\Theta $$ のように$r$と$\Theta$の積分を分けることができて、 $$ \int_{0}^{+\infty} r^{n-1} \exp\left[ -\frac{r^2}{2 \sigma^2} \right] dr = 2^{\frac{n}{2}-1} \Gamma(n/2) \sigma^n $$ であることを使うと $$ f(t) = \frac{\Gamma(n/2)}{2 \sqrt{\pi^n}} \int \delta\left(t - G(\Theta))\right) J(\Theta) d\Theta $$ となって、分布関数は$\sigma$に依存しないことがわかる （t統計量は標本平均を不偏分散の平方根で規格化した量なので、これは当然である）。

標本平均と分散を確率変数と見なして計算する

このように、ガウス分布するランダムな変数から出発してt分布関数を求めるのは結構な骨が折れるので、 通常は、標本平均$\bar{X}$と不偏分散$U^2$をそれぞれ独立なランダムな変数と考えて計算を行う。例えば上記の自由度1の場合は、

$$ \begin{eqnarray} f(t) & = & \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} \delta\left(t - \frac{w}{u\big/\sqrt{2}}\right) \delta\left(u - \sqrt{\left(x-w\right)^2 + \left(y-w\right)^2} \right) \delta\left(w - (x+y)\big/2 \right) \frac{e^{-\frac{x^2 + y^2}{2 \sigma^2}} }{\left(\sqrt{2\pi}\sigma\right)^2} dx dy \\ & = & \int_{-\infty}^{+\infty} dw \int_{0}^{+\infty} du \; \delta\left(t - \frac{w}{u\big/\sqrt{2}}\right) g(u) h(w) \end{eqnarray} $$ のように予め式を変形しておけば、標本平均の分布関数$h(w)$と不偏分散の平方根の分布関数$g(u)$から計算を出発することができる。 詳しくは専門書にあたること。

平均値のt検定

30cmのものさしを作っている工場があったとする。 製品の中からランダムに$5$個のサンプルを抽出し、実際の長さを検査してみたとしよう。 ここで、帰無仮説として「製品（ものさし）の平均の長さは30cmである」を設け、 これを検定してみよう。

製品の誤差が正規分布すると考えるのは自然であるから、t統計量を使った検定を行うための前提を満たしている。

サンプルから得た長さ$\ell_i$[cm]から、標本平均 $$ w = \frac{1}{5} (\ell_1 + \ell_2 + \ell_3 + \ell_4 + \ell_5) $$ と、不偏分散 $$ u^2 = \frac{1}{4} \left[ (\ell_1 - w)^2 + (\ell_2 - w)^2 + (\ell_3 - w)^2 + (\ell_4 - w)^2 + (\ell_5 - w)^2 \right] $$ が得られるから、それらを用いて t統計量 $$ t = \frac{w - 30}{u / \sqrt{5}} $$ を求める。得られた $t$ が生じるであろう確率が有意水準よりも小さければ、帰無仮説は棄却される（製品の平均長が30cmである可能性は確率的に小さい）。

自由度$\nu$のt分布関数を$f_{\nu}(t)$とすると、両側検定の場合、 $\pm |t|$よりも分布の端を占める割合 $$ F_{\nu}(t) =\int_{-\infty}^{-|t|} f_\nu(s) ds + \int_{|t|}^{\infty} f_\nu(s) ds = 2 \int_{|t|}^{\infty} f_\nu(s) ds $$ を求め、有意水準(例えば0.05)と比較すればよい（t分布関数は中心対称なので、片側分だけ計算して２倍すればよい）。

　練習：ものさしチェッカー

ものさしの実測値を5件入力して、「製品の平均の長さが30cmである」かどうかを有意水準5%で判定するコードを作成しなさい。

　ヒント

コードの先頭部分に

import math

def tdist(t,nu):
    return math.gamma((nu+1)/2)/(math.sqrt(nu*math.pi)*math.gamma(nu/2)) * (1+t**2/nu)**(-(nu+1)/2)

と記述することで、自由度$\nu$のt分布関数をtdist(t,nu)によって呼び出せるようになる。

積分の計算には台形法を用いよ。 DE法（半無限区間）を使うと、さらに精度を高めることができるはずである。

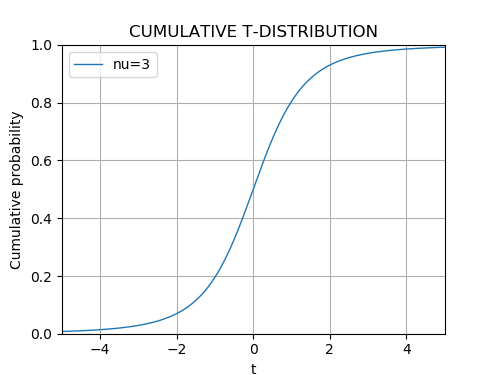
あるいは、SciPyライブラリのscipy.stats.tを使えば、t分布の累積分布を簡単に求めることができる。 以下は、t分布の累積密度関数をプロットするコードの例である：

# coding: utf-8

import math
import numpy as np
from scipy.stats import t
import matplotlib.pyplot as plt

nu = 3

xaxis = np.arange(-5, 5, 0.01)
tcdf = t.cdf(xaxis,nu)

plt.plot(xaxis,tcdf,'-', linewidth=1.0, label="nu="+str(nu))

plt.title("CUMULATIVE T-DISTRIBUTION")
plt.xlim(-5,5)
plt.ylim(0,1)
plt.legend()
plt.xlabel('x')
plt.ylabel('Cumulative probability')
plt.grid(True)
plt.show()

平均値の信頼区間

正規分布に従う母集団 からの$n$個のサンプル $X_1, X_2, \cdots, X_n$ が得られているとき、 母平均は「どの範囲」にあると考えられるだろうか。 大数の法則から、標本平均 $$ \bar{X} = \frac{1}{n} \sum_i X_i $$ は $n \to \infty$ で 母平均 $\mu$ に漸近することが保証されているものの、 $n$がそれほど大きくなければ $\bar{X}$ は $\mu$ の周りで確率的に揺らぐ。

その様子を推定するには、 t統計量 $$ T = \frac{\bar{X} - m}{U \Big/\sqrt{n}} $$ を考え、$m$ の範囲を色々と変えてみて、確率密度（t分布関数）の山の中央付近をとればよさそうである。 t検定の帰無仮説を設定する際の$m$の値を沢山試してみて、帰無仮説が棄却されるような$m$の範囲だけ除くわけである。

平均値の例えば95%信頼区間を見積もるには、t分布密度の両端の面積が 0.025 に相当する部分を除いた、中央の範囲を取ればよい。 その境い目となる $T$ の値を、それぞれ $-T^*$, $+T^*$ とすれば、 $$ -T^* \le \frac{\bar{X} - m}{U \Big/\sqrt{n}} \le +T^* $$ であり、これから $m$ の信頼区間は $$ \bar{X} - T^* U/\sqrt{n} \le m \le \bar{X} + T^* U/\sqrt{n} $$ で与えられる。

データを与えて、その平均値の95%の信頼区間を出力するPythonコードの例を以下に示す。 t分布の計算にはSciPyライブラリを用いている。 確率からt値を逆算するために ppf()関数が用意されている。

# coding: utf-8

import math
import numpy as np
from scipy.stats import t
import matplotlib.pyplot as plt

X=[29.978, 29.933, 29.9245, 30.0944, 30.0981]
n = len(X)
nu = n-1

x = np.array(X)
s = np.mean(x)
u2 = np.var(x,ddof=1)
u = np.sqrt(u2)

t_lower = t.ppf(0.025, nu)
t_upper = t.ppf(1-0.025, nu)

m_lower = - t_upper * u/n + s
m_upper= - t_lower * u/n + s

print(m_lower, m_upper)

xaxis_low = np.arange(-5, t_lower, 0.01)
xaxis_mid = np.arange(t_lower, t_upper, 0.01)
xaxis_upper = np.arange(t_upper, 5, 0.01)
tdist_low = t.pdf(xaxis_low,nu)
tdist_mid = t.pdf(xaxis_mid,nu)
tdist_upper = t.pdf(xaxis_upper,nu)

fig = plt.figure()
ax = fig.add_subplot(111)
ax.grid()
ax.fill_between(xaxis_low,tdist_low,'-', color='red')
ax.plot(xaxis_mid,tdist_mid,'-', color='blue', linewidth=1.0, label="nu="+str(nu))
ax.fill_between(xaxis_upper,tdist_upper,'-', color='red', linewidth=1.0)
ax.set_title("T-DISTRIBUTION")
ax.set_xlim(-5,5)
ax.set_yticks([0, 0.1, 0.2, 0.3, 0.4])
ax.set_yticklabels(["0", "0.1", "0.2", "0.3", "0.4"])
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('p(x)')
plt.show()