Pythonプログラミング（ステップ７・確率密度関数とその計算）

このページでは、確率密度関数の計算について復習する。

確率密度関数

ランダムな変量（確率変数）$X$を考える。 計測のたびに、連続値（例えば電圧や時間等々）が確率的に変動する例は枚挙にいとまがないが、連続的な量の場合には、 「電圧がちょうど1.0000Vになる可能性」を議論するのは不適切で、 「電圧が 0.9Vから1.1Vの間にある可能性」のように問題設定を行う必要がある。 そのような状況に対応すべく、 $X$ が $x_1$ から $x_2$ $(x_1 \lt x_2)$ の間にある確率を、$X$の確率密度関数 $f(x)$ を使って $$ P[x_1 \lt X \lt x_2] = \int_{x_1}^{x_2} f(x) dx $$ と表現する。 積分とは「面積」であるから、$X$の確率を図形の面積の大小で言い換えた、と解釈できる。 確率の定義から、$f(x) \ge 0$であり、 $$ \int_{-\infty}^{+\infty} f(x) dx = 1 $$ である。

確率密度関数を使うと、期待値の計算は積分で表現できる。例えば$X$の平均は $$ E[X] = \int x f(x) dx $$ 分散は $$ E[X^2] - E[X]^2 = \int x^2 f(x) dx - \left( \int x\,f(x) dx \right)^2 $$ となる。

デルタ分布

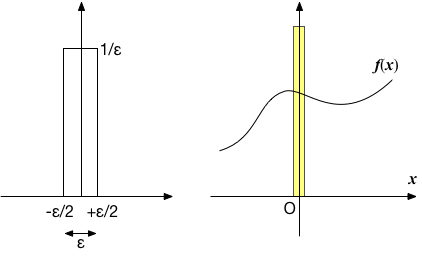
下図のような、0を中心に幅が$\epsilon$、高さが$1/\epsilon$の矩形の形状をした分布を考えてみよう。 $\epsilon$の大小にかかわらず、矩形の面積は1である。 この分布関数を$\delta(x ; \epsilon)$と表記することにする。 そして、別の関数との積を取って積分すると、$f$の不定積分を$F$とすると、 $$ \int \delta(x; \epsilon) f(x) dx = \int_{-\epsilon/2}^{+\epsilon/2} \frac{1}{\epsilon} f(x) dx = \frac{F(\epsilon/2) - F(-\epsilon/2)}{\epsilon} $$ と書くことができる。

$\epsilon \to 0$の極限を取ると、 $$ \lim_{\epsilon \to 0} \frac{F(\epsilon/2) - F(-\epsilon/2)}{\epsilon} = F'(0) = f(0) $$ となる。

ここで、極限を取る順番を入れ替え、あらかじめ $\delta(x) = \lim_{\epsilon \to 0} \delta(x ; \epsilon)$ で定義される分布が与えられていたと考えると、 形式的に $$ \int \delta(x) f(x) = f(0) $$ となる。この$\delta(x)$はデルタ分布（デルタ関数）呼ばれている。デルタ関数は「関数の値を切り出す」作用を持つ。 その定義から明らかに $$ \int \delta(x) dx = 1 $$ および $$ \delta(x) = \delta(-x) $$ が成り立つ。

形式的に上の式の両辺を微分すると、 $$ \frac{d}{dx} \int \delta(x) f(x) dx = \int \delta'(x) f(x) dx + \int \delta(x) f'(x) dx = 0 $$ となるので、 $$ \int \delta'(x) f(x) dx = - \int \delta(x) f'(x) dx = -f'(0) $$ すなわち、デルタ関数の微分を作用させると、関数の微分に負符号を付けた値が切り出される。

デルタ関数 $\delta(x)$ は原点での関数値を切り出す作用をするが、別の場所（ここでは$t$とする）での値を切り出したい場合は、 原点をずらして、 $$ \int \delta(t-x) f(x) dx = f(t) $$ とすればよい。

デルタ関数を使うと、離散的な確率分布も統一的に「関数」として表現できる。例えば、１から６のサイコロの目が等確率で出現する場合の確率密度は $$ f(x) = \frac{1}{6} \left[ \delta(1-x) + \delta(2-x) +\delta(3-x) +\delta(4-x) +\delta(5-x) +\delta(6-x) \right] $$ とすれば良い。

確率変数を「合成」した確率変数の従う分布関数

$X$という確率変数の分布関数$f_X(x)$, $Y$という確率変数の分布関数を$f_Y(y)$とし、$X$と$Y$は互いに独立と仮定する。 ここで、ふたつを加えた $Z=X+Y$ という確率変数が従う確率密度関数はどのように表現できるだろうか。

$Z$が$x+y$を持つような確率は、$X$が$x$、$Y$が$y$という値になる確率（いま互いに独立と仮定しているので$f_X(x)\,f_Y(y)$） の総和のうちで、ちょうど $z=x+y$ すなわち $z-(x+y)=0$ となるようなものを「切り出し」たものである。 デルタ関数の「切り出し」の機能を使うと、これは $$ f_Z(z) = \int \int \delta\left( z - (x+y) \right) f_X(x) f_Y(y) dx dy $$ と表現することができる。

$x$を $t = z - (x+y)$と変数変換すると、 $$ \begin{eqnarray} f_Z(z) & = & \int \int \delta(t) \, f_X(z - t - y) \, f_Y(y) \, dt dy \\ & = & \int f_X(z - y) \, f_Y(y) \, dy \end{eqnarray} $$ となり、$f_X$ と $f_Y$ の畳込み積分として表現できることがわかる。

同じように、$Z=X/Y$の場合は、 $$ \begin{eqnarray} f_Z(z) & = & \int \int \, \delta(z - x/y) \,f_X(x) \, f_Y(y) \, dx dy \\ & = & \int \, f_X(yz) \, f_Y(y) \, |y| \, dy \end{eqnarray} $$ となる。

このように、複数の確率変数で合成された確率変数の従う確率分布関数は、デルタ関数を使うことでうまく表現することができるし、 細かいことをあまり気にせずに計算を進めることができる。

　解説:独立な確率変数の和

任意の実数値を取る独立な確率変数$X_1, X_2, \cdots, X_n$の確率密度が、それぞれ $f_1(x_1), f_2(x_2), \cdots, f_n(x_n)$ であったとしよう。 確率変数の和 $Y = \sum_{i=1}^n$ で合成される確率変数 $Y$ はどのような分布関数で表されるだろうか。 デルタ関数を使った上記の表現方法を使えば、 $$ f_Y(y) = \int_{-\infty}^{\infty} dx_1 \cdots \int_{-\infty}^{\infty} dx_n \; \delta\left( y - \sum_{i=1}^n x_i \right) \prod_{i=1}^n f_i(x_i) $$ となる。

ここで、$f_Y(y)$ のフーリエ変換を考え、デルタ関数の性質を使って、式を変形してみる： $$ \begin{eqnarray} F_y(q) & = & \int_{-\infty}^{\infty} f_Y(y) e^{-iqy} dy \\ & = & \int_{-\infty}^{\infty} dx_1 \cdots \int dx_n \; \delta\left( y - \sum_{i=1}^n x_i \right) \prod_{i=1}^n f_i(x_i) e^{-iqy} dy \\ & = & \int dx_1 \cdots \int dx_n \; \prod_{i=1}^n f_i(x_i) e^{-i q \sum_{i=1}^n x_i } \\ & = & \prod_{i=1}^n \int f_i(x_i) e^{-iqx_i} dx_i = \prod_{i=1}^n F_i(q) \end{eqnarray} $$ ただし、上式では $f_i(x_i)$ のフーリエ変換を $$ F_i(q) = \int_{-\infty}^{\infty} f_i(x_i) e^{-iqx_i} dx_i $$ とおいた。

上の結果は次のようにまとめられる：独立な確率変数の和によって合成される確率変数の確率密度関数は、フーリエ空間（フーリエ変換の像）で考えると、 それぞれの確率変数をフーリエ変換したものの積になっている。

このことを踏まえると、独立な確率変数の和が従う確率密度関数は、一般的に以下の手順で得らことができる：

1. $f_i(x_i)$のフーリエ変換 $F_i(q)$ を計算する
2. それらの積が $f_Y(y)$ のフーリエ変換となる： $F_Y(q) = \prod_{i=1}^n F_i(q)$
3. $F(q)_Y$ をフーリエ逆変換して、$f_Y(y)$を求める

その具体的な計算例を、ガウス分布（中心極限定理）や、ランダウォークの説明に用いているので参照のこと。

　解説:デルタ分布のフーリエ変換

デルタ分布（ディラックのデルタ関数）$\delta(x)$のフーリエ変換を使った表現 $$ \delta(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} e^{iqx} dq $$ は計算に便利であるため、よく用いられる。オイラーの公式 $$ e^{iqx} = \cos(qx) + i \sin(qx) $$ から、 $$ \delta(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \cos(qx) dq + \frac{i}{2\pi} \int_{-\infty}^{\infty} \sin(qx) dq $$ と書いても同じことである。 この式は、「いろいろな波長の波を無数に重ね合わせるとデルタ分布に近づく」ことを示しているが、 その様子を実際に実験で観察してみよう。

# coding: utf-8                                                                                                                                                     
import numpy as np
import matplotlib.pyplot as plt

x = np.arange(-np.pi, np.pi, 0.01)
sc = np.zeros(x.shape[0])
ss = np.zeros(x.shape[0])
dq = 0.01
qlist = np.arange(-100, 100, dq)
for q in qlist:
    sc = sc + np.cos(q*x)*dq
    ss = ss + np.sin(q*x)*dq

sc = sc/(2*np.pi)
ss = ss/(2*np.pi)
plt.plot(x, sc, '-', color='red')
plt.plot(x, ss, '-', color='blue')
plt.show()

$q$を$(-100,100)$の範囲で変えながら、$\cos(qx)$と$\sin(qx)$を加え合わせるだけのシンプルなコードである。 以下のプロットが実行結果の例で、赤が実部、青が虚部になる。 $\cos(qx)$は、$x=0$でのみ位相が揃うので大きなピークを呈するが、$x$の他の値では異なる位相の値が打ち消しあう様子が見て取れる。

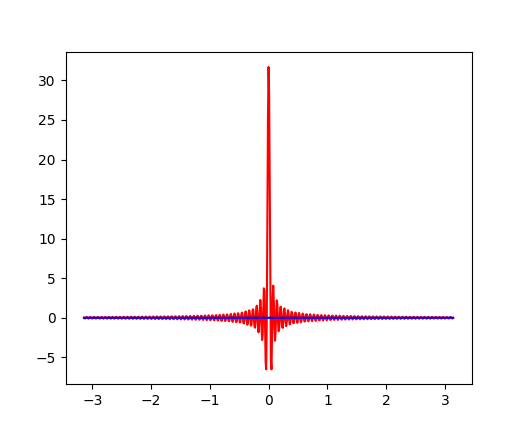
このシミュレーションから、確かに余弦関数の「重ね合わせ」が鋭いピークを呈するようであることは確認できるが、 その尖った分布が $$ \int_{-\infty}^{\infty} \delta(x) dx = 1 $$ を満足しているのかについて、もう少し考えてみよう。

正の数 $Q$ について $$ w_Q(x) = \frac{1}{2 \pi} \int_{-Q}^Q \cos(qx) dq = \frac{1}{\pi} \frac{\sin(Qx)}{x} $$ とおくと、$Q$には依らず $$ \int_{-\infty}^{\infty} \frac{\sin(Qx)}{x} dx = \pi $$ であることから† $$ \lim_{Q\to\infty} \int_{-\infty}^{\infty} w_Q(x) dx = \int_{-\infty}^{\infty} \delta(x) dx = 1 $$ すなわち、上図の赤い線に囲まれた部分の面積は確かに1になることが分かる。

† sinc関数の積分の評価