情報基礎「Pythonプログラミング」（ステップ６：数値積分）

Pythonプログラミング（ステップ６・数値積分）

このページの目標

積分を「総和計算のパターン」に当てはめることで、数値積分のアルゴリズムを理解し、コードに反映できること。
計算誤差が生じる理由、とくに丸め誤差について、意識すること。

台形法による数値積分

数学を勉強してみて分かるのは、ちょっと複雑な関数になると、積分を計算するのはとても難しくなること、そして、解析的にその積分を求めることができないような関数もたくさんある（そんなのばかりである）ことだ。その一方で、理工学的には積分値を求めなければならない場面が沢山ある。

　解説:台形法による積分の計算

積分は「面積」を求める問題である。そこで、関数 $f(x)$ の区間 $(a,b)$ での定積分を、それをよく近似する多角形（台形:trapezoid）の面積の総和を求める問題としてとらえ直してみよう。すると、作戦としては、こんな感じでいけそうだ（台形法）：

下図のように、区間$(a,b)$ を $n$ 等分（下図では$n=8$）して、１つの区間の幅が$\Delta x = (b-a)/n$ となるような台形状の短冊を作る。
例えば、緑色の部分の台形の面積は $( f(x_1)+f(x_2) ) \, \Delta x / 2$ である。
全ての区間について、台形の面積を求め、その総和を求めれば、その値は積分（面積）をよく近似しているだろうし、$\Delta x$ を小さくすれば、さらに近似の精度は高まるであろう。

このアイデアを素直にPythonで表現すると、以下のようになるであろう(trapezoidal.py)。ここでは、被積分関数として、正弦関数(sin()）を設定してある。

trapezoidal.py

# coding: utf-8
import math

a,b=map(float,input("積分の上限と下限を入力:").split())
n=int(input("分割数を入力:"))

dx=(b-a)/n  # 「短冊」の幅
s=0         # 総和を求めるための変数
for i in range(0,n,1):
    x1=a+dx*i
    x2=a+dx*(i+1)
    f1=math.sin(x1)
    f2=math.sin(x2)
    s=s+(f1+f2)*dx/2

print("積分結果=",s)

このプログラムを実際に動かして動作を確認してみること。例えば、a=0, b=3.1415926, n=100と設定したら、積分の厳密な値(=2)を正しく求めることができるだろうか。あるいは、sin()のところを、他の関数に置き直して、動作を確かめてみるのも良いだろう。

　練習：台形法プログラムのシェイプアップ

$f_n=f(x_n)$と略記した。

上記の台形法の計算プログラムは、面積の総和を求める部分でちょっと無駄な計算をしている。プログラムが実際に計算しているのは、以下のような式である（方式１） $$ s = \frac{\left( f_0 + f_1 \right) \Delta x}{2} + \frac{\left( f_1 + f_2 \right) \Delta x}{2} + \frac{\left( f_2 + f_3 \right) \Delta x}{2} + \cdots + \frac{\left( f_{n-1} + f_{n} \right) \Delta x}{2} $$ この計算方法は完全に正しいのだけれども、計算の順序を入れ替えて、 $$ s = \left[ \frac{f_0}{2} + f_1 + f_2 + \cdots + f_{n-1} + \frac{f_n}{2} \right] \Delta x $$ を計算しても、結果は全く変わらないはずだ（方式２）。しかも、式はえらく簡単になってしまっていて、

端っこの２点だけ、関数の値に1/2をかけた値を総和に加える
その他の点では、単純に、その点での関数の値を総和に加える
求めた総和に、短冊の幅（$\Delta x$)を（一回だけ）かける

という、単純なステップで計算が完了してしまう。かけ算の回数は、たった１回に減ってしまった。

以上を踏まえて、上の「方式２」で積分を計算するよう、例題プログラム(trapezoidal.py)を改修してみなさい。

発展練習

台形法に似た計算方法に中点法(midpoint method)がある。そのアイデアは単純で、短冊の面積を中点の関数値を使って $$ f\left(\frac{x_i + x_{i+1}}{2}\right) \Delta x $$ で近似するというものだ（$\Delta x$は短冊の幅）。台形法のプログラムを元に、中点法のコードを作成し、動作を確認してみなさい。

数値計算アルゴリズムのさらなる検討

前節では、同じ台形法という方法の中であっても、プログラム上の計算の順序などには工夫の余地があって、計算コストがかなり減らせる場合があることを示した。さらに考えを進めて、精度を向上させたり、計算効率を上げるために、計算アルゴリズム自体を改良する努力も、綿々と続けられている。例えば、台形則のバリエーションのひとつである二重指数関数(DE)型公式についてこちらのページで説明した。以下では、台形法の発展型として、関数を線分ではなくて２次曲線で近似する方法を紹介しておこう。

　解説:シンプソン公式

積分を計算する際に、短冊毎の面積 $S_i$ を、台形の面積としてではなくて、以下で近似する方法をシンプソン則（Simpson's rule）と呼ぶ。

$$ S_i = \frac{\Delta x}{6} \left[ f(x_i) + 4 f\left(x_i + \frac{\Delta x}{2} \right) + f\left( x_i + \Delta x \right) \right] $$

このシンプソンの公式を使うと、同じ短冊の幅 $\Delta ｘ$ に対して、より高い精度で面積（積分）を求めることができる。

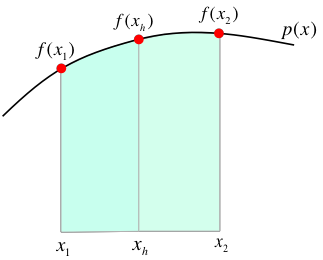
ここで、簡単に、この公式の導出方法を述べておこう。台形公式では、それぞれの短冊での関数の変化を線分（1次式）で近似したが、シンプソンの公式は、それを2次関数で近似したものである。なめらかに変化する関数を、なめらかな（二次）曲線で近似するのだから、一般に、実際の値により近い見積もりを得ることができるはずだ。ここで、下図のように $(x_1, x_2)$の区間の短冊を考えよう。

その中点を $x_h=(x_1+x_2)/2$ とする。ここで、$(x_1,\ f(x_1)$, $(x_h,\ f(x_h))$, $(x_2,\ f(x_2))$の三点（図の赤い点）を全て通る二次関数 $p(x)$ は一意に決めることができて（ラグランジュの補間公式）、この $p(x)$ は $f(x)$ のより良い近似になっているはずである。

$$ p(x) = \frac{(x-x_h)(x-x_2)}{(x_1-x_h)(x_1-x_2)} f(x_1) + \frac{(x-x_1)(x-x_2)}{(x_h-x_1)(x_h-x_2)} f(x_h) + \frac{(x-x_1)(x-x_h)}{(x_2-x_1)(x_2-x_h)} f(x_2) $$

$p(x)$ は $x$ について2次式に過ぎないから、これを（解析的に）積分するのは容易で、式を整理するとシンプソン則

$$ \int_{x_1}^{x_2} p(x) dx = \frac{x_2-x_1}{6} \left[ f(x_1) + 4 f(x_h) + f(x_2) \right] \tag{1} $$

が得られる。このように、短冊内での関数の変化を等間隔な分点での関数値を使った多項式で近似し、積分を求めるタイプの公式を、ニュートン・コーツ型の積分公式と呼ぶ。

参考: 公式の導出もPythonで

シンプソン則の導出はそれほど難しい計算ではないものの、検算のためにPythonを用いるのも有用かもしれない。以下は、sympyを使って(1)式の積分計算を行わせる例である：

実行するにはsympyを追加インストールする必要がある。

行末のバックスラッシュ（\）は、その行が次に継続していることを表す。

# coding: utf-8
from sympy import *
init_printing()

x,x1,x2 = symbols("x x1 x2")
f1,fh,f2 = symbols("f1 fh f2")

xh=(x1+x2)/2

p = (x-xh)*(x-x2)*f1/((x1-xh)*(x1-x2)) \
  + (x-x1)*(x-x2)*fh/((xh-x1)*(xh-x2)) \
  + (x-x1)*(x-xh)*f2/((x2-x1)*(x2-xh))

res = simplify(integrate(p,(x,x1,x2)))
print(collect(factor(res),(f1,fh,f2)))

　練習：シンプソン法による数値積分プログラム

台形法の積分プログラムを元にして、シンプソン法による計算プログラムを書いてみなさい。同じ区間、同じ分割数で、同じ関数の場合に、台形法とシンプソン法との積分値を比べてみよ。特に分割数が少ない（短冊の幅が大きい）場合の、結果の「悪くなり方」はどうか。

計算誤差についての配慮

　解説:丸め誤差

台形法では、短冊状の領域を台形で近似することによる誤差が生じる。この誤差を減らすには、短冊の幅を小さく（＝分割数を多く）すれば良さそうだが、それにも限界はある。台形法に限らず、面積を求めるプログラムの中心部分は

   s=0
   for i in range(0,n,1):
      s = s + （i番目の短冊の面積）

のような構造をしている。ここでsの値に比べて、短冊の面積が極端に小さいとすると、例えば

1.23456789012345 + 0.0000000000000123456789012345

のような計算を繰り返すことになるだろう。ところが、計算機で表現できる実数の有効数字はfloat型でおよそ7桁、double型でも15桁程度しかない。そうすると、上記のように、相対的な桁数が大きく異なる数の間で、和や差を計算すると、有効数字（計算精度）が極端に悪くなってしまうだろう（下図のように、足したはずなのに値が変化しない、等々）。このように、数値の精度に起因する計算上の誤差を丸め誤差（round-off error）と呼ぶ。

短冊の幅をあまり小さくできないとすると、積分の精度をさらに向上させるには、別の工夫が必要となる。基本的な考え方として、（線分近似ではなくて）関数が滑らかに変化する様子まできちんと考慮することで、計算精度を向上させることが可能だが、ここから先は、この講義の範囲外なので、学年が進んでから「数値解析」に関係した講義で勉強してほしい。

一般に、丸め誤差の影響を深刻化させないためには

物理シミュレーションの場合は、方程式などをあらかじめ無次元化し、極端に大きな（小さな）数が現れないように問題を「仕込んで」おく。
計算の順序、アルゴリズムを精査し、桁数が極端に離れた数値同士の和や差の計算を行わないようにする。

などの配慮が必要となる。

　練習：数列の和

ゼータ関数 $\zeta(2)$ の値を、項を加える順序を変えただけの、 $$ \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \cdots + \frac{1}{N^2} $$ と $$ \frac{1}{N^2} + \cdots + \frac{1}{3^2} + \frac{1}{2^2} + \frac{1}{1^2} $$ （$N \to \infty$)の二通りのやり方で近似計算するプログラムを作成し、結果を比較してみなさい。