Pythonプログラミング（ステップ７・補足・ガンマ関数）

このページでは、統計分布などにしばしば登場するガンマ関数について説明する。

積分で定義されるガンマ関数

積分を使って「新しい」関数を定義する例はたくさんある。 例えば、正規分布$\frac{1}{\sqrt{2\pi}} e^{-t^2/2}$ を元に、その累積分布関数 $$ F(x) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^x e^{-t^2/2} dt $$ を定義できるが、$F(x)$をこれ以上簡単な数式で表すことはできない。

これは、積分範囲を「可動」にして、関数を生成する例であるが、 被積分関数の中に「可動」な変数を入れて、関数を生成することもできる。 その代表的な例がガンマ関数で、以下のように定義される： $$ \Gamma(z) = \int_0^{\infty} t^{z-1} e^{-t} dt $$ 被積分関数の中身の$z$が「可動」箇所で、$t$で積分しても、その部分の自由度が残るため、積分全体としては$z$の関数となる。

階乗の一般化

では、ガンマ関数の値を計算してみよう。 $z=1$の場合は $$ \Gamma(1) = \int_0^{\infty} e^{-t} dt = \left[ -e^{-t} \right]_0^{\infty} = 1 $$ $z=1/2$の場合は、$t = y^2$と変数変換すると $$ \Gamma(1/2) = \int_0^{\infty} t^{-1/2} e^{-t} dt = 2 \int_0^{\infty} e^{-y^2} dy = \sqrt{\pi} $$ と求まる。 その他の一般の $z$ に対しては値を求めることが難しい。

しかしながら、$z$が自然数の場合と、半整数の場合は、具体的な値を得ることができる。 まず、部分積分($e^{-t}$を積分、$t^{z}$を微分）すると、 $$ \begin{eqnarray} \Gamma(z+1) = & \int_0^{\infty} t^{z} e^{-t} dt = \left[ -t^z e^{-t} \right]_0^\infty + \int_0^{\infty} z \, t^{z-1} e^{-t} dt \\ & = z \int_0^{\infty} t^{z-1} e^{-t} dt = z \, \Gamma(z) \end{eqnarray} $$ という関係式（漸化式）が得られる。それを繰り返し適用すると、$n$が自然数の場合 $$ \Gamma(n+1) = n \Gamma(n-1) = n (n-1) \Gamma(n-2) = \cdots = n (n-1) (n-2) \cdots \Gamma(1) = n! $$ となる。すなわち $\Gamma(n+1)$ は $n!$ を与えることがわかった。 同様に、半整数に対しても $$ \Gamma\left( \frac{2n+1}{2}\right) = \frac{2n-1}{2} \frac{2n-3}{2} \cdots \Gamma(1/2) $$ となるので、具体的な値を得ることができる。

ガンマ関数の近似：スターリングの式

統計学や物理学などでは、大きな$n$に対する階乗($n!$)の振る舞いを知る必要性が出てくる。 そこで、$n!$の良い見積を得るために、その積分表示である$\Gamma(n+1)$を使ってみよう。 積分変数を$t = zs$と変換すると $$ \begin{eqnarray} \Gamma(z+1) = \int_0^\infty t^z e^{-t} dt = \int_0^\infty (sz)^z e^{-sz} z ds\\ = z^{z+1} \int_0^\infty s^z e^{-sz} ds = z^{z+1} \int_0^\infty e^{z (\log(s) -s)} ds \end{eqnarray} $$

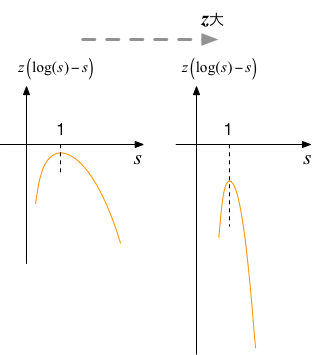
ここで、$e$の「上」の $z(\log(s)-s)$ は上に凸な形をしており、微分を取ると、$s=1$で最大になることがわかる。 これを、$s=1$の周りでテイラー展開すると $$ z(\log(s)-s) = -z - \frac{z}{2} (s-1)^2 + \cdots $$ である。そこで、 $$ \Gamma(z+1) = z^{z+1} e^{-z} \int_0^\infty e^{- \frac{z}{2} (s-1)^2 + \cdots} ds $$ と書き直して、$z$が正の大きな値の場合の積分の振る舞いを考えてみる。

$z$が十分大きければ、被積分関数は$s=1$の周りで鋭いピークを持つので、その値は以下の式でよく近似できるであろう： $$ \int_0^\infty e^{- \frac{z}{2} (s-1)^2 + \cdots} ds \approx \int_{-\infty}^\infty e^{- \frac{z}{2} (s-1)^2} ds = \sqrt{\frac{2\pi}{z}} $$ ピークの幅が鋭くなれば、「遠く」の様子は関係なくなるであろうから、積分範囲を$-\infty$まで広げても結果は変わらないはずである。 また、展開の高次の項も無視できるとした（本来ならば誤差の評価を行うべきであるが、ここでは割愛）。

ここまでをまとめると、スターリングの式として知られる $$ n! = \Gamma(n+1) \approx n^{n+1} e^{-n} \sqrt{\frac{2\pi}{n}} = n^{n+1/2} e^{-n} \sqrt{2\pi} $$ が得られた。

Pythonでは、ガンマ関数は数学ライブラリとして用意されており、積分を行わずとも、import math しておけば、math.gamma( )で呼び出すことができる。以下に、ガンマ関数の値とスターリングの近似値のそれぞれ対数を計算し、比較してプロットするコードの例を示す。

# coding: utf-8

import matplotlib.pyplot as plt
import numpy as np
import math

xdata = np.arange(1,10,0.01)
n = xdata.shape[0]

log_gamma = np.empty(n)
log_stirling = np.empty(n)

for i in range(n):
    x = xdata[i]
    log_gamma[i] = math.log(math.gamma(x+1))
    log_stirling[i] = (x+1/2)*math.log(x) - x + 1/2*math.log(2*math.pi)

plt.title("GAMMA FUNCTION")
plt.plot(xdata,log_gamma, color=(1.0,0,0.0), linewidth=1.0)
plt.plot(xdata,log_stirling, color=(0.0,0,1.0), linewidth=1.0)
plt.xlim(0,10)
plt.xlabel('X')
plt.ylabel('LOG GAMMA(X)')
plt.grid(True)
plt.show()

ベータ関数

ガンマ関数の親戚で、統計学などでよく登場する二変数の関数にベータ関数がある。 ベータ関数はいろいろな定義（表現）が可能であるが、ひとまず、ガンマ関数との関係 $$ B(x,y) = \frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)} $$ を押さえておけば、Pythonのmathライブラリを使って、

math.gamma(x)*math.gamma(y)/math.gamma(x+y)

で計算が可能である。