Pythonプログラミング(ステップ3・選択処理)
このステップの目標
- 分岐構造とプログラムの流れを的確に把握できる
- if文を使って、分岐のあるフローを記述できる
- Pythonの条件式を正しく記述できる
1. 分岐のあるプログラムと選択処理
二次方程式を解くプログラム(ex3.py)
二次方程式 $a x^2 + b x + c = 0$ の係数 $a,b,c$ を与えると、判別式を評価し、実数解を表示するプログラムの例を以下に示す:
例題3(ex3.py)
![]()
# coding: utf-8
import math
a,b,c=map(float,input("係数 a b c を入力してください:").split())
d=b*b-4*a*c
if d<0:
print("実数解はありません")
else:
s1=(-b+math.sqrt(d))/(2*a)
s2=(-b-math.sqrt(d))/(2*a)
print("答え:",s1,s2)
例題3のアルゴリズム
Input: 2次方程式の係数 $a,b,c$
Output: 2次方程式の2つの実数解
1: 画面に"係数a b cを入力してください:"と出力し、改行する
2: キーボードから3つの実数を入力し、それぞれ変数 $a, b, c$ にセットする
3: 実数の変数 $d$ に $b^2 - 4 a c$ の値をセットする
4: もし $d \lt 0$ ならば以下を実行する:
5: "実数解はありません"と出力し、改行する
6: それ以外($d \ge 0$)の場合は以下を実行する:
7: 変数 $s_1$ に $\frac{-b + \sqrt{d}}{2 a}$ の値をセットする
8: 変数 $s_2$ に $\frac{-b - \sqrt{d}}{2 a}$ の値をセットする
9: "答え: "に続いて、$s_1, s_2$ の値を出力し、改行する
10: 条件分岐はここまで
11: 終了する
プログラムを実行すると、二次方程式の係数の値を尋ねられるので、三つの数値を順にタイプしてEnterキーを押すと、実数解が(もしあれば)表示される。
 if文を使った条件分岐(選択処理)
if文を使った条件分岐(選択処理)
if文
2次方程式の解の求め方が、判別式の正負で異なるように、処理(計算)の内容を条件によって切替なければならない類の問題に、我々はしばしば遭遇する。 その際に、「切り分け」を行うのがif 文である。
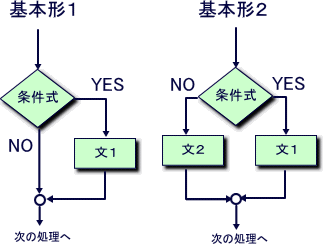
if文には大きく二つの基本形がある。
if 条件式: 文1if 条件式: 文1 else: 文2
この基本形の中で、文1 や 文2 の個所は、複文(ブロック)でも構わない。ブロックとは
何々1
何々2
何々3
...
のように、字下げのレベルを揃えた文の集まりのことであった。すると、例題3は基本形2をひとつ含む例であることがわかる。
それぞれの基本形を流れ図で示すと以下のようになる;
条件式
基本形の条件式のところには、処理の流れを切り替えるための条件を、下表のような論理式のかたちで記述する。
そして、その「真」,「偽」に応じて、流れがコントロールされる。
表中で、a,bのところには、変数だけでなく、数式を記述することもできる。
条件式の次には、コロン : が必要である。
| 書き方 | 内容 |
|---|---|
a == b |
aとbが等しければ・・・ 等号(=) 2つであることに注意 等号ひとつ(=)は「代入」と解釈され、全く意味が異なる。 |
a < b |
bが大きければ・・・ |
a > b |
aが大きければ・・・ |
a <= b |
bがaより大きいか,等しければ・・・ " =< " はNG |
a >= b |
aがbより大きいか,等しければ・・・ " => " はNG |
a != b |
aとbが等しくなければ・・・ |
例題3のその他の見所
- bの2乗は
b*bと書いても良いし、Pythonではb**2のような書き方も可能である - 平方根は math.sqrt(式) で表現(sqrtはSQuare RooTの略)。これを使うときは、プログラムの宣言部に
import mathを忘れずに書いておく。 (-b + math.sqrt(d))/(2*a)と(-b + math.sqrt(d))/2*aは結果が異なる。数式中の括弧の使い方に注意。
 if文の組み合わせによる複雑な分岐処理
if文の組み合わせによる複雑な分岐処理
例題3のプログラムは、係数aに0を入れると(一次方程式の場合は)、解の公式の分母が0になってしまうので、正しく計算を行うことができない。 そんな場合にも対応するには、aが0の場合と、それ以外の場合で、処理方法を変えなければならない。具体的には、
もしaが0ならば、一次方程式の解を求める そうでなければ(aが0以外ならば)、以下の処理を行う: もし判別式が負値ならば、実数解なし そうでなければ、解の公式で二つの実数解を求める
といったアルゴリズムになるはずだ。これをPythonコードに「翻訳」すると、
さらに細かいことを言えば、bが0の場合も場合分けする必要がある。
if a==0:
s1 = -c/b
print("答え:",s1)
else:
if d<0:
print("実数解はありません")
else:
s1 = (-b + math.sqrt(d))/(2*a)
s2 = (-b - math.sqrt(d))/(2*a)
print("答え:",s1,s2)
となる。if文の基本形2のelseの「内部」に、さらに基本形2のif文が挿入されている点に注目。
if〜elif〜else
elif: = else: if による記述
if文の基本形2で、
if 条件式1:
文1
else:
if 条件式2:
文2
else:
if 条件式3:
文3
...
else:
文4のように分岐が多くなると、インデントが深くなって分かりづらくなるので、
if 条件式1: 文1 elif 条件式2: 文2 elif 条件式3: 文3 ... else: 文4
のようなelif を使った書き方が良く用いられる(二つは全く同様の動作をする)。 else と if を連結してしまって elif にした、といったイメージである。 こちらも基本形2のバリエーションと考えることができる。
 練習:重根および虚数解にも対応できるプログラム
練習:重根および虚数解にも対応できるプログラム
例題2を元に、重根($d=0$)の場合には、根をひとつだけ出力するようにプログラムを改良してみなさい。
余力があれば、さらに $d \lt 0$ (虚数解)の場合であっても、"実部 + 虚部 i" のように計算結果が表示されるよう、プログラムを拡張してみなさい。
 ヒント
ヒント
実部と虚部をそれぞれ別個に計算しておいて、print(real1,"+",imag1,"i") ; のように表示すれば良さそうだ。
その際、追加の変数が必要であれば、適宜宣言すること。
発展:三次方程式
さらなる発展として、三次方程式の解の公式(カルダーノの公式等)を使って、
三次方程式を解く(とりあえずは、実数解のみ)プログラムに挑戦してみるのも面白いだろう。
式の途中で、三乗根の計算が必要になる。実数変数xの三乗根はx**(1.0/3.0)、または、math.pow(x,1.0/3.0)と表現すればよい
(math.pow(x,y)は$x^y$を表す関数)。
2.複雑な分岐条件の記述
上の節では、if文の構成方法にフォーカスを当てたが、条件式の書き方にも、色々なバリエーションが可能だ。
| 書き方の例 | コメント |
if a+b > c+d: |
数式の計算結果同士の比較の例 |
if k%2: |
ここでkはint型と仮定。k%2は、kを2で割った余り。 kが偶数の場合はk%2は0を、奇数の場合はk%2は1を与える。 Python言語の条件式では、整数式の結果が0の場合は「偽」を、 それ以外(例えば1)の場合は「真」と解釈される。 つまり、この例は、「もしkが奇数ならば・・・」の書き方のバリエーション。 |
if a*a + b*b == c*c: |
a,b,cがint型の場合には、見てのとおりの条件式。 a,b,cがfloat型の場合(授業で説明はしていないがdouble型の場合も)、この条件式は 意図した通りに働かない可能性が高い。というのは、コンピュータは実数の 近似値を計算しているだけなので、数学的には等号が成立する場合でも、 誤差によって、計算機の内部では両辺が「完全に」等しい保証がないからだ。 例えば、 if math.sqrt(x)**2==x:は、xの値によっては「偽」になってしまう。
|
 複雑な条件式
複雑な条件式
論理積(かつ)、論理和(または)、否定(でない)
込み入った条件を記述しようとすると、以下のように、論理積(「かつ」)、論理和(「または」)、論理否定(「・・でない」)の組み合わせ が必要になることも多い。ここでは、以下の3つの基本的なパターンをきっちりと押さえておこう:
| 条件 | 書き方の例 | コメント |
| A かつ B |
a > b and b > c |
andで「かつ」を表す。 Pythonでは左の例を a > b > c と書くことも可能。 |
| A または B |
a > b or a > c |
or で「または」を表す。 |
| A ではない |
not (a > b) |
not は、その右側の条件式の否定(negation, not)。 否定すべき範囲を括弧で囲むこと。 |
 練習:数値の並べ替え
練習:数値の並べ替え
キーボードから3つの実数を入力すると、それを小さい順(昇順)に並べ替えた上で表示するプログラムを作成してみなさい。 こちらの課題で考えたアルゴリズムをPythonコードに翻訳すればよい。
# coding: utf-8
x,y,z=map(float,input("x y z:").split())
・・・・・
printf("x= %f y=%f z=%f\n",x,y,z) ;
|
 練習:三角形の分類
練習:三角形の分類
三角形の三辺の長さを入力すると、それが鋭角三角形(acute triangle)か、直角三角形(right triangle)か、鈍角三角形(obtuse triangle)かを判別し、結果を出力するプログラムを作成しなさい。
 ヒント
ヒント
三辺の長さを $a,b,c$ としたとき、$a$ が最も長い辺の場合は、$a^2 \lt b^2 + c^2$なら鋭角、$a^2 \gt b^2 + c^2$なら鈍角、 $a^2 = b^2 + c^2$ なら直角三角形ということになる。 だが、入力された3つの数値のうち、いつも $a$ が最長になっているとは限らない。 そこで、まず $a$ が最長になるように並べ替えてから、$a^2$ と $b^2+c^2$ の大小関係を評価すればよい。 その際、$b \gt c$である必要はない。
# coding:utf-8
a,b,c=map(float,input("a b c:").split())
# 辺の長さの並べ替え(aが最長になるように)
?????
...
# 確認ステップ
print("並べ替え後の辺の長さ: a=",a,"b=",b,"c=",c) ;
# 三角形の分類と結果の出力
?????
...
|
 練習:三角形の面積計算(チェック機能付き)
練習:三角形の面積計算(チェック機能付き)
ステップ2の練習課題で、 三角形の3辺の長さa,b,cから、その面積Sを計算するプログラムを作成した。 そのときは、あまり気にしなかったけれども、a,b,cの組をあまりいいかげんに設定すると、そもそも 三角形が構成できないので、面積を計算すること自体に意味が無くなってしまうだろう(そして、ヘロンの公式の根号の中が負になってしまう)。 そこで、入力したa,b,cが三角形を構成できない場合には「三角形が構成できません」と表示して終了するように、 面積計算のプログラムを拡張してみなさい。
 ヒント
ヒント
三角形が構成できる条件は、全ての点の組み合わせについて三角不等式(triangle inequality) $a+b>c,\; b+c > a,\; c+a>b$ が(いずれも)成り立つこと。 一般に、(その意図のある無しに関わらず)間違ったデータを入力された場合を想定して、 あらかじめエラー回避を行う処理を仕込んでおく配慮が大切だ。
三角形が構成できないような辺の組合わせでヘロンの公式を使うと、平方根関数の(math.sqrt( ))中が負になってしまう。
こうした際には、当然、結果を数値として表現できないから、"ValueError: math domain error" というエラーメッセージと共に、プログラムは停止する。
 発展練習:うるう年の判定
発展練習:うるう年の判定
参考:暦の計算の基本事項
西暦年を入力すると、グレゴリオ暦(Gregorian calendar)に従って、それがうるう年(leap year)かどうかを判定し、「平年です」または「うるう年です」のように出力するプログラムを作成しなさい。
 ヒント
ヒント
地球の公転周期は約365.2422日であることが分かっている。 現在採用されているグレゴリオ歴では、 基準となる日数を365日として、西暦年が
- 4で割り切れたら +1 日 (4年に1度の+1日調整、すなわち 1年あたり +1/4 日の調整)
- 100で割り切れたら -1日(100年に1度の-1日調整、すなわち 1年あたり -1/100 日の調整)
- 400で割り切れたら +1日(400年に1度の+1日調整、すなわち 1年あたり +1/400 日の調整)
のルールで調整し、平均的な1年の長さが、実際と非常に近い、$365 + \frac{1}{4} - \frac{1}{100} + \frac{1}{400} = 365.2425$ 日となるように工夫されている。 そして、うるう年とは、『調整日数が 0 日以外』であるような年のことである。 ただし、『調整日数が0日以外』は、『4で割り切れる または 100で割り切れる または 400で割り切れる』を意味しないことに注意。 何故なら、調整日数が +1-1=0 となる組み合わせもあるからである。
詳しくは、暦の計算の基本事項を参照のこと。
剰余
yが4で割り切れるかどうかを判断するには、
if year%4 == 0: ・・・ といった具合に、整数の剰余を計算する演算子%を使えばよい。たとえば
8%4は0を与え、 9%4は1、 10%4は2を与える。
(なお、負の数の剰余の定義は言語処理系によって流儀が異なる場合があるので、注意が必要である。)
以下に、出発点となるひな形を示しておく:
# coding: utf-8
year = int(input("year ?"))
if ....
?????
...
|
発展:曜日の計算
暦と日付の計算の説明を読んで、西暦年月日(y, m, d)を入力すると、 その日の曜日を出力するプログラムを作成しなさい。
 亀場で練習:三角形の描画(チェック機能付き)
亀場で練習:三角形の描画(チェック機能付き)

以前に作成した三角形の描画プログラムを改良し、 3辺の長さa,b,cを与えると、三角形が構成可能な場合は、 直角三角形ならば白、鋭角三角形ならば青、鈍角三角形ならば赤色で、亀場に描くプログラムを作成しなさい。 また、もし三角形が構成できない場合は、"NO SUCH TRIANGLE" と亀場に表示するようにしなさい。
 ヒント:
ヒント:
線分の色を変えるには、pd() でペンを下ろす前に col() 関数を呼び出す。
色の使用について、詳しくはこちらのページを参照のこと。
また、亀場に文字列を描くには say("ABCEDFG...") 関数を使う。