亀場でプログラミング:色情報の表現
このページでは、「色」についてあれこれ考えてみたい。
1. 色覚とそのデータ表現
我々の目の網膜には、明暗に反応する細胞(桿体(かんたい)細胞)と、異なる光の波長に選択的に反応する3種類の細胞(L,M,およびS錐体細胞)がびっしりと並んでいる。 そして、網膜上に結んだ光の像に反応して、これらの光センサーから送られてきた信号を脳内で統合することによって、「色」を感じているわけだ。 3種類の錐体細胞は、それぞれ、長い波長(赤)、中くらいの波長(黄緑)、短い波長(青色)に感度のピークがある。 この、赤(R)、緑(G)、青(B)は、光の三原色に対応しており、この(R, G, B)のブレンドの具合で、さまざまな色が表現できる。
(R,G,B)の表現で、1を最大の光量とすれば、(1,1,0)は黄色、(0,1,1)は水色、(1,0,1)はマゼンタ、(1,1,1)は白、そして、(0,0,0)は黒、ということになる。
光の三原色と、その混合

単色光にさらに赤成分を追加しないと、(R,G,B)で表現した色と同じに見えないような場合、 形式上「R成分がマイナス」とみなす。
そうすると、全ての色は(R,G,B)だけの組み合わせで表現できるのかと言うと、事情はそれほど単純ではない。 CIE 1931 rbg表色系では、 Rとして700 nm, Gは546.1 nm、Bは 435.8 nmの3種類の単色の組み合わせで、色の表現が試みられている。 ところが、単色の光の波長を変化させながら、それと「同じ色」に見えるような(R,G,B)の混合率を調べてみたところ、 どんな風に三つの原色をブレンドしても表現できない色があることが分かっている(形式的には、赤の光の強度がマイナスになってしまう)。
2. タートルグラフィックスでの色指定
亀場のタートルグラフィックスで色を指定する関数は2つある:一つは、線の色を指定するためのCOL()、もう一つは
背景色を指定するためのBGC()関数である。
いずれも、R, G, Bの光の強度を0から1の範囲で指定する。
初期状態では、線分の色は赤(1,0,0)、背景色は黒(0,0,0)が設定されている。
線分の色指定の基本は、PD()でペンを下ろす前にCOL()関数を呼び出すことだ。すなわち、
COL(赤,緑,青); PD(); FD(距離); PU();
の順に関数を呼び出せば良い。
線分を続けて描く場合に、色は、線分の各頂点に対して指定することができる。 例えば、各頂点に異なる色を指定しながら線分を描画すると、
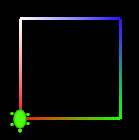
COL(1,0,0); /* 始点の色 赤 */ PD(); COL(0,1,0); /* 次の頂点 緑 */ FD(100); LT(90); COL(0,0,1); /* 次の頂点 青 */ FD(100); LT(90); COL(1,1,1); /* 次の頂点 白 */ FD(100); LT(90); COL(1,0,0); /* 次の頂点=始点 赤 */ FD(100); PU();
左図のように、頂点の色が連続的に補間されて表示される。
FD()する前に設定した色が、次の頂点の色となる。
同じコードをFILL(塗りつぶし)モードに変更して実行すると
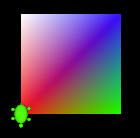
FILL(); /* 塗りつぶしモードを設定 */ COL(1,0,0); /* 始点の色 赤 */ PD(); COL(0,1,0); /* 次の頂点 緑 */ FD(100); LT(90); COL(0,0,1); /* 次の頂点 青 */ FD(100); LT(90); COL(1,1,1); /* 次の頂点 白 */ FD(100); LT(90); COL(1,0,0); /* 次の頂点=始点 赤 */ FD(100); PU();
図のように、面領域で色が補間されて表示される。このように、頂点を色を変えることで、 グラデーションの効果を出すことも可能である。
 練習:虹のシミュレーション
練習:虹のシミュレーション
虹は大気中の水滴がプリズムの役割を果たして、太陽の白色光が波長の異なる光に分解されるため、あのような色の帯となって「見える」。 そのこと自体は、大学生なら誰でも知っているとおりなのだけれど、プリズムで分けられた単色光が実際にどんな色に感じられるのかは、 ちょっと想像が難しい。
そこで、可視光領域(ここでは波長$\lambda$が400 nm から 650 nmの範囲を考えよう)の単色光の色を表示する プログラムを作って、実際にその色を確認してみよう。言うならば、虹のシミュレーションである。
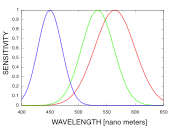
波長$\lambda$(nm)に対する3つのセンサー(L,M,S)の感度を、ここではガウス関数で近似して $$ S_{L}(\lambda) = \exp\left[ - \frac{(\lambda - 564)^2}{50^2} \right] $$ $$ S_{M}(\lambda) = \exp\left[ - \frac{(\lambda - 534)^2}{40^2} \right] $$ $$ S_{S}(\lambda) = \exp\left[ - \frac{(\lambda - 450)^2}{30^2} \right] $$ と表すことにしよう。 そして、それぞれの強度が(R,G,B)の値に対応すると解釈する(これは近似、あるいは仮定であって、厳密には正しくない)。

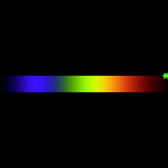
上は本物の虹の写真、下は亀場を使ったシミュレーション。
(主)虹は外側が赤になる。
シミュレーション(図下)では虹の左端は青で終わっているが、実際にはL,M細胞は波長の短い領域にも感度があるため、青の隣が紫に見える。
以下のひな形プログラムを参考に、亀場上に左図のような虹色の帯を描くプログラムを完成させなさい。
#include <math.h>
#include "turtle.h"
main()
{
float r,g,b,w ;
CON("localhost") ;
CLR() ;
FILL() ;
JUMP(-250,25) ;
EAST() ;
for (w=400 ; w<650 ; w=w+3) { /* 波長を400から650nmまで変化させる */
r = exp(-(w-564)*(w-564)/(50*50)) ; /* 赤の強度 */
g = exp(-(w-534)*(w-534)/(40*40)) ; /* 緑の強度 */
b = exp(-(w-450)*(w-450)/(30*30)) ; /* 青の強度 */
「見える色」を描画するプログラムを記述
}
}
|
 ヒント:
ヒント:
プログラム中に、指数関数を使っているので、コンパイル時に数学ライブラリのリンクをお忘れなく:
cc プログラム名.c -lm
3. 補色と色相環
補色の対応関係は色のモデルによって若干異なる。ここではRGBカラーモデルに基づいて説明を行なっている。
光の強度を0〜1で表し、ある色を表す三原色の配合を (r,g,b) と表すとき、(1-r, 1-g, 1-b)となるような配合は、どのような色を表すだろうか。 例えば、赤は(1,0,0)で表現されるが、これに対して、(0,1,1)は水色(青緑)となる。 このとき、赤と水色は、補色(complementary color)の関係にある、と呼ばれる。
その構成方法から想像されるように、補色の関係にある色は互いに使われていない色成分で構成されているため、対照的で、互いを目立たせる効果が高く、デザインなどに応用されている。 例えば、青緑色の地に赤で書かれた文字や記号は、とてもくっきりと識別することができる。
下図のように、色を円環状に並べ、180°反対側の、対向する色が補色の関係になるように描いた図を色相環と呼ぶ。

 練習:色相環の描画
練習:色相環の描画
タートルグラフィックスを使って、亀場に上図のような色相環を描かせなさい。
 ヒント
ヒント
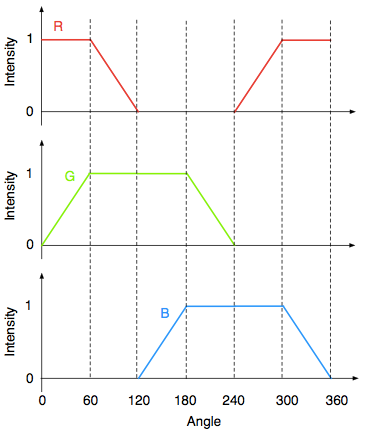
円環の周方向の角度と、(r,g,b)の配合割合の対応関係が下図のようになるようにプログラムすると良い。
右のグラフを見ると、例えば、60°の位置にある黄色(1,1,0)の補色は 60+180=240°の位置にある青(0,0,1)、であることがわかる。