情報基礎「Pythonプログラミング」（ステップ１・準備・アルゴリズム）

Pythonプログラミング（ステップ１・準備・アルゴリズム）

このステップの目標

アルゴリズムとプログラムの関係と対応を理解する。

1. アルゴリズムを考え、それをプログラムとして表現する

Pythonプログラミングと全く関係無さそうな話題かもしれないが、ここで『炊飯器でご飯を炊く手順』を考えてみよう。授業担当者の場合、ざっと以下のような感じになる：

Input: 精米済みの米 $n$ 合
Output: 炊きあがったご飯 $n$ 合
1: 容器に米を入れる
2: 水を入れ、米を撹拌する
3: 米が沈むまで待ち、上澄みの水を捨てる
4: 上澄みの水が大きく濁っている間は2:から繰り返す
5: 洗った米を炊飯器の容器に移す
6: 炊飯に容器内側の目盛り $n$ に達するまで水を入れる
7: 炊飯器をコンセントに接続する
8: 「炊飯」ボタンを押す
9: 「炊飯」ランプが消え、「保温」が点灯するまで待つ
10: 終了する

ご飯を炊いたことの無い人に「ご飯、3合炊いといてね」といったアバウトな指示は全く意味が無いように、コンピュータへの指示（コンピュータ・プログラム）も具体的かつ詳細に記述する必要がある。このように、問題解決に向けての一連の処理や作業の手順をステップに分解し、具体的に記述したものをアルゴリズム（algorithm）と呼ぶ。

炊飯器の中にもコンピュータが内蔵されており、エンジニアが炊飯のアルゴリズムを考え、それを（Pythonとは限らないが）プログラミングしているはずだ。

手順をどのくらい細かい手順にまで分解した上で、どのような語彙と文法を使ってアルゴリズムを記述する必要があるかは、もちろん、想定する機械（計算機）の機能によって変わる。もし完全自動式の未来型の炊飯器があったら、その機械のための炊飯アルゴリズムは、『白米をn合を炊く』の１行で済んでしまうかもしれない。一方、上に示したアルゴリズムは、現在普及している炊飯器を使い、人が作業することが暗に想定されている。

高度に抽象的なアルゴリズムを考えたとしても、それをPythonでコーディングする際には、より具体的で細かい手順に分解する必要が生じる。コンピューターを極限まで数学的に単純化したモデルがチューリングマシン(Turing machine) で、TMの機能だけでアルゴリズムを記述するのは恐ろしく面倒な作業になる。

であるから、アルゴリズムを考える際には、我々がどれくらい賢い（あるいはおバカな）計算機システムを相手にしているのかを、あらかじめ想定しておく必要がある。ここで我々が学ぼうとしているPython言語は、プログラミング言語の中では「高水準言語」に分類されているものの、あらかじめ備わっている機能はとても限られている（当然、「炊飯命令」などは無い）。

すると、きちんと手順（アルゴリズム）を記述するにはPython言語の語彙や文法を把握しておかねばならない一方で、Pythonでプログラミングするためには、まずアルゴリズムを考えなければならないことになって、これでは完全に循環論法である。良い例えではないかもしれないが、作曲の際には楽器の特性を考慮しながら楽譜を書かなければならない一方で、楽器を演奏するには楽譜が必要である。プログラミングの学習というのは、作曲法と演奏を同時に勉強するのとどこか似ているかもしれない。

その感じを掴んでおくために、具体的なPythonプログラミングに入る前に、Python言語（を含む一般的なプログラム言語）を使って問題解決の自動化を行う際、どれくらいの細かさでアルゴリズムを考える必要があるのか、トランプのカードを用いた簡単な例を使って、まずは頭の準備体操をしておきたい。

カードの並べ替え

以下では、データをトランプのカードに見立てて説明しているが、「コイン」や「麻雀牌の萬子や筒子」など、数値の大小が明確ならば、より親しみのあるモノに対応させて考えても一向に構わない。

テーブルにカードが２枚あって、それぞれ、aとbと書かれた枠内に置かれているとしよう。その他に、tと書かれた枠がもうひとつあるとする。そして、以下のルールに従ってカードを操作できるとしよう。

カードはちょうど１枚分の大きさの枠内にしか置けない
カードは１枚ずつ枠から枠に動かせる
カードの上に別のカードを重ねると、下側のカードは「消えて」しまう（あるいは、上のカードとひっついて、１枚になってしまう）。

このとき、aとbのカードの場所を入れ替える手順を、「コンピュータ・プログラミング流」に述べると、以下のようになる（右側に、実際に動作するPythonコードの例も示した）：

Algorithm:カードの交換	Pythonによるコーディング例(swap2.py)
Input: aとbに置かれたカード Output: 置き場所が入れ替わったカード 1: aにカード(例えば1)を置く 2: bにカード(例えば2)を置く 3: aをtに移動する 4: bをaに移動する 5: tをbに移動する 6: aのカードの数値を確かめる 7: bのカードの数値を確かめる 8: 終了する	a = 1 b = 2 t = a a = b b = t print("a=",a) print("b=",b)

Pythonには多重代入と呼ばれる機能があるので、a,b=b,a と書くだけで変数の入れ替えは可能。

上記のアルゴリズムを『aとbのカードを交換する』と一言で表しても、論理的に間違っているわけではないが、一般的なコンピュータのハードウェアには「二つのデータを１回の工程で交換する」という機能が備わっていないので、そのことを反映して、プログラミングの際に、データをひとつずつ移動するステップにまで分解して考えなければならないのだ。

　練習：5枚のカードの並べ替え

(左から)一列に並んだ置き場所a,b,c,d,e上にそれぞれ置かれた5枚のカードの順序を反転させるアルゴリズムを、2枚のカードの交換の例に倣って、記述しなさい。ただし、一箇所、仮置き場 t が用意されているとしなさい。

　解説:アルゴリズムの汎用化

あらゆる問題の規模に対応する

『カードの並べ替え』を考えるときに、2枚の場合、3枚の場合、... といった具合に、与えられたカードの枚数ごとに手順を考えるのは明らかにスマートではない。 $N$ 枚( $N$ は任意の自然数）のカードが並んでいる場合の手順を一般的に記述しておいて、枚数に応じて $N$ の値を「後から」設定できれば、はるかに融通が効く。

置き場所を番号や変数で指定する

カードの並べ替えの場合、どんな規模( $N$ の値)の問題にも対応できるようにアルゴリズムを記述するためには、カードの置き場所に a, b, c, ..という風に個別の名前を与えるやり方は破綻する（カードが1億枚あったら、1億通りの「地名」が必要になる）。そのような場合は、「何番目の置き場所」という風に通し番号をつけて管理するほうが理にかなっている。例えば、カードの置き場所全体に $a$ という名前をつけて、1億番目の置き場所は $a_{100000000}$ とするのがわかりやすい。さらに、置き場所の番号も、記号（変数）で指定できるようにして、 $a_{i}$ といった風に添え字を使った記法を導入すると、記述の幅がうんと広がる（ここで $i$ は場所を表す自然数）。例えば、 $a_{i}$ の右隣は $a_{i + 1}$ と指定できるし、左隣は $a_{i - 1}$ 、一番右端の置き場所は $a_{N}$ である。こうすれば、どんな $N$ でも対応できるはずだ。

反復動作の指示

置き場所 a, b にそれぞれカードが置かれている場合、すべてのカードを仮置き場 t に片付けるには、

1: a のカードを t に移動する
2: b のカードを t に移動する

と書けば事足りる。一方、 $N$ 枚のカードの場合、すべての置き場所についての移動を指示するには、上記の添字を使った記法を使って

$a_{i}$ $(i = 1, 2, \dots, N)$ のカードを、順次 $t$ に移動する

などと書きたくなる。ところが、 $\dots$ のところは、人間が正しく察してくれることを想定した記法である。つまり、添字の変化を表している $i = 1, 2, \dots,$ の箇所は、意地悪に解釈すると、例えば、1, 2, 3, 5, 8, ... の場合なども含んでしまう。こうした曖昧さを避けるには、起点、終点、そして「歩幅」まで、きちんと示しておく必要がある。この場合、アルゴリズムの記述は以下のようにすれば良い：

1: $i$ を 1 から $N$ まで 1 ずつ増やしながら 3: までを繰り返す:
2: 　　 $a_{i}$ のカードを $t$ に移動する
3: 繰り返しここまで

$a_{1}$ から順に $a_{2}, a_{3}, \dots$ と参照位置を変えながら、全てのカードを $t$ に移動させる

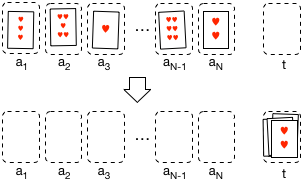
　練習：N枚のカードの並べ替え

一列に並んだ $N$ 個の置き場所 $a_{1}, a_{2}, \dots, a_{N}$ にそれぞれ1枚ずつ計 $N$ 枚のカードが置かれている。加えて、仮置き場 $t$ も使えるとする。 $N$ 枚のカードの順序を反転させるアルゴリズムを記述しなさい。

ここで、 $i$ 番目の置き場所 $a_{i}$ とし、「反復過程」を含め

Input: $a_{i}$ $(i = 1, 2, \dots, N)$ に置かれた $N$ 枚のカード
Output: 置き場所が入れ替わったカード
1: $i$ を ?? から ?? まで1ずつ増やしながら ?: までを繰り返す：
2: 　( $i$ の値に応じたカードの操作...)
3: 　...
4: 　...
?: 繰り返しここまで

の様式で記述すること。

「整列」については、参考書 p.30 例題2.25を参照

　練習：3枚のカードの整列

一列に並んだ置き場所（左から）a,b,c上に数値が書かれたカードが置かれている。カードの数値は全て異なるとしよう。最初のカードの配置にかかわらず、最終的にカードの数値が左から小さい順になるよう整列させるアルゴリズムを、「ヒント」の2枚のカードの交換の例に倣って、記述しなさい。

　ヒント

記述にあたり、二枚のカードの大きさを比較して、その大小に応じて、処理を切り替えることができるものとする。

例えば、カードが2枚の場合は

Input: aとbに置かれたカード
Output: 小さい順に並んだカード
1: a にカードを置く
2: b にカードを置く
3: a と b を較べ a >b ならば4:から実行
　　そうでなければ7:に移る
4: a を t に移動する
5: b を a に移動する
6: t を b に移動する
7: 終了する

あるいは、（この課題では記述量を減らすために）「交換」をひとつの操作として定義してしまって、

Input: aとbに置かれたカード
Output: 小さい順に並んだカード
1: a にカードを置く
2: b にカードを置く
3: a と b を較べ a > b ならば a と b を交換する
4: 終了する

と手短に書いてしまってもよいことにしよう。

発展問題として、参考書の例題2.25を参考に、 $N$ 枚のカードを昇順に整列するアルゴリズムを記述してみなさい。

　発展練習：カードの「山」の移動

ここまでは、「カードの上にカードは置けない（重ねたら、一番上のカードにまとまってしまう）」という状況設定を考えていた。以下の練習課題では、このルールを変更して

カードはちょうど１枚分の大きさの枠内にしか置けない
カードの上に別のカードを重ねることができる。ただし、カードに書かれた数値が下のカードより小さくなければならない。
カードは一番上のものを１枚ずつ枠から枠に動かせる

としてみよう。

三つの置き場所 a, b, cがあり、aに $N$ 枚のカードが積まれている。上記のルールに従い、カードに書かれた数値は、上から下に大きくなっている。カードを1枚ずつ移動させて、このカードの山を aからcに移動する手順（アルゴリズム）を見つけなさい。

カードの枚数が $N = 2$ のときをまず考え、 $N = 3, 4, 5$ と増やしてみなさい。

　ヒント

これは「ハノイの塔」という名前で良く知られている問題である。カードが $N$ 枚のとき、「山」を移動するには $N^{2} - 1$ 回の手数が必要なことがわかっている（2枚の場合は3回、3枚で7回, 4枚で15回）。

記述の際には、aからbへの移動を $a \to b$ と矢印で表すことにしよう（あるいは、 $b \leftarrow a$ 。Pythonの代入操作(=) との対応を考えると、こちらのほうが良いかもしれないが、いずれにしても、矢印の向きで移動方向が分かれば問題はない）。

　解説: 「関数」を使ったアルゴリズムの記述

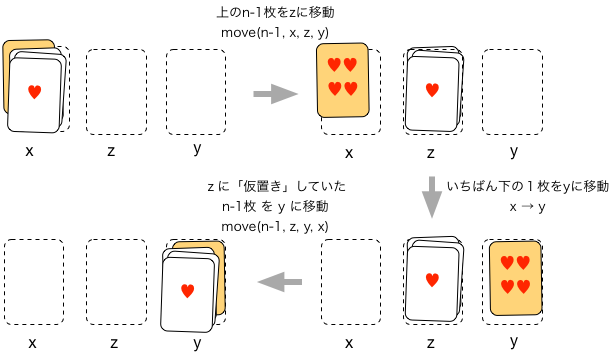
$x, y, z$ という3つの置き場所があったときに、 $x$ に積まれた $n$ 枚のカードを $y$ に移動する「行為」を $move (n, x, y, z)$ と記述してみよう。ここで、 $x, y, z$ は変数で、 $x$ の内容は置き場所aであったり、置き場所bであったり・・、と変わり得る、と考える。具体的には、例えば $n = 2$ のときは、

$move (2, x, y, z)$ の内容:
　　 $x \to z$
　　 $x \to y$
　　 $z \to y$

となるだろう。

$x$ に $n$ 枚の山があったときは、上側の $n - 1$ 枚をまず $z$ に移動し、一番下のカードを $y$ に移動後、 $z$ に積まれていた $n - 1$ 枚を $y$ に移せば良い。その手順は

$move (n, x, y, z)$ の内容:
　　 $move (n - 1, x, z, y)$
　　 $x \to y$
　　 $move (n - 1, z, y, x)$

と記述することができる（moveの中の $x, y, z$ の順序に注意）。

この、moveという「関数」を使うと、アルゴリズムは

Input: aに積まれた $n$ 枚のカード
Output: cに積まれた $n$ 枚のカード
1: 関数 $move (n, x, y, z)$ を定義する：
2: 　　もし $n = 2$ ならば
3: 　　　　 $x \to z$
4: 　　　　 $x \to y$
5: 　　　　 $z \to y$
6: 　　それ以外( $n > 2$ )なら
7: 　　　　 $move (n - 1, x, z, y)$
8: 　　　　 $x \to y$
9: 　　　　 $move (n - 1, z, y, x)$
10: 関数定義終わり
11:
12: 関数 $move (n, a, c, b)$ を評価する

のように表現することができる。このアルゴリズムをPythonに直訳したのが以下のコードである。

「ハノイの塔」のpythonコード例

hanoi.py

def move(n,x,y,z):
    if (n==2):
        print(x,"-->",z) ;
        print(x,"-->",y) ;
        print(z,"-->",y) ;
    else:
        move(n-1,x,z,y) ;
        print(x,"-->",y) ;
        move(n-1,z,y,x) ;

move(4,"a","c","b")

10枚のカードについて解く様子（YouTube動画）

コードを実行すると、4枚の場合の手順が画面に出力されるはずだ。プログラムの最後の辺りの"4"の値を変えれば、異なる枚数についても計算可能である。

この例では、「カードを移動する作業は・・・・をすることである」という風に、新しい語彙（ある種の動詞句）を定義することを通じてアルゴリズムが記述されている。このように、手順の記述方法には、いくつかの流儀があって、そうした流儀に適したプログラミング言語が（Python以外にも）沢山開発されている。