暦と日付の計算(基本編)
このページには、コンピュータを使って暦を計算する際の基礎事項をまとめておいた。
グレゴリオ歴
地球は太陽の周りを約365.2422日かけて一周している(1太陽年)。これを
$$ 365 + \frac{1}{4} - \frac{1}{100} + \frac{1}{400} = 365.2425$$
と近似しているのが、現在我々が用いているのはグレゴリオ歴である。 この方式の暦は1582年にローマ教皇グレゴリウス13世が制定したが、日本で採用されたのは、明治になってからである。
1年の日数に「小数点以下」はあり得ないので、1年の長さを1日単位で調整して帳尻を合わせなければならない。 上記の近似式からすぐわかる調整ルールは
- 4年に1回は1年を1日長く設定する
- 100年に1回は1日短くする
- 400年に1回は1日長くする
ということになるだろう。これに従えば、「平均的な」1年の長さは365.2425日になるはずだ。 そして、「$m$ 年に1回」の計算方法としては、「西暦年 $y$ が $m$ で割り切れたとき」と考えるのがいちばん自然だ。 そこで閏年を設けて、2月の末日がその調整日に充てられているわけである。
もちろん、上記は単なる近似にすぎないので、暦は地球の運行の状況から次第にずれてしまうが、追加の調整が必要になるのは、まだかなり先のことになりそうだ。 それに対して、地球の自転速度には多少揺らぎがあるので、ときおり「うるう秒」を設けて、1日の長さに微調整が加えられている。
 練習: 独自方式の暦
練習: 独自方式の暦
長期的に1年が平均的に365.2422日となるような、より簡単で精度もよい方式(閏年の設け方)を考案してみなさい。
 ヒント
ヒント
実数値を無駄の少ない有理数で近似する考え方として連分数展開が知られている。
うるう年の判定
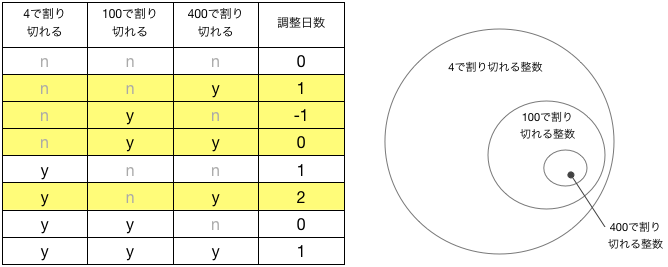
ある年 $y$ に何日だけ調整すればよいか、は、$y$ が 4, 100, 400 でそれぞれ割り切れるかどうか、で決まるので、 単純に考えれば、$2 \times 2 \times 2 = 8$通りの場合がありそうである。 それを表にまとめると、以下のようになる(表では、「割り切れる」を y、「割り切れない」を n と表記した):
ここで、黄色く示したのは「あり得ない」組み合わせであることに注意しよう。たとえば、400で割り切れるような数は、必ず 100 でも 4 でも割り切れる、等々。
そうすると、表の背景が白い箇所をみると、うるう年(調整日数が+1日であるような年)は、
4で割り切れ、かつ、100では割り切れない、かつ、400で割り切れない年 4で割り切れ、かつ、100で割り切れ、かつ、400で割り切れる年
の二通り、ということになることがわかる。
-1日や+2日の調整は不要で、たまの+1日分の調整だけで済むという点で、グレゴリオ暦というのは、何とも巧みにできているではないか。
「100で割り切れない数は400でも割り切れない」こと、加えて、「400で割り切れる数は、100でも4でも割り切れる」ことは自明なので、 上記のルールはさらに簡略化することができて、うるう年の判定は以下で十分である:
4で割り切れ、かつ、100では割り切れない年 または、400で割り切れる年
日数の計算
カレンダー上で離れた日付の間の日数を、時々知りたくなることがある。 例えば、あなたはあと何日生きられるかは分からないけれど、これまでに何日生きてきたかは知ることができる。 そんなとき、日付の計算は結構面倒なものだ。コンピュータにそれをやらせるにはどうしたら良いだろうか。
もともと、古代ローマのカレンダーは、春の農作業が始まる3月を1年の起点としていたらしい。 その名残は月の名称に残っており、Septemberの"sept"は7 (seven), Octoberの"oct"は8、Novemberの"novem"は9、 そしてDecemberの"dec"は10を、それぞれ意味している。
2月の長さはうるう年のルールによって変動するので、1年間を3月1日からはじめて、2月の末日をその年の最後、と考えると、年をまたいでの日数の計算が何かと楽になる。 3月を起点とすると、1年の各月の長さは
Mar Apr May Jun Jul Aug Sep Oct Nov Dec Jan Feb 31, 30, 31, 30, 31, 31, 30, 31, 30, 31, 31, 28 or 29
であり、それを累積すると
0, 31, 61, 92, 122, 153, 184, 214, 245, 275, 306, 337, 365 or 366
となる。ここで、翌年の1月はその年の13月、翌年の2月はその年の14月、と考えると都合が良い。
3月1日から $m$ 月1日までの累積日数(数列 0, 31, 61, 92, ..., 337)は不規則なパターンに見えるが、比較的簡単な数式、例えば、 $$ \left\lfloor \frac{153 m - 457}{5} \right\rfloor $$ で表すことができる。 ここで、見慣れない記号 $\lfloor \ \ \ \ \ \rfloor$ は、挟み込まれた式の値の小数点以下を切り捨てて整数値にする、という操作を表す。
実際に値を入れてみると、確かにこの式は3月1日から$m$月の最初の日までの日数を正しく与えている(ただし、$3 \le m \le 14$)。 例えば、$m=3$ とすると、3月1日から3月1日までの日数0となり、$m=4$ に対しては31, $m=5$ では61, $\cdots$といった具合である。
しかしながら、通常、こんな数式をすぐには思いつかないだろうから、コンピュータに計算させる場合は、関数として
def n_days_from_march_1st(m):
tab = [0, 31, 61, 92, 122, 153, 184, 214, 245, 275, 306, 337]
return tab[m-3] ;
と書いてもたいして効率に違いはないだろう。
次に、西暦0年3月1日から、西暦 $y$ 年2月末日までの日数を求めてみよう。 これは、案外単純である。 というのも、グレゴリオ歴の考え方から、$y$ 年の間に、4年に1回の+1日分の修正が $\lfloor y/4 \rfloor$ 回、 100年に1回の-1日分の修正が $\lfloor y/100 \rfloor$ 回、そして400年に1回の+1日分の修正が $\lfloor y/400 \rfloor$ 回入ることは明らかだからだ。 そうすると、1年の「基本日数」を365日として、求める日数は $$ 365 y + \lfloor y/4 \rfloor - \lfloor y/100 \rfloor + \lfloor y/400 \rfloor $$ となる。
では、ここまでの考察をまとめてみよう。
暦の原点を西暦0年3月1日とすると(その当時はまだグレゴリオ暦は採用されていなかったが、仮に、人類がずうっとグレゴリオ暦を使ってきたと仮定すると)、 西暦0年3月1日から、西暦$y$年$m$月$d$日までの日数は、 $$ 365 y + \lfloor y/4 \rfloor - \lfloor y/100 \rfloor + \lfloor y/400 \rfloor + \lfloor (153 m - 457)/5 \rfloor + (d-1) $$ となる。ただし、計算の上では、$m$が1, 2の場合は、その1年前の(すなわち$y \leftarrow y-1$とみなした上で)13, 14月、と見なす。
上式の最初の4項が、基点からその年の2月末日までの日数、 5項目が同じ年の3月1日からその月の初めまでの日数、そして最後の項がその月の初めからの日数に、それぞれ対応している。 日数のところを$(d-1)$としているのは、ここでは月のはじめを「0日目」と考えているためだ。
こうして、基点からの日数が計算できるようになったので、、例えば、二つの日付けの間隔(日数)を、基点からのそれぞれの日数の差として求めることができる。
「切り捨て」の計算
Pythonで、$\lfloor y/4 \rfloor$ を計算するには、yを整数とすれば、y//4と記述すればよい(//は整数の除算)。
ところが、もしy/4と書いてしまうと、Python 3の処理系はこれを実数の計算と見なしてしまう(つまり、結果は小数点以下を含む)ので注意が必要だ。
プログラムの先頭にimport math
を忘れずに書いておくこと。
計算結果が実数値となるような場合、その小数点以下を切り捨てた実数値を得るには、標準ライブラリ関数math.floor()を使えばよい。
参考までに、切り上げはmath.ceil()関数、絶対値はabs()関数である。
曜日の計算
ここで $x \mod m$ は $x$ を $m$ で割った余りを表す。
Pythonでは x%m と記述する。
1週間は必ず7日のサイクルで繰り返すので(「うるう曜日」は無いので)、曜日は、基準となる日付けからの日数を元にして求めることができる。例えば、 $$ \left( 365 y + \lfloor y/4 \rfloor - \lfloor y/100 \rfloor + \lfloor y/400 \rfloor + \lfloor (153 m - 457) / 5 \rfloor + (d-1) \right) \mod 7 $$ の値を調べれば、曜日が計算できるはずだ。このルールでは、0が水曜、1が木曜、... 6が火曜、に対応する。
ただ、この式はちょっと冗長な感じがする。 よく使われているのは、Zellerの式(Zeller's congruence)で、いくつかの異なるバージョンはあるものの、西暦$y$年$m$月$d$日の曜日は、 $$ \left( y + \lfloor y/4 \rfloor - \lfloor y/100 \rfloor + \lfloor y/400 \rfloor + \lfloor (13 m + 8)/5 \rfloor + d \right) \mod 7 $$
の値が0なら日曜、1なら月曜、・・・、6なら土曜日、と求められる。 ただし、これらの式では、前節で述べた流儀に従って、$m = 1,2$の場合は、上式で$y$を1減らし、かつ$m$を13,または14とおく。 つまり、1月と2月は、前年の13月と14月と考えよ、というわけである。