情報基礎A 「Cプログラミング」（ステップ７）

このステップの目標

配列変数を用い、配列要素への適正なアクセスに配慮したプログラムが書ける
やや複雑な問題でも、段階的に、データ表現とそれに対応したアルゴリズムの選択ができる

１．配列を使った処理

コンピュータを使って大量のデータを処理するために必須の機能のひとつ、それが配列だ。「プログラミングの入門編」といえども、この配列はマスターしておきたい。

　配列変数：沢山のメモリー（変数）を一括して確保し、通し番号でアクセスする

これまで書いてきたプログラムでは、変数（メモリー）が必要になったら、いちいちそれに名前を付けて、

int are ;
float kore ;

のように宣言していた。ところが、例えば、１０００人から成る集団があって、それぞれの情報（例えば体重）を使った処理をしたいような場合、同じような変数宣言を１０００回も書くのはごめんこうむりたい。このように、データの件数が多い場合（あるいは、データの件数が不定の場合）には、必要な個数のメモリを一括して宣言し、それぞれを通し番号（＊＊番目）で管理するのが理にかなっている。

Ｃ言語に限らず、一般のプログラミング言語では、こうした用途に使うために、配列型(array type)のデータ構造が用意されている。

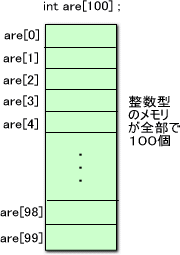
例えば、int型の変数を１００個、float型の変数を１０００個、一括して準備したい場合は、

int are[100] ;
float kore[1000] ;

のように宣言する。

配列変数へのアクセス

これらの変数の中身（データ）には、通し番号を付けて要素ごとにアクセスする。例えば、

are[3] = 17 ;

kore[ i ] = kore [ i-1 ] + kore [ i+1 ] ;

のように。つまり [ ] の中に、何番目のハコであるかを指定するわけだ。ハコの場所は、整数値で指定しても良いし、変数や数式であっても構わない。

配列へのアクセスの「はみ出し」は、コンパイル時には検出できないので、とても厄介だ。

ここで、気をつけなければならないのは、通し番号は０から始まることだ。１００個の要素から成る配列を宣言したら、おしまいの要素の番号は９９である（図参照）あらかじめ宣言した範囲を超えた要素（例えば kore[-1]やkore[100]）にアクセスすると、プログラムは「予期せぬ動作」をするので、十分注意すること。

配列データのコピー

配列変数の中身をそっくりコピーした場合、

int a[100],b[100] ;
・・・
a = b ;

のように書いてはいけない。「配列へのアクセスは要素ごとに行う」のがルールである。であるから、面倒だけれども、

int a[100],b[100] ;
int i ;
・・・
for (i=0; i<100; i=i+1) a[i] = b[i] ;

のように、反復処理を使って、要素毎に逐一代入する必要がある。

配列を使ったプログラムの例

所謂数値計算や、統計処理などを行う際に、あらかじめ配列にデータをセットしておいてから、あれこれ計算を進めるのが効率的である。以下は、配列中のデータから一番大きな値を探し出すプログラムの例。

例題８（ex8.c)

配列中のデータの中から最大値を探し出す。
これくらいのデータ件数では、プログラムで処理する有難味が薄いけれども、仮にデータが1000件ともなれば、最大値を見つけるだけでも人手で行うのは大変だろう。

#include <stdio.h>
main( )
{
  float x[10] = { 2.1, 5.3, 7.3, 4.7, 9.2, 1.2, 3.1, 5.3, 8.3, 4.8 } ;
  int i ;
  float maxval ;

  maxval = -100000 ;
  for (i=0 ; i<10 ; i=i+1) {
     if (x[i] > maxval) {
        maxval = x[i] ;
     }
  }
  printf ("最大値= %f\n",maxval) ;
}

プログラムの見所

配列変数の初期値を設定する場合に、いちいち、

x[0] = 2.1 ;
x[1] = 5.3 ;

配列変数の初期化

のように書くのは手間がかかるので、上記の例のように、まとめて

float x[10] = { 2.1, 5.3, 7.3, 4.7, 9.2, 1.2, 3.1, 5.3, 8.3, 4.8 } ;

のような書き方が許されている。ただし、この 配列={ }; の記法は、（プログラムの始まりの部分の）変数宣言でのみ使える。

配列データの中から最大値を探す手順

8行目から16行目にかけてが、配列の中から最大値を見つける処理。基本的な考え方は、すでにステップ６で説明してあるので、そちらを参照のこと。念のために、手順を言葉に「翻訳」すると以下のとおり：

   仮の最大値を、非常に小さい数値に設定しておく
   配列の中身を0番目から最後まで順に調べる：
   　　もし、i番目の値が、仮の最大値より大きければ、仮の最大値としてi番目の値をセットする
   この時点での、仮の最大値が、配列全体を通しての最大値

上の手順の一部をちょっとだけ変更すれば、最小値を見つけることもできる。

次に、もう少し複雑な処理の例として、配列中の数値の並び順を、小さい方から大きい方へ順に（昇順に）並べ変え、出力するプログラムを示す：

例題９(ex9.c)

配列データの整列（ソーティング）

#include <stdio.h>
main( )
{
  float x[10] = { 2.1, 5.3, 7.3, 4.7, 9.2, 1.2, 3.1, 5.3, 8.3, 4.8 } ;
  int i,j,n ;
  float w,median ;

  for (i=0 ; i<9 ; i=i+1) {
    for (j=i+1 ; j<10 ; j=j+1) {
      if (x[i]>x[j]) {
         w = x[i] ;
         x[i] = x[j] ;
         x[j] = w ;
      }
    }
  }
  
  for (i=0 ; i<9 ; i=i+1) {
     printf ("%f \n",x[i]) ;
  } 
}

プログラムの見所

ソーティングについての補足説明はこちら

プログラム８〜１６行目にかけてが、配列データの並べ変え（整列：ソーティング）を行っている部分。ソーティングの仕組みについては、機会を改めて学ぶことにして、ここでは、(i)変数（iとj)を使った配列変数の添え字のコントロール、 (ii)配列変数への（からの）変数の代入・配列変数を含む条件式の書き方、のふたつを、「ふむふむ」と眺めるだけに留めたい。

２．配列を使った統計計算

前のステップで行った統計計算プログラムを、配列を使ったバージョンに変更してみよう。先にまず、全データを配列変数に格納して、その後で、平均の計算を行っている。配列変数が登場する以外には、特に目新しい箇所は無いはずだ。

例題６A(ex6a.c)

#include <stdio.h>
#include <math.h>
main( )
{
  int n,i ;
  float x[100] ;
  float sum,average ;

  printf("データの件数を入れてください：") ;
  scanf("%d",&n) ;
  for (i=0 ; i<n ; i=i+1) {
    printf("%d 番目のデータ：", i+1) ;
    scanf("%f",&x[i]) ;
  }

  sum = 0 ;
  for (i=0 ; i<n ; i=i+1) {
    sum = sum + x[i] ;
  }
  printf("データの総和は %f です\n",sum) ;
  average = sum / n ;
  printf("平均値は %f です\n",average) ;
}

例題6Aの見所

配列の大きさは、データを入れるのに十分な数を用意しておく（例題では100）。
配列の要素は、０番目から始まる。それに対応して、ループ変数のiを0からn-1まで動かしている。
何番目のデータかを表示する際、「０番目」という表現は多少違和感があるので、i+1の値をプリントするようにしてある。

　練習：標準偏差の計算

例題６Aを発展させて，平均値だけでなく標準偏差も計算して，（両方を）表示するプログラムを書いてみなさい。

　ヒント

平均は，データをすべて合計して，それを件数で割ればよいから、式で表すと、データの件数を $n$ とすれば、 $$ \bar{x}=\frac{1}{n} \sum_{i=0}^{n-1} x_i $$ である。

標準偏差の計算手順

標準偏差は分散$V$の平方根で、「データのばらつきの程度」を示す重要な統計量である。分散は「平均値からの差を二乗した値の合計を求め，それを件数で割った量」である。式で書くと、平均を$\bar{x}$とすれば、分散は $$ V = \frac{1}{n} \sum_{i=0}^{n-1} \left( x_i - \bar{x}\right)^2 $$ で与えられる。これを使って、標準偏差は $$ s = \sqrt{V} $$ と計算できる。

けれども，分散は「二乗の平均値から　平均の二乗を引いた値」に等しいことを簡単に示せるので、具体的には，以下の手順で計算できる：

$x_i \; (i=0,1,2, \cdots , n-1)$を$i$番目のデータとする。データの件数は$n$とする。
データの総和$S$を計算する：\[ S= \sum_{i=0}^{n-1} x_i \]
二乗の総和$U$を計算する \[U = \sum_{i=0}^{n-1} \left( x_i \right)^2\]
平均 $E=\frac{S}{n}$ を求める
二乗の平均を $W = \frac{U}{n}$ によって求める
分散を $V = W - E^2$ で計算する
そうすると標準偏差は $s = \sqrt{V}$

２と３はforループを使って計算し（言うまでもなく、ステップ４で学んだ「総和のパターン」を使う。２と３をひとつのforループの中でまとめて計算してしまうのがスマート）、それらの総和の結果を使って$E$と$W$を求める。そして公式に従って標準偏差を算出する。

配列を使うと、添え字を伴う数式、例えばベクトルや行列などの計算を、自然な形で記述することができて、とても便利だ。この例では、数式の$x_i$と、配列のx[i]を対応させながらプログラムが書ける。ここで、添字の対応関係（具体的には、配列の添え字の範囲は0から始まり(要素数)-1までであること）には、くれぐれも注意すること。

平方根の計算には、これまでにも何度か登場した sqrt( ) を用いる。その際に、プログラム冒頭の#include <math.h>を忘れぬように。

　解説: 分散（標準偏差）の「推定値」

統計学の教科書には、$n$個のサンプル $\{x_0, x_1, \cdots, x_{n-1}\}$の分散（不偏分散）$\sigma^2$は、データの平均を$\bar{x}=\frac{1}{n} \sum_{i=0}^{n-1} x_i $として、 $$ \sigma^2 = \frac{1}{n-1} \sum_{i=0}^{n-1} \left( x_i - \bar{x}\right)^2 $$ であると書かれている。上の練習問題で用いた式と分母のところが1だけ違うが、どちらが正しいのだろうか。

平均$\mu$、分散$V$に従うような多量のデータの貯蔵庫があって、観測の都度、そこから$n$個ずつデータを取り出すというイメージ。

ここの箇所、統計学の教科書には $$ \frac{X_1 + \cdots + X_n}{n} \sim N(\mu, \sigma^2/n) $$ 等と表記されているかもしれない。

いま、対象としているデータの「真の」平均（母平均）が$\mu$、「真の」分散（母分散）を$V$としよう。そのとき、$n$個のデータを独立に何回も取得（サンプリング）して、その都度得られたデータの平均値（標本平均）と真の値とのずれの２乗平均を取ると $$ \left\langle \left( \frac{\sum_{i=0}^{n-1} x_i}{n} - \mu \right)^2 \right\rangle = \frac{V}{n} $$ が成り立つことが知られている。ここで$\langle \; \cdot \; \rangle$はサンプリングを繰り返して得た平均、を表す。つまり、観測した平均値は真の値の周りでばらついており、そのばらつきの程度は$V/n$である、というわけだ。

一方、データの分散は、「真の平均値$\mu$からのずれ」を使って、 $$ \frac{1}{n} \sum_{i=0}^{n-1} \left( x_i - \mu \right)^2 $$

全てのデータが等しい重みでサンプルされるとすれば、この関係はほとんど自明であろう。

で評価できる。そして、$n$の多少に関わらず、サンプル全体に渡るその平均は$V$に等しいはずである： $$ V = \left\langle \frac{1}{n} \sum_{i=0}^{n-1} \left( x_i - \mu \right)^2 \right\rangle $$

次に、上記の量$V$と、データの平均を使って求めた分散（標本分散）の期待値 $$ \tilde{V} = \left\langle \frac{1}{n} \sum_{i=0}^{n-1} \left( x_i - \frac{\sum_{i=0}^{n-1} x_i}{n} \right)^2 \right\rangle $$ との差を計算してみると、 $$ V - \tilde{V} = \left\langle \left( \frac{\sum_{i=0}^{n-1} x_i}{n} \right)^2 \right\rangle - 2 \mu \left\langle \frac{\sum_{i=0}^{n-1} x_i}{n} \right\rangle + \mu^2 $$ が得られる。ところが、上式の右辺は、「データの平均値と真の値とのずれの２乗平均」の左辺を展開した式に他ならないので、結局 $$ V - \tilde{V} = \frac{V}{n} $$ となる。知りたかったのは$V$であるから、この式を変形して、 $$ V = \frac{n}{n-1} \tilde{V} = \left\langle \frac{1}{n-1} \sum_{i=0}^{n-1} \left( x_i - \frac{\sum_{i=0}^{n-1} x_i}{n} \right)^2 \right\rangle $$

つまり、「分母を$n-1$」にして計算した分散は、その期待値が$V$に等しい、ということが分かった。

以上を定性的に再解釈すると

サンプルデータは、真の平均と比較して、より大きな値、あるいはより小さな値に偏っている可能性がある。その程度は、サンプル数 $n$ が少ないほど顕著である。
そうしたばらつきは本来分散に反映されなければならないが、例えば、値が「全体的に大きめ」であるようなサンプルに対しては、そのサンプルの平均 $\bar{x}$ も当然（真の平均より）大きめとなるので、$\bar{x}$ からの平均自乗距離（すなわち標本分散）は、真の平均 $\mu$ からの平均自乗距離よりも小さく見積もられてしまう。
そうした効果まで勘定に入れて「補正」すると、分母のところが $n$ ではなく $n-1$ となる。

というわけである。