情報基礎A 「Cプログラミング」（ステップ６）

このステップの目標

問題解決のアルゴリズムが与えられれば、前節までに学んだC言語の文法と機能を組み合わせ、プログラムに「翻訳」できる。
特に、統計計算や級数和などを、「総和」のバリエーションとして捉え、記述することができる。

1. Cによる統計処理の基礎

統計解析ソフト

文系・理系を問わず、実験や調査で得られたデータを分析する際に統計処理は欠かせない。件数の多いデータを処理したり、推定や検定などを行う際にコンピュータを活用するのは、今や常識と言える。統計計算には、所謂、統計解析ソフトを利用するケースもあるし（例えば、フリーソフトとしては R が有名)、 Excel等の表計算ソフトも、こうした用途に（も）よく使われる。

統計計算のかなりの部分は「総和」のパターン。

しかし、こうした出来合いのソフトは、中身がブラックボックスであるし、融通が効きにくい。このステップと次のステップにかけて，C言語を使った基本的な統計処理計算をいくつか紹介する。

平均値を計算するプログラム

例題６(ex6.c)

#include <stdio.h>
main( )
{
     int n,i ;
     float sum,data,average ;

     printf("データの件数を入れてください：") ;
     scanf("%d",&n) ;
     sum = 0 ;
     for (i=1 ; i<=n ; i=i+1) {
        printf("%d 番目のデータ：", i) ;
        scanf("%f",&data) ;
        sum = sum + data ;
     }
     printf("データの総和は %f です\n",sum) ;
     average = sum / n ;
     printf("平均値は %f です\n",average) ;
}

このプログラムを実行すると，最初にデータの件数を尋ねられるので，何か数値（例えば５）を入れる。すると，それぞれのデータの値の入力を求められる。データの入力が終わると，総和と平均値が表示される。

少々長く見えるが，これまでに学んだ事項（入出力、総和の計算、等）を組み合わせただけのプログラムだ。

　練習：最小値と最大値の計算

例題６を発展させて，平均値だけでなく、データ中の最大値と最小値も併せて表示するプログラムを書いてみなさい。

　ヒント

繰り返しの中で最大値を求めるためのおきまりのパターンは、以下のとおりである

最大値を見つけるパターン

   max = データ中のどれよりも確実に小さい数 ;
   for (何々) {
       if (データ > max) max = データ ;
   }
   この時点で、maxには、データ中の最大値がセットされている。

#include <float.h>
すると、float型で表現できる最大値（最大の絶対値）として FLT_MAXという記号を用いることができる。一方、FLT_MINはfloat型で表現可能な「最も0に近い（正の）数」。 double型の場合はDBL_MAX, DBL_MINを用いる。

整数については
#include <limits.h>
すると、最小値と最大値がINT_MIN, INT_MAXで参照できる。

原理は簡単で、変数maxには、「それまで」に見つかっが最大の値がセットされており、「現在」のデータがそれよりも大きかったら、maxにセットしなおす、という動作を繰り返せば、最終的にmaxの中には、いままでに登場した一番大きな数がセットされているはずである。「データ中のどれよりも確実に小さい数」には、（０ではなくて）例えば、-10000000などの（負の大きな）数を用いればよい。

敢えて書くまでも無いかもしれないが、反対に最小値を探すパターンは

   min = データ中のどれよりも確実に大きな数 ;
   for (何々) {
       if (データ < min) min = データ ;
   }
   この時点で、minには、データ中の最小値がセットされている。

ファイルに格納されたデータの利用

データの件数が多いと、数値をキーボードから入力するのは大変な手間となる。そんなときは、まず、エディタ（gedit)等で、

10
3.4 5.1 5.4 3.9 6.5 5.6 4.9 6.8 7.1 5.8

のようなデータファイルをあらかじめ作成しておいて(仮に、そのファイル名をsample.datとすると）、端末エミュレータで、コマンド

a.out < sample.dat

標準出入力
リダイレクション

を実行すると、ファイルの中身が自動的に「入力」される。ここで　< sample.dat　は、ファイル(sample.dat) の内容を（あたかもキーボードからタイプしたかのように）プログラムに「食べさせなさい」、という意味の指示である。このデータの例では、最初の10はデータの件数、その後、10個の数値が並んでいる。（この方法は、UNIXだけでなく、Windowsのコマンドプロンプトでも使うことができる。さらに詳しくは「標準入出力, リダイレクション」等のキーワードで検索すれば調べることができる。）

２．級数和の計算プログラム

「関数」を計算するプログラム（ ex7.c ）

三角関数や指数関数など，数学ではおなじみの関数は，もちろんプログラミングでもよく登場するので，sin(), exp( ) といった名前で簡単に数式中で使うことができる（例題５などを参照）。

けれども，こうした関数も，加減乗除の組み合わせだけで求めることができる。数学の教科書（解析学）を勉強すると、指数関数などの値は「テイラー展開」で求められることがわかるはずだ。例えば指数関数 e^x はこんな風に評価できる：

e^x = 1 + x + (1/2)*x*x + (1/6)*x*x*x + (1/24)*x*x*x*x ・・・・

これをもうすこし体裁よく書き直すと

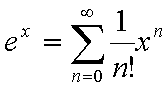
この式をよく見ると、係数の部分が1, 1/2, 1/6, 1/24という風に急激に小さくなっているので、先にすすめば進むほど各項の値も急激に小さくなっていくであろう（蛇足ながら０！は１である）。

だから、本当ならば（数学的には）足し算は無限回行わなければならないところだけれども、足し算を途中で打ち切っても結果はそれほど違わないはず。そもそも、コンピュータが扱える実数（float）には有限の精度しかないのだから。

この数式をCのプログラムで表すと，こんな風になるだろう（ex7.c）：

例題７ (ex7.c)

#include <stdio.h>
main()
{
  int n ;
  float sum, x, p, fact ;

  printf("ｘの値：") ;
  scanf("%f",&x) ;
  p=1 ;
  fact=1 ;
  sum = 0 ;
  for (n=0; n<10; n=n+1) {
    if (n>0) {
      fact = fact * n ;
      p = p * x ;
    }
    sum = sum + 1/fact * p ;
  }
  printf("EXP( %f ) = %f \n",x,sum) ;

}

変数factが階乗の部分を，pはｘⁿの部分をそれぞれ計算しながら，結果をどんどんとsumの中に足し合わせている様子がわかるだろうか。factとpの初期値を１にセットしてあるのに注意すること。　級数の和は，この場合，１０項目までで打ち切っている。

たとえば，xを１にしたら　e¹=2.71828・・・にちゃんとなるだろうか？

こちらのページにもう少し詳しい説明を書いたので参照のこと。

　計算の効率化を考える

上で述べたように，例えば，指数関数の計算は（C言語風に書くと）

e^x = 1 + x + (1/2)*x*x + (1/6)*x*x*x + (1/24)*x*x*x*x ・・・・

のような級数の和で求められる。同じ式を少しだけ変形すると

e^x = 1 + x*( 1 + (1/2)*x* (1 + (1/3)*x*(1 + (1/4)*x*(1 + ・・・・))))

のように，足したり・かけたり　の繰り返しでも表現できる。簡単のために最初の４項だけを考えると

e^x = 1 + 1*x*( 1 + (1/2)*x*(1 + (1/3)*x*(1 + (1/4)*x)))

ここで，かけ算の回数（つまり*の個数）を比較すると，変形前では９回だったのが，変形後は６回で済んでいる。級数をもっと「先」まで計算しようとすると，その差はどんどんと広がっていくだろう。このように，全く同じ計算をするにも，工夫次第で計算効率を改善できる場合が多い。そして、多くのソフトウェアは、こうしたぎりぎりのチューニングが施されている (腕に覚えのある者は、上記の手順で計算するプログラムを書いてみなさい)。

公式の選択も大切

例題７でx=1とおけば、ネピア数 e (=2.7182818...)を計算することができた。数学の教科書を見ると eの定義として

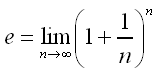
のように書いてあるから、こちらを使って（例題７とは異なるアルゴリズムで）計算したほうが簡単そうだ。そこで次のようにプログラムを作ってみた（ex7b.c）。

ex7b.c

#include <stdio.h>
main()
{
  int k,n ;
  float e ;
  printf("nの値(大きな数)：") ;
  scanf("%d",&n) ;
  e=1 ;
  for (k=0; k<n; k=k+1) {
     e = e * (1.0+1.0/n) ;
  }
  printf("e = %f \n",e) ;
}

nを大きくすればするほど、eの良い近似値が得られそうなものだが、実際はどうだろう・・・

　練習：正弦関数の計算

例題７を元にして，正弦関数を加減乗除の組み合わせによって計算するプログラムを作成しなさい。正弦関数は，以下のようなテイラー級数を使って計算できることが知られている。

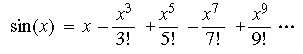
同じことだけれども，もう少し数式らしく書くと，こんな感じ：

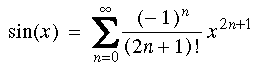
ポイント

「ｎ乗」や階乗の計算は，指数関数の場合と同様，ｎ回の掛け算によって求めるように工夫しなさい。
値が正しいか(あるいはどれくらい誤差があるか)、電卓などで検算してみること。xはもちろんラジアンで与えること。