情報基礎A 「Cプログラミング」（ステップ４）

このステップの目標

反復処理の流れと、変数の初期値、反復中の変化、終了の判定方法を的確に把握できる。
for文を使って、ループを含む基本的な処理を記述できる。特に、「総和」、および「条件が満たされるまで繰り返す」パターンを応用できる。

０．準備

反復処理のプログラムに間違いがあると、期待に反して「いつまで経ってもプログラムが終了しない」ことがある。ソフトが「固まった」状態だ。そんな状態から脱し、処理を強制的に中断するには、TurtleEditの中断ボタンを押すこと。

TurtleEditを使わず、Linuxのターミナル（端末エミュレーター）で作業している場合は、プログラム実行中にキーボードの下段にあるコントロール（Ctrl）キーを押したまま、アルファベットのｃ（コントロールC, CTRL-C）を押せば、プログラムは強制終了になる。

1. 反復処理

コンピュータは、プログラムに記述された膨大な手続きを、あっと言う間に処理できるから役に立つわけだが、その膨大な手続き（プログラム）のすべてのステップの全てを人間が書き下さなければならないとしたら、本末転倒だ。プログラムを記述する手間や時間のほうが、プログラムの実行時間を、はるかに上回ってしまうからだ。コンピュータが役に立つには、少ないプログラムの記述量で、膨大な処理ステップをこなすことができる、そんな仕掛けが不可欠なのだ。

そのために必要となるのが、繰り返し処理、あるいは反復処理だ。反復をマスターしなければ、プログラミングを学ぶ意味が無い。

数の足し上げプログラム

反復を伴う計算の例として、電卓を使った計算方法に倣って、1から10まで足し算を行うプログラムを書いてみよう。そうすると，きっとこんな感じのCのプログラムになるはずだ。

#include <stdio.h>
main( )
{
    int sum ;                                  電卓で計算すると・・・
    sum = 0 ;                                    MC
    sum = sum + 1 ;                              1 M+
    sum = sum + 2 ;                              2 M+
    sum = sum + 3 ;                              3 M+
    // 途中略
    sum = sum + 10 ;                             10 M+
    printf("１から１０までの合計： %d\n",sum) ;      MR 
}

最初に変数sumを0にセットしておいて，sum=sum+1; でsumに１がセットされ，次のsum=sum+2;で（sumには1がセットされているのだから）sumに３がセットされ・・・，という風にしていけば，正しい結果が得られそうだ。

C言語ではsum=sum+1; を縮めて、sum++; 書くことができる（ついでながら、sum=sum-1;なら sum--; ）が、ここでは、愚直な記法に徹したい。

sum = sum + 1 ; のような書き方（両辺に同じ変数が現れる）は「定型文」として頭に入れておきたい。「現在のsumの値に１を加えた値を，あらためてsumにセットする」わけだから，この計算をおこなうと，sumの値は１だけ増えることになる。

上記のプログラムで, 「sum = sum + （数値）」の（数値）のところが１，２，３・・・１０のように規則的に変化していることに気づいてほしい。

ここで、新たに変数ｎを使って上のプログラムを

#include <stdio.h>
main( )
{
    int n,sum ;      
    sum = 0 ;  
    n=1 ;
    sum = sum + n ;  
    n=n+1 ;
    sum = sum + n ;
    n=n+1 ;
    sum = sum + n ; 
    // 途中略
    sum = sum + n ; 
    printf("１から１０までの合計： %d\n",sum) ;
}

と書き直してみたらどうだろう。そうすると，「 sum = sum + n ; n=n+1 ; 」をちょうど10回繰り返す構造になっているのが分かる。この計算をC言語流に表現したのが，次の例題４aだ。

例題4a (ex4a.c)

#include <stdio.h>
main( )
{
     int n, sum ;
     sum=0 ;
     for (n=1 ; n<=10 ; n=n+1) {
        sum = sum + n ;
     }
     printf("１から１０までの合計： %d\n",sum) ;
}

まずは動作を確認するため、このプログラム(ex4a.c）をコンパイルして、実行してみよう。

　for文による反復処理の記述

for文

C言語には，「反復」を表現するためのいくつかの方法が用意されているが、その中でも最もよく使われる、for文を使った方法をここで学ぶことにする。 for文は、これまで登場したCの文よりも、いささか複雑な構造をしており、４つのパートで構成される。

反復の前に一度だけ実行される文
1回分の反復の度に行う処理
繰り返しの継続条件
繰り返す内容

そして、これらを次のように配置する：

for( 反復の前に一度だけ実行する文 ; 繰り返しの継続条件 ; 反復の都度実行する文) {

    繰り返す内容 ;
    
}

ここで、for文の丸括弧の中のセミコロンは各パーツの区切りを示すために必ず必要。また、「繰り返す内容」の箇所には、（if文の場合と同様に）、｛文１;文２;文３;・・・;｝　のように「やりたいこと」を列挙する。

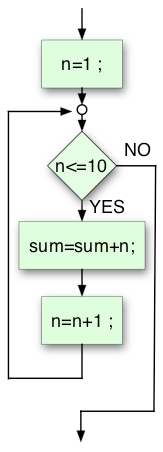
例題4aのforループの部分を流れ図にしたのが左図である。基本形との対応関係は：
　反復の前に一度だけ実行される文：n=1 ;
　繰り返しの継続条件： n<=10
　1回分の反復の度に行う処理： n=n+1 ;
　繰り返す内容： { sum=sum+n ; }
図から、プログラムの流れがループ構造になっている様子がわかる。

ここで大切なのは、for文のパターンに従って、文法的に正しく記述できるだけでなく、処理の各ステップで各変数の値がどのように変化してゆくのかをきちんと頭の中でシミュレーションができるようになることだ。その例を別ページに示したので、参照のこと。

　練習：奇数の和と階乗の計算

例題4aをひな形にして、

１から１００までの奇数のみの合計($1+3+5+\cdots+99$)を計算するプログラムを作成せよ。
１から１０をかけ合わせた結果（１０の階乗:$10!=1 \times 2 \times \cdots 10$）計算するプログラムを作成せよ。

　ヒント

奇数だけの合計を求めるには、(1)forループの変数ｎを１から始めて２ずつ増やすようにするか，(2) forのところはそのままで，ループの中でｎの値をチェックしながら，ｎが奇数の時だけsumに加える、ふたつのやり方がありそうだ。後者を採用した場合，整数 n が奇数かどうかを判断するには、if文を使って、

if ( n%2 != 0 ) { ・・・}　

という書き方を使えばよい。n%2は「ｎを２で割った余り」。であるから、このif文は「ｎの値を２で割った余りが0に等しくない場合は・・・を実行せよ」ということになる。

別のアプローチとして、$k$を整数とすると$2 k + 1$は奇数となるから、$2 k +1$が100以下となるように0から始めて$k$を1つずつ増やしていく、というやり方も考えられる。

　練習：閏年の一覧表示

２０００年から２１００年の間の閏年のリストを表示するプログラムを、以下の雛形から出発して、作成してみなさい。閏年かどうかの判定方法はひとつ前のステップを参照のこと。

#include <stdio.h>
main( )
{
  int year ;
  for (year=?? ; ?? ; ??) {
    if ( ???????? ) {
       printf("%d\n",year) ;
    }
  }
}

2. for文を使いこなす

　forを使った「定型文」

Cの構文の中ではおそらくfor文がいちばん複雑ではないかと思う。けれども、いくつかの典型的なパターンに従って使う場合がほとんどなので、それらをしっかりと押さえておけば、大抵の問題に対処できるだろう。

カウントダウン
実数のループ変数
総和の計算
無限ループ

書き方のパターン	コメント
for (i= から ; i <= まで ; i=i + ずつ) { 反復内容 }	上の例でもたびたび登場したパターン(iは整数型と想定）。 i=0からn回反復する場合は、for(i=0; i<=n-1; n=n+1)となる。もちろん for(i=0; i<n; n=n+1)でも同じ。
for (i= から ; i >= まで ; i=i - ずつ) { 反復内容 }	「から」に大きな数を入れて、そこから「カウントダウン」させるには、「・・・ずつ」の箇所を引き算にすればよい。反復の継続条件を表す不等式の向きが逆になることにも注意。
float x ; for (x= から ; x < を超えないで ; x=x + ずつ) { 反復内容 }	実数をあるステップで「刻みながら」反復する場合継続条件の等号に用心。x = x + dx ; をN回繰り返した結果が、誤差のために、x + N*dx に等しくなるとは限らないからだ。
s=0 ; for (n= から ; n <= まで ; n=n+1) { n番目の値の計算・・・; s = s + n番目の値 ; }	総和 $$ S = \sum_{n=\cdots}^{\cdots} s_n $$ を計算する場合は、いつもこのパターン。総和を入れるための変数（左ではs）の初期化も忘れぬように。
for (;;) { ・・・ ; if (条件) break ; ・・・ ; }	for文の「3点セット」の箇所を空にすると、これは「無限ループ」を表す。文字通り、いつまで経っても繰り返しつづけるプログラムだ。プログラムはいつかは終了しないと困るので、反復内容の中にif文を置いて、そこでループを終了させることができる。break;文が実行されると、ただちにループを終了して、次のステップ（for文の次）に処理が移行する。

同じ結果を得るためのプログラムの書き方は何通りもある。例題4aのプログラムを上記の「無限ループ」の定型を使って書き直すと、以下のようになる。 for文のパーツを(;;)の中から取り出したような格好だ。

例題4aの別バージョン。
例題4aでは、「繰り返しを継続する条件」であった箇所が「繰り返しを停止する条件」に変わっている（つまり不等号の向きが逆転している）点に注意。

#include <stdio.h>
main( )
{
     int n, sum ;
     sum = 0 ;
     n = 1 ;
     for (;;) {
        if (n>10) break ;
        sum = sum + n ;
        n = n + 1 ;
     }
     printf("１から１０までの合計： %d\n",sum) ;
}

「総和」の定型のための練習課題

　練習：ゼータ関数の値の評価

リーマンのゼータ関数(Riemann zeta function) $$ \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} $$ は、数学の問題の各所に関係した大変に興味深い対象である。例えば、$\zeta(2)$の値は、以下のように、円周率と関係のあることがわかっている： $$ \zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6} $$

C言語の「総和の計算」のパターンに、ゼータ関数を当てはめることで、ζ(2)の値を数値的に評価してみなさい。

　ヒント

注：N項目から無限大項目までの「足し残し分」の見積もりとして
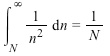
c-4-eq-zeta2-remaining
と考えると、N項目で和を打ち切った場合に想定される誤差を（ある程度）予想できるだろう。

#include <math.h>しておくと、M_PIという記号に円周率がセットされる。

数値計算で無限回の総和を計算することはできない。そこで、どこか大きなnで（例えば1000で）総和計算を打ち切らざるを得ない(左の注も参照)。

総和の各項である 1/(n*n)は、整数として計算すると、0になってしまう。それを避けるには、1.0/(n*n) と記述すればよい。

#include <stdio.h>
#include <math.h>
main( )
{
  int n ;
  float s,zeta2 ;
  s=???
  for (n=?? ; ?? ; ??) {
     ?????? ;
  }
  
  zeta2 = M_PI * M_PI / 6.0 ;
  
  printf("総和によって求めた zeta(2)= %f\n",s) ;
  printf("数学的な結果 =%f\n",zeta2) ;  
}

　条件が満たされるまで反復するプログラム

以下は、黄金比(Golden ratio)と呼ばれる「有理数から最も遠い無理数」( $\phi = (1+\sqrt{5})/2 = 1.618033988\cdots$)を連分数表示したものである。

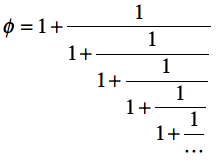
$c-4-eq-cont-frac-golden-ratio$

この連分数を、定義に従って「そのまま」数値計算してみよう。計算にあたっては、「下」から攻めてみるのが良さそうだ。$k$ステップ目の計算値を$\phi_k$とすると、次のステップの値は $$ \phi_{k+1} \leftarrow 1 + \frac{1}{\phi_k} $$ となるはず（下図参照）。

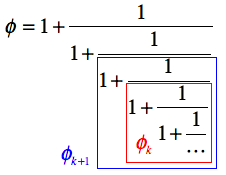
$c-4-eq-cont-frac-golden-ratio-2$

そうすると、この計算を繰り返すことで値が評価できそうだ。このように、「現在の値」を使って「次の値」を計算する、という手順の繰り返しは、反復処理の典型的なパターンだ。

ここで、$\phi_k$を変数 a、$\phi_{k+1}$を変数 b に対応づけて、もう少し具体的にアルゴリズムをまとめたのが以下である：

初期値（式の$\cdots$のところの値）が分からないのに果たして計算がうまくできるのか心配になるけれども、「適当な」値から出発しても、最終的には正しい値に収束する。

aに初期値を設定
以下を反復
   b=1+1/a
   もし|a-b|が十分小さければループを抜ける
   a=b
反復ここまで
aの値をプリント

さらにこれを「無限ループ」の定型に当てはめて、Cのプログラムに翻訳すると以下のように書ける。プログラム中で、ループを何回繰り返すかは陽には指定されておらず、「前」の値と「後」の値の差が十分小さくなったところで繰り返しを抜けるように書かれている。

例題4b (ex4b.c)

連分数を使って黄金比を計算するプログラム例

fabs( )は絶対値を返すCの関数

#include <stdio.h>
#include <math.h>
main()
{
    float a,b ;
    a=1.0 ;
    for (;;) {
        b = 1+1/a ;
        if (fabs(a-b)<0.0001) break ;
        a = b ;
    }
    printf("計算結果= %f\n",a) ;
    printf("数学的な結果= %f\n",(1.0+sqrt(5.0))/2.0) ;
}

「条件が満たされるまではずっと反復」の定型のための練習課題

　練習：連分数の計算

黄金比のプログラム例を参考に、$\sqrt{2}$または$\sqrt{3}$の値を以下の連分数を使って評価するプログラムを作成しなさい。

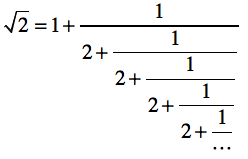
$c-4-eq-cont-frac-sqrt2.$
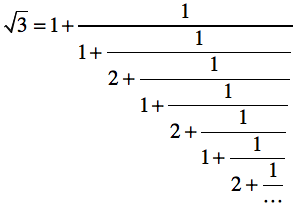
$c-4-eq-cont-frac-sqrt3$

　ヒント

繰り返しの「単位」を上手に見極めること。いずれも「最後の１回分」だけ、式のパターンが異なる点に注意。

亀場で練習：正多角形の描画

タートルグラフィックスのページの前半部分をよく読み、反復処理を用いて、半径100の円に内接する大きさの正7角形を描画するプログラムを作成しなさい（ただし、円は描かなくてよい）。