かなり荒っぽい実験であっても非常によい統計性が得られ, しかも結果が物質に依らないことは, 一見複雑に思える衝撃破壊が比較的単純で一般性のある シナリオで進行していると思わせるに十分である. 一般的に言って,生成される破片の性質は壊される前に物体に 仕組まれていた性質を反映している可能性もあるし, あるいは衝撃による歪みの伝搬や壊れ方等のダイナミクスに何か 特徴があるのかもしれない. ここではまず,二つの比較的単純な確率的破壊のシナリオと その結果生じる破片の分布から考察してみよう.
まず,今世紀半ばにコルゴモロフが提案したシナリオを考えよう[9]. 物体になんらかの衝撃力が加わると,大きな歪みを生じた箇所が まず壊れるであろう. その時,その位置はランダムであると仮定する. 強い歪みが継続すれば,第一段階で生成された断片の中でも同様な 破壊が繰り返し進行し,やがて小さな破片の集合が生成されるであろう (図(a)参照). 簡単のため一次元系を考えると,この結果生じる破片のサイズ(長さ)分布は 対数正規分布となることが中心極限定理を使って示すことができる. Ishiiらは金属管中に長いガラスロッドを入れ,高所から硬い 床に落下させる実験を行い,回収したガラス片の質量分布を調べた[10]. この実験では,落下による衝突でガラスロッドが幾度にもわたり 繰り返しへし折られると考えられ,状況はコルモゴロフのシナリオに近い. 事実,比較的大きいサイズの破片については,対数正規分布が実験結果を良く 再現すると報告されている.
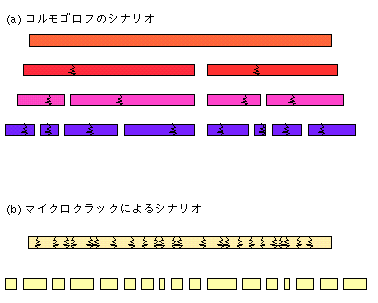
二つ目のシナリオは,マイクロクラックのランダムな活性化である[11]. どのような物質でも,その内部には無数の欠陥が存在し,物質の強度 はそうしたマイクロクラックに大きく左右される. 事実,マイクロクラックを考慮せずに原子間の結合力のみから 物質の強度を見積もると,現実の物質と比較して遥かに大きな値になって しまうと言われている. こうしたマイクロクラックがあらかじめ一様に物質内に分布 すると仮定しよう. 衝撃を契機にしてこれらの小さな亀裂がランダムに活性化し, 大きな亀裂に発展し破壊に至る様なプロセスを考えると, ある長さの中で活性化される亀裂数は ポアソン分布に従うため,結局サイズ(長さ)分布は指数分布となる(図(b)参照). 指数関数型の分布関数は,金属等に急激な負荷を一様に加える実験等で 実際に見られている. 例えばMottらが提案した分布関数 n(m) 〜 exp(- c m1/d) (Mott分布)は岩石や金属を粉砕する実験の結果をよく再現する. このシナリオが成立するためには,マイクロクラック分布の一様性 だけでなく,負荷も一様に加えられるという条件が必要である.
いずれにせよ,こうした全くランダムな破壊プロセスは衝撃破壊の モデルとしては単純すぎる様に思えるし,我々が期待するようなべき乗則 も見いだし難い. では,衝撃破壊はどのようなプロセスを経て進行するのであろうか? 衝撃破壊は三次元的でしかも音速程度で進行する高速な現象である ため,実験的にその詳細を捕らえることは容易ではないが, 高速度撮影装置などを駆使してその動的過程を直接測定する試みが 行われている. ガラスを使った実験によると,加えられた衝撃により発生した 歪みは圧縮波として試料を進行するが,それより遅れて 亀裂発生が局在する領域が平面波的にほぼ等速度で進行する様子 が観察されている[12]. こうした領域は "failure wave" と呼ばれており,failure wave の通過後に破片が飛散し始める様子が捕らえられている. こうした failure waveは,衝突破壊のみならず爆破に際しても観察されている. こうした知見から,音速程度の速いダイナミクスが重要らしいこと, 亀裂生成は物体内で一様に生じるのではなく「破壊面」とでも呼べる 面上に局在すること,が理解の鍵になると思われる.