
高速度カメラの撮影などによって破壊進行の素描は得られるものの, 実験的な制約を越えた理想系に近い実験としてのコンピュータシミュレー ションは非常に有力な研究手法であることは言うまでもない. ここでは高速破壊の数値シミュレーションの例として,最近筆者が 行った簡単なバネモデルによるモデリングとその計算例を紹介しよう.
まず壊されるべき物体を以下のような簡単なモデルで記述してみる. まず考慮せねばならないのは,物体の慣性と弾性である. 単純な固体の描像としてよく使われ,数値シミュレーションも容易な 「バネモデル」をここでは採用してみよう. 質量mの質点が三次元立方格子状に配置されており, それぞれ六つある最近接と第二最近接どうしの質点がバネで結ばれている. モデルはなるべく単純な方がよいが,第二近接を結ぶ「斜めバネ」は 三次元弾性を再現するためには必須であり,もしこれがないと 筋交いのない日本家屋のように剪断応力に対して(線形)弾性が生じない. 現実の物体は,高速な変形に対してある程度のエネルギー散逸が 伴うと考えられるため,ここでは各バネにダッシュポットを付加し, 相対速度に比例した抵抗力が発生すると仮定した.
ここで,以下の破壊の条件を導入する. 「もしある時刻でのバネの伸びδが,限界的な長さδc を越えたら,そのバネを切断する.一度切れたバネは,二度ともとには戻らない.」 これに従うと,物体が割れた後には割れ目同士は互いに影響を及ぼさない. また,破片同士が出会っても衝突せずにすり抜けることになる. これは一見非現実的に思えるが,実は破片生成に関しては本質的ではない.
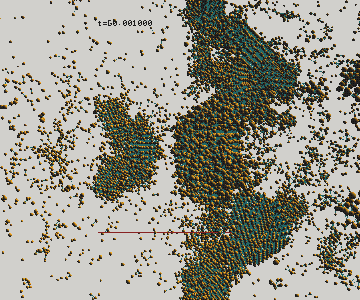
初期条件として,大きな変位ないし速度をモデル結晶の表面に加え, それぞれの質点をニュートンの運動方程式に従って時間発展させると, 内部に歪みが伝搬し, 破壊条件を満たすバネは非可逆的に切れる. 図は33×33個の質点からなる立方体の, 向かって左側の面に瞬間的に力を加えて破壊させた例である. こうした一連の過程は,初期条件として与える若干のランダムネスを 除けば全く決定論的に進行するが,結果として得られる破片の対称性は低い. チョークをへし折った場合のように,進行する亀裂には不安定性が 内在するため,決定論的な破壊のルールであっても結果は十分に複雑になり得る のである.


衝撃による破壊の進行をシミュレーションで観察すると,実験からは 得にくいであろう情報も容易に解析できる. この系ではモデル結晶内にはマイクロクラックは仕組まれていないため, 新たな亀裂の生成によって破壊は進行する. 亀裂が生成される位置は,ごく薄い層を成して面状に局在し,それが結晶の 縦波の音速程度で走り抜ける. これは前節の failure wave に相当すると思われる. モデル結晶にインパクトが与えられてから粉々に砕けるまでの間は, おおまかに言って幾つかの特徴的な段階に分けられる. (i) 試料の表面にインパルス的負荷が与えられ,破壊が開始されるまで, (ii) 亀裂の生成面が音速程度で試料内を移動し,試料の他端に到達する間, (iii) 破片が飛散する最終的な段階. 最終的に切れるバネの総数のうち,その大部分は(ii)の段階で既に切れてしまう. つまり,物体の各所はヒビだらけの状態になっている. 段階(iii)では,亀裂の入った物体が,僅かに残った接合点を引きちぎり ながら飛散する. 数値的にエネルギー収支を調べると,衝撃によって得たエネルギーのうち 殆ど(95%以上)は生成された破片の運動エネルギーに転化している.
破片同士の二次衝突過程が一切考慮されていないなど, かなり単純化されたモデルによるシミュレーションではあるが,これらは 実験的な知見をよく再現している. しかも,破片の累積質量分布を調べると,最終的にべき乗関数の裾がはっきり と現れ,べき指数は2/3に非常に近い値を取る.