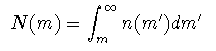 (1)
(1)
破壊という言葉にはどうしても否定的な響きあり, 秩序や対称性を重んずる科学の対象としてはどこか縁遠い. その一方で,そのメカニズムの理解は工学はもとより惑星科学や 地球科学における大きな関心事であった. 宇宙に無数に漂っているであろう小惑星にまず注目してみよう. 小惑星は年々沢山の数が発見されており,現在は6000個程度が知られている. それらの多くは火星と木星の間の軌道にあり,有名な小惑星帯 (アステロイドベルト)を形成する. 小惑星はかつてその母天体の破壊によって形成されたと考えられており, その意味ではまさに星屑といえる. 破壊の原因としては,木星の潮汐力,天体同士の衝突などが考えられているが, ここでは衝突生成仮説の立場を取ろう.
これまでに直径が100km以上の小惑星はその99%以上がすでに 発見済みであると考えられているが,小さなサイズのものについての 知識は必ずしも十分ではない. ただし,小惑星全体の質量の総和は意外と小さく,地球の月程度以下 であろうと考えられている. 小惑星は表面の反射能(アルベド)や組成によっていくつかの グループに分けられており, こうした性質の差異は,おそらくはそれが由来する母天体そのもの,あるいは 母天体内で断片が生じた位置に由来すると考えられる. また,軌道にもいくつかの顕著な特徴を持つグループが存在する[1].
さて,個々の小惑星ではなくて,小惑星の集合には何か特徴はありはしないか? こうした物体の集合を特徴付けるには,その累積質量分布関数を調べるのが 有用である場合が多い. まず,破片を質量の大きい順に並べ換え,大きい順に1から番号をふる. 質量を横軸に,その番号を縦軸にプロットすれば累積質量分布が得られる. 質量分布関数 n(m) を使うと累積分布 N(m) は
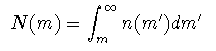 (1)
(1)
各種観測によって知られている小惑星の累積質量分布をグループ毎に とると,それらがべき乗関数
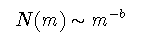 (2)
(2)
累積質量分布がべき乗関数になる場合には,累積サイズ分布関数もべき乗関数 N(s) ∝ s-b'となる. ここで言うサイズは,小惑星の径を考えればよい. 一様な物体を仮定すると, 累積質量分布の指数を$b$と累積サイズ分布の指数を b' の間には b = b'/d なる関係があることは簡単に示せる. 実際の観測結果の解析には,サイズ分布が使われることも多い.
月などの衛星や惑星の表面に見られるクレータは隕石の衝突によって 生じたと考えられており,その成り立ちは衝突した隕石の 特徴を反映しているはずである. それらのクレーターのサイズは月面に衝突した隕石のサイズのみに依存する わけではないだろうが,隕石のサイズとクレーターのサイズとの 間には強い正の相関があると考えるのが自然である. 望遠鏡で月面のクレータを観察すると,大きなクレータは 比較的少ないのにたいして,小さなクレーターは無数に存在するように 見える. 事実,小惑星の分布を調べるのと同様な方法でクレータのサイズ(径)について 分布を調べてみると,実際にその分布形は見事なべき乗則に従って いるのである [4]. また,月面の岩石を詳しく調べると,数ミクロン程度以下のマイクロクレータ が見られ,これらのサイズもべき乗関数でよく表現される. このことは,大きな隕石のみならず,宇宙を漂う微粒子もまたべき乗的な サイズ分布であることを示唆しており興味深い[5]. さらには,月面上の礫そのもののサイズ分布がべき乗則に従うという報告 もあり,累積質量分布に換算すると,b=2/3 を支持するデータが 得られている[6].
さて,地上に目を転じよう. 小惑星やクレーター形成の模擬実験として ガラスや岩石などの脆性体を衝撃破壊する実験報告はこれまでに多数ある. それらは宇宙での現象の再現としてももちろん興味深いが, コップを床に落とした時にどう割れるか,といった日常的な問題でもある. 衝突破壊実験は,岩石や氷,ガラスなどの標本に高速の物体を衝突させる, あるいは標本を硬い壁に衝突させる方法で行われ,その際に標本全体が飛散 しないようゲルなどで覆って生成された破片の回収率の向上が図られる場合もある. こうして得られる破片の累積質量分布は,多くの場合にべき乗的であって, 実験によりかなりのばらつきはあるものの,指数 b が小惑星と同じく 2/3 に近い値を取る報告例が多い.
ここでは,最近デンマークのOddershedeらが行った興味深い実験を紹介しよう [7]. 彼らは,試料となる物質の種類,および物体の形状を様々に変えて 衝突破壊の実験を行い,その分布を調べた. 試料を固い床の上に落とすだけの非常に簡単な実験ではあるが,得られる 質量分布が非常に奇麗なべき乗形を示す. 試料として一週間程度固めた石膏を使い,立方体ないし球に近い形状の試料 については b = 2/3 に非常に近い値を得ている. さらに,ジャガイモ(皮は剥いてある!),石けん,パラフィンを凍結させた試料 についても同様の実験をし,結果が物質に依存しないことを確かめた. ところが,指数は試料の全体的な形状には依存性を示し, 辺の長さが A, B, C であるような直方体の落下実験で得られる指数は
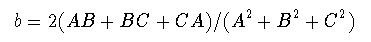 (3)
(3)
ところがその後,デンマークの他のグループが同様の実験を行い, 指数は(3)式で与えられるように物体の形状に関して連続に変化するのでは なく,試料の次元性のみに依存すると主張した[8]. すなわち,アスペクト比の大きな試料を使うと,累積分布関数に 折れ曲がりが見られ,異なる分布形のクロスオーバーが見られる. つまり,指数が一見連続的に変化するのは,分布関数のオーバーオールな 勾配を測定したことによる可能性が高い. このことはまた,指数が試料の次元性のみに依存するという,ある種の ユニバーサリティを持つ可能性をも示唆している.