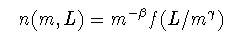 (4)
(4)
では,べき乗的な質量分布はどのようにして生じるのであろうか? 十分に大きい試料の一端に衝撃を加えて破壊実験を行った場合, これまで述べた知見から,破壊面は音速程度で試料内を進行し, それが通過した部分では骨格となる亀裂がすでに出来上がってしまうと考えられる. そこで,破壊を破壊面上で発生した亀裂による物体の分割過程としてとらえよう. Inaokaらはこうした点に着目し,三次元衝撃破壊を擬二次元 + 一次元 系に単純化したモデルを考案し,シミュレーションによって奇麗なべき乗分布 を得ており,さらに安定分布の議論からべき指数b=2/3を導出している. これは,亀裂の浸透(パーコレーション)とも言える視点である. パーコレーションの問題では,サイトやボンドの占有確率をある臨界値 にとると,連結クラスターのサイズ分布がべき乗分布に従うことが知られている. ところが衝突破壊においては,占有確率に相当するパラメータは 外部から制御されているわけではなく,むしろ 系が自らを臨界的な状態に調整した結果べき乗分布が達成されてされている (自己組織臨界現象)と見ることもできる. しかしながら,そのメカニズムについてはまだ十分に明らかにされていない.
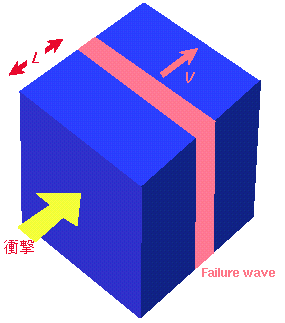
ここではべき乗分布をまず仮定して,現象論的に質量分布関数のべき指数を 導出してみよう. ここで破壊面の移動距離をLとする(右図). 十分大きな試料を考えると,歪みの伝搬距離はL程度であり, 弾性振動を特徴付けるマクロな長さもLのみとなる. 破壊面の「厚み」は十分時間が経過した後ではLに較べて無視 できるであろうし,また原子スケールの現象がマクロな破壊プロセスに 直接影響するとは考えにくい. つまり,唯一Lがこの系のマクロな長さのスケールを規定する. そこで,破壊面が通過してしまった場所(距離がLより十分小さい範囲) では分布関数はべき乗的に,破壊面がまだ通過していない部分で は破片が生じないことを考慮して,質量分布関数n(m,L)を 以下のように書いてみる.
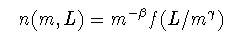 (4)
(4)
破壊面がLだけ進行した場合に,すでに壊れてしまった部分の 質量は,分布関数の定義から
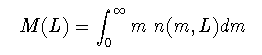 (5)
(5)
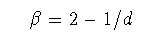 (6)
(6)
指数βは破壊面の広がり方には依らないのであろうか? 破壊面が円筒状の試料の中心軸から円筒状に広がるケースを考えると, 上の議論でM(L)はL2に比例すべきであって, 同様に指数の比較を行うと,β=4/3が得られる. また,球面状の破壊面の場合はβ=1となるべきである. このことは,破片の質量分布が試料の次元性とともに,波面の広がり方, すなわち衝撃の加え方にも強く依存する可能性を示唆している. 事実,岩石や氷などの破壊実験においてはbの値が条件によって 大きくばらつく事例もあり,「壊し方」と「壊れ方」の関係について の実験的な検討にも興味が持たれる.
破壊は,古くて新しい問題である. 経験に基づいて宝石職人は見事に原石をカットすることが出来るが, 物理的な観点からは理想的な結晶中を走る一本の亀裂の振る舞いでさえ まだ十分に理解されていないのが現状である. コンピュータの発達で従来は見えなかった事実が明らか にされていくには違いないし,実験技術の向上も期待されるが, 一本のチョークがどのように割れるのかを我々が本当に理解した 気持ちになれるのはもう少し先のことかもしれない. 破壊現象に関する研究のいっそうの展開を期待したい.