フォッカー・プランク方程式

このページでは、確率微分方程式（ランジュバン方程式）と確率分布の時間発展を記述するフォッカー・プランク方程式について考えてみる。（書きかけ）

ランジュバン方程式からフォッカー・プランク方程式の導出

「粒子」の時刻 $t$ での位置を $x(t)$とし、 平均が0、自己相関が$R$であるような揺動項 $\xi(t)$ を含んだランジュバン方程式 $$ \frac{d x(t)}{dt} = f(x) + \xi(t) \tag{1} $$ を考えてみる。

ここで、$x(t)$のある関数 $h(x,t)$ を考える。 $x(t)$が確率的に変動するのであるから、$h(x,t)$も確率的に変動することになる。 ここで、時間が$\Delta t$だけ経過し、粒子が$\Delta x$移動した後の関数$h(x,t)$の変化 $ \Delta h = h(x + \Delta x,t+\Delta t) - h(x,t) $ を考えてみよう。 伊藤の補題によれば $$ \Delta h = \frac{\partial h}{\partial t} \Delta t + \frac{\partial h}{\partial x} \Delta x + \frac{1}{2} \frac{\partial^2 h}{\partial x^2} (\Delta x)^2 + \cdots $$ のように展開できる。 ここで、確率微分方程式の差分 $$ \Delta x = f(x) \Delta t + \xi(t) \sqrt{\Delta t} $$ を用い、$\Delta t$ について一次のオーダーまでを残すと $$ \Delta h = \frac{\partial h}{\partial t} \Delta t + \frac{\partial h}{\partial x} \left( f(x) \Delta t + \xi(t) \sqrt{\Delta t} \right) + \frac{1}{2} \frac{\partial^2 h}{\partial x^2} \xi^2(t) \Delta t $$ となる。 $\xi$についての平均を記号 $\langle \cdot \rangle$ で表すことにして、 仮定 $\langle \xi \rangle = 0$, $\langle \xi^2 \rangle = R$ を使いながら、各項の平均を取ると $$ \left\langle \Delta h \right\rangle = \left\langle \frac{\partial h}{\partial t} \right\rangle \Delta t + \left\langle \frac{\partial h}{\partial x} f(x) \right\rangle \Delta t + \frac{R}{2} \left\langle \frac{\partial^2 h}{\partial x^2} \right\rangle \Delta t $$ となる。 さらに 全体を $\Delta t$ で割って、$\Delta t \to 0$ を取ると $$ \frac{d \langle h \rangle}{dt} = \left\langle \frac{\partial h}{\partial t} \right\rangle + \left\langle \frac{\partial h}{\partial x} f(x) \right\rangle + \frac{R}{2} \left\langle \frac{\partial^2 h}{\partial x^2} \right\rangle \tag{2} $$

同様な粒子が多数ある、あるいは、多数回の試行を繰り返しているような状況を想定しつつ、 このような粒子が時刻$t$に座標$x$に存在する確率密度 $p(x,t)$ について考えてみよう。 粒子は空間の必ずどこかには存在する（生成や消滅はしない）ので、時刻によらず $$ \int p(x,t) dx = 1 $$ でなければならない。

この確率密度を使うと、各時刻での平均量は $$ \left\langle \cdot \right\rangle = \int p(x,t) \cdot dx $$ に他ならないから、式(2)は $$ \frac{d}{dt} \int p(x,t) h(x,t) dx = \int p(x,t) \frac{\partial h}{\partial t} dx + \int p(x,t) \frac{\partial h}{\partial x} f(x) dx + \frac{R}{2} \int p(x,t) \frac{\partial^2 h}{\partial x^2} dx \tag{3} $$ と書ける。 このとき左辺は $$ \frac{d}{dt} \int p(x,t) h(x,t) dx = \int \frac{\partial p(x,t)}{\partial t} h(x,t) dx + \int p(x,t) \frac{\partial h(x,t)}{\partial t} h dx $$ 式(3)右辺の第二項は、$x$について部分積分して、 $$ \int p(x,t) \frac{\partial h}{\partial x} f(x) dx = \left[ h(x,t) p(x,t) f(x,t) \right]^\infty_{-\infty} - \int h(x,t) \frac{\partial \{p(x,t) f(x)\}}{\partial x} dx $$ となるが、$\lim_{x \to \pm \infty} p(x,t)=0$を仮定すると、上式の右辺は第二項のみが残る。 同様に、式(3)の二階微分の項も部分積分を繰り返して、無限遠で確率密度とその微分が0となるような境界条件を仮定することで $$ \int p(x,t) \frac{\partial^2 h(x,t)}{\partial x^2} dx = \int h(x,t) \frac{\partial^2 p(x,t)}{\partial x^2} dx $$ となる。 以上の式を整理すると式(3)は $$ \int h(x,t) \frac{\partial p(x,t)}{\partial t} dx = - \int h(x,t) \frac{\partial \{p(x,t) f(x)\}}{\partial x} dx + \frac{R}{2} \int h(x,t) \frac{\partial^2 p(x,t)}{\partial x^2} dx $$ のように変形できるが、これが$h(x,t)$の選び方に依らずに成り立つことから、$h(x',t') = \delta(x'-x) \delta(t'-t)$ とおけば、確率分布の時間発展は $$ \frac{\partial p(x,t)}{\partial t} = - \frac{\partial \{p(x,t) f(x)\}}{\partial x} + \frac{R}{2} \frac{\partial^2 p(x,t)}{\partial x^2} \tag{4} $$ に従うことがわかる。この微分方程式はフォッカー・プランク方程式(Fokker-Planck equation)と呼ばれている。

ここで、確率の流れを $$ J(x,t) = f(x) p(x,t) - \frac{R}{2} \frac{\partial p(x,t)}{\partial x} $$ と定義すると、フォッカープランク方程式は確率流についての保存の式、すなわち $$ \frac{\partial p(x,t)}{\partial t} + \nabla \cdot J = 0 $$ に他ならない。

ポテンシャル中のランダムウォーク

では、$f(x)$がやや特殊な（けれども、よくある）形の場合について考えてみよう。 それは $$ f(x) = - \frac{\partial U(x)}{\partial x} $$ となるケースである。ここで$U(x)$をポテンシャル関数と呼ぶことにしよう。

このとき、フォッカー・プランク方程式の定常解 $\frac{\partial p}{\partial t}=0$ は $$ \frac{d}{d x} \left\{ p(x) \frac{d U(x)}{d x} \right\} + \frac{R}{2} \frac{d^2 p(x)}{d x^2} = 0 $$ この式を$x$で積分すると、積分定数を$C$として $$ p(x) \frac{d U(x)}{d x} + \frac{R}{2} \frac{d p(x)}{d x} = C $$ となる。 明らかにその解は、規格化定数を$A$とすると $$ p(x) = A e^{-\beta U(x)} $$ の形をしており、 $$ \beta = \frac{2}{R}, \,\,\, C=0 $$ であることがわかる（代入して確かめてみよ）。

すなわち ポテンシャル$U(x)$中でのランダムウォークの定常分布は $$ p(x) \sim e^{-\frac{2}{R} U(x)} $$ となる。

特に、調和ポテンシャル（$U(x) = \frac{B}{2} x^2$）の場合は、オルシュタイン・ウーレンベック過程と呼ばれ、その定常分布はガウス分布 $$ p(x) \sim e^{-\frac{2 B x^2}{R}} $$ となる。

以上から、定常分布が $p(x)$ となるように、ポテンシャル関数を $$ U(x) = - \frac{R}{2} \log p(x) $$ のように「設計」することもできる。 系のダイナミクスに影響するのは$U(x)$の微分であるから、定数項は任意であって、ここでは$0$とおいた。

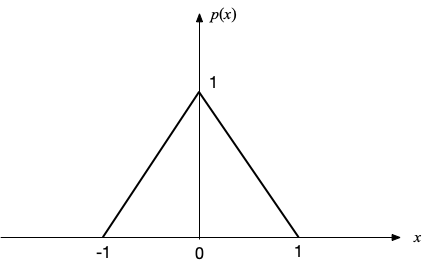
では、定常分布が図のような三角型になるように$U(x)$を決めてみよう。

離散的なランジュバン方程式は $$ x(t+\Delta t) = x(t) + \frac{R}{2} \frac{\partial \log p(x)}{\partial x} \Delta t + \xi(t) \sqrt{\Delta t} $$ となり、この場合、区間 $-1 \lt x \lt 0$では、$\partial_x \log p(x)=1/(x+1)$、 $0 \lt x \lt 1$では $\partial_x \log p(x)=-1/(1-x)$で、 その他の区間では $\partial_x \log p(x)=0$ である。 以下はそのPythonコードの例である。

import matplotlib.pyplot as plt
import random
import math

def dlogp_dx(x):
    if x<-1:
        return 0
    elif x<0:
        return 1/(x+1)
    elif x<1:
        return -1/(1-x)
    else:
        return 0

xlist = []    

R = 1.0
dt = 0.01
t = 0 
t_max = 1000

x=0.0

while t<t_max:
    dx = R/2 * dlogp_dx(x) * dt + random.gauss(0,1) * math.sqrt(R*dt)
    x = x + dx
    xlist.append(x)
    t = t + dt

plt.hist(xlist,bins=100, range=(-2,2), density=True)
plt.xlabel('x')
plt.ylabel('p(x)')
plt.show()

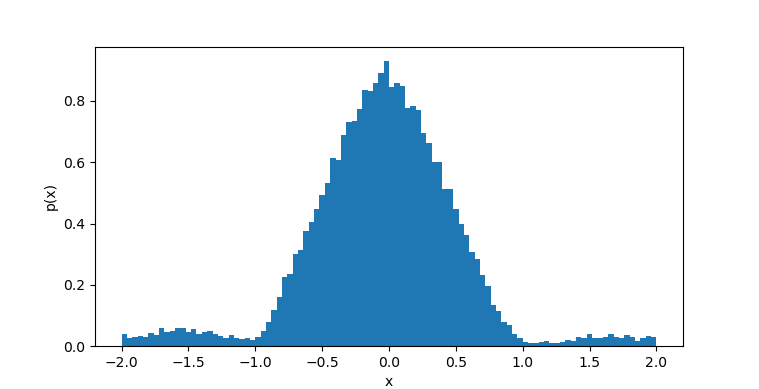
このプログラムは、最後に生成される$x$の系列のヒストグラムをプロットするようになっており、以下はその結果の例で、三角型の分布となっていることが確認できる。 このように、ランジュバン方程式を使った粒子の拡散過程を用いて、ある確率分布に従った状態をサンプリングすることができるわけである。

調和ポテンシャル中の拡散過程

調和ポテンシャル $U(x)=\frac{B}{2} x^2$ 中の粒子の拡散を表すフォッカープランク方程式 $$ \frac{\partial P(x,t)}{\partial t} = B \frac{\partial \{ x P(x,t)\}}{\partial x} + D \frac{\partial^2 P(x,t)}{\partial x^2} $$ の解について調べてみよう。

初期条件がデルタ関数 $$ P(x,0) = \delta(x-x_0) $$ で与えられるような解を$G(x,t|x_0)$と表記して（これはグリーン関数と呼ばれている）、 $G(x,t|x_0)$がどのような形になるのかを考えることにする。 グリーン関数のフーリエ変換を $$ \hat{G}(k,t|x_0) = \int G(x,t|x_0) e^{-i k x}dx $$ と定義し、フォッカープランク方程式を $\hat{G}$ をつかって書き直すと $$ \frac{\partial}{\partial t} \hat{G} = - B k \frac{\partial \hat{G}}{\partial k} - D k^2 \hat{G} $$ となる （フーリエ変換の性質：${\cal F}\left[\frac{d G(k,t)}{d x}\right] = i k G(k,t)$, ${\cal F} \left[x G(x,t)\right] = i \frac{\partial \hat{G}}{\partial k}$ を用いた）。 さらに全体を$\hat{G}$で割って、対数微分の形にすると、 $$ \frac{\partial}{\partial t} \log \hat{G} = - B k \frac{\partial}{\partial k} \log \hat{G} - D k^2 \tag{5} $$ を得る。

この状況で拡散粒子は、原点方向に向かって平均位置が移動しつつ、分布の広がりは大きくなっていくだろう。 そこで、天下り的ではあるが、時刻$t$での平均位置を$\mu(t)$、 分散を$S(t)$とおいて、時刻$t$での分布がガウス分布に従うものと仮定してみる。 平均 $\mu$、分散$S$のガウス分布関数のフーリエ変換は $$ \exp\left( - i k \mu - \frac{1}{2} S k^2 \right) $$ となるので、$\log \hat{G}$が $$ \log \hat{G} = - i k \mu(t) - \frac{1}{2} S(t) k^2 $$ という形をしているものとして、式(5)に代入すると $$ - i k \frac{d \mu(t)}{dt} - \frac{1}{2} k^2 \frac{d S(t)}{dt} = i k B \mu(t) + B k^2 S(t) - D k^2 $$ を得る。 これが恒等的に成り立つためには $$ \frac{d \mu(t)}{dt} = - B \mu(t) $$ かつ $$ \frac{d S(t)}{dt} = -2 B S(t) + 2 D $$ が成立していればよい。 ここで初期条件（デルタ関数。その分散は無限小）、 $$ \mu(0) = x_0, \;\; S(0) = 0, $$ を思い出すと、（うまい具合に）解として $$ \mu(t) = x_0 e^{-B t} $$ $$ S(t) = \frac{D}{B} \left( 1 - e^{-2 B t}\right) $$ が得られる

改めてグリーン関数（デルタ分布から出発した確率分布）を書き下すと $$ G(x,t) = \sqrt{\frac{B}{2 \pi D \left( 1 - e^{-2 B t}\right)}} \exp\left[ -\frac{B (x - x_0 e^{-B t})^2}{2 D \left( 1 - e^{-2 B t}\right)} \right] $$ となる。

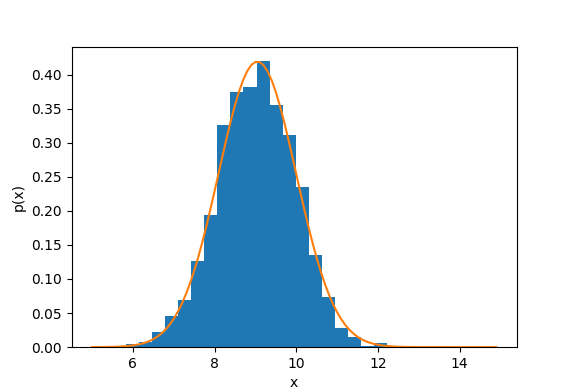
ランジュバン方程式で生成した多数のサンプルと、上記の解を比較して表示するPythonコードの例を以下に示す：

import matplotlib.pyplot as plt
import random
import math
import numpy as np

R = 1.0
x0 = 10
B = 0.1
def pdist(x,t):
    D = R/2
    mu=x0*math.exp(-B*t)
    S= D*(1-math.exp(-2*B*t))/B
    return math.sqrt(1/(math.pi*2*S)) *  np.exp( -(x-mu)*(x-mu)/(2*S) )
          
t0 = 0 
t1 = 1
dt = 0.01

xlist = []    
ntrial = 0
while ntrial<2000:
    x=x0
    t=t0    
    while t<t1:
        dx = -B * x * dt + random.gauss(0,1) * math.sqrt(R*dt)
        x = x + dx
        t = t + dt
    ntrial += 1
    xlist.append(x)    

xs=np.arange(5,15,0.1)
ps=pdist(xs,t1)
    
plt.hist(xlist,bins=20,density=True)
plt.plot(xs,ps)
plt.xlabel('x')
plt.ylabel('p(x)')
plt.show()