待ち行列

このページでは、待ち行列についてあれこれ試行してみる（ここはこれから）。

ポアソン過程

ある瞬間に発生するイベントを考えよう。例えば、コンビニに客が入店する、原子が崩壊する、パソコンのLANポートに信号（パケット）が到着する、等々。

ある時刻$t$から、わずかな時間間隔$\Delta t$の間に、それらのイベントが発生する確率が時間間隔に比例する、すなわち $$ p(t ; t+\Delta t) = \lambda \Delta t + O(\Delta t^2) $$ であるような場合について考えてみよう。 すると、イベントが発生しない確率は $$ q(t; t+\Delta t) = 1 - \lambda \Delta t + O(\Delta t^2) $$ ということになる。

$t=0$から$\tau=n \, \Delta t$の間の$n$個の等間隔な区間で、合計$k$回のイベントが発生する確率$P_k(0;\tau)$を考える。 それぞれの区間での事象が互いに独立と仮定できる場合は、$\Delta t = \tau/n$であるから、 $$ P_k (0;\tau) = {n \choose k} p^k q^{n-k} \\ = \frac{n!}{k! (n-k)!} \left( \frac{\lambda \tau}{n} \right)^k \left( 1- \frac{\lambda \tau}{n} \right)^{n-k} $$ となる（$\Delta t$ より高次の項は省いた）。 これを少し変形すると $$ \begin{eqnarray} & = & \frac{n (n-1) \cdots (n-k+1)}{k!} \frac{(\lambda \tau)^k}{n^k} \left( 1 - \frac{\lambda \tau}{n} \right)^n \left( 1 - \frac{\lambda \tau}{n} \right)^{-k} \\ & = & \frac{n (n-1) \cdots (n-k+1)}{n^k} \frac{(\lambda \tau)^k}{k!} \left( 1 - \frac{\lambda \tau}{n} \right)^n \left( 1 - \frac{\lambda \tau}{n} \right)^{-k} \end{eqnarray} $$ となるが、式中の各部品について $$ \begin{eqnarray} \lim_{n\to\infty} \frac{n (n-1) \cdots (n-k+1)}{n^k} = 1 \\ \lim_{n\to\infty} \left( 1 - \frac{\lambda \tau}{n} \right)^n = e^{-\lambda \tau} \\ \lim_{n\to\infty} \left( 1 - \frac{\lambda \tau}{n} \right)^{-k} = 1 \end{eqnarray} $$ となることから、$n \to \infty$（あるいは$\Delta t \to 0$）の極限で、 $$ P_k(0;\tau) = \frac{(\lambda \tau)^k e^{-\lambda \tau}}{k!} $$ を得る。この確率は時間の原点には依らないので、改めて $$ P_k(\tau) = \frac{(\lambda \tau)^k e^{-\lambda \tau} }{k!} $$ と表記することにしよう。

このような確率（ポアソン分布）で独立にイベントが生じる過程をポアソン過程と呼ぶ。 過去のイベントに現在のイベントが全く影響されず、イベントが「点」と見做せるような例は枚挙にいとまがないが、 そういったケースではポアソン過程が基本的なモデルとなる。

時間軸上にイベントが発生した点を打っていったとして、その点の間隔はどのような分布になっているだろうか。 イベントが起こった時点を起点として、その時間$\tau$から$\tau + \Delta \tau$のあいだイベントが１回発生する確率がそれであるから $$ p_1(\tau) \Delta \tau = q^n p = \left(1-\frac{\lambda \tau}{n}\right)^n \lambda \Delta \tau $$ となるので、$n \to \infty$を取って $$ p_1(\tau)d\tau = e^{-\lambda \tau} \lambda \, d\tau $$

あるいは、全く同じことではあるが、 $$ p_1(\tau) d\tau = \lim_{\Delta \tau \to 0} \frac{P_1(\tau+\Delta \tau)-P_1(\tau)}{\Delta \tau} d\tau = \frac{d P_1(\tau)}{d\tau} \, d\tau = \lambda e^{-\lambda \tau} \, d\tau $$

このように、ポアソン過程でのイベント間隔は指数分布となることがわかった。

このときのイベント間隔の平均 $\bar{\tau}$ は $$ \bar{\tau} = \int_0^\infty \tau \, \lambda e^{-\lambda \tau} \, d\tau = \frac{1}{\lambda} $$ である。

　参考: アーラン分布

ある客と次の客の来店間隔が指数分布に従う場合、$n$人の客が来る間隔の分布はどのようになるだろうか。

指数分布の特性関数（ラプラス変換） $$ E[e^{-s \tau}] = \int_0^\infty p_1(\tau) e^{-s \tau} d\tau = \int_0^\infty \lambda e^{-\lambda \tau} e^{-s \tau} d\tau = \frac{\lambda}{s + \lambda} $$ を考えると、 指数分布に従う独立な確率変数 $\tau_i$ の$n$個の和 $$ \tau = \tau_1 + \cdots + \tau_n $$ の特性関数は $$ \Phi_n(s) = \left[ \frac{\lambda}{s + \lambda} \right]^n $$ となる。

そのラプラス逆変換は（複素積分を行うことで） $$ \frac{1}{2 \pi i} \int_{- i \infty}^{+ i \infty} \Phi_n(s) e^{s \tau} ds = \underset{s=-\lambda}{\mathrm{Res}} \left[ \frac{\lambda^n e^{s \tau}}{(s + \lambda)^n} \right] \\ = \lambda^n \frac{1}{(n-1)!} \lim_{s \to -\lambda} \frac{d^{n-1}}{ds^{n-1}} e^{s \tau} = \frac{\lambda^n \, \tau^{n-1} \, e^{-\lambda \tau}}{(n-1)!} $$ となる。こうして得られた確率密度 $$ f(\tau ; n, \lambda) = \frac{\lambda^n \, \tau^{n-1} \, e^{-\lambda \tau}}{(n-1)!} $$ はアーラン分布（Erlang distribution）と呼ばれている。

レジの順番待ち（直接的シミュレーション）

コンビニやスーパーのレジの順番待ちをシミュレーションしてみよう。簡単のため、レジは１つの場合に限る。

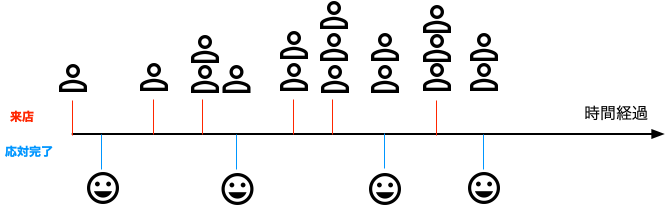
客は（それぞれがポアソン過程と見なせる、という意味において）ランダムにレジに向かい、店員がひとりの客に対応するのに要する時間もランダムであるとしよう。 そして、客が並ぶ平均時間間隔を$\tau_c$、店員の対応時間の平均を$\tau_s$ と置くことにする。

ある時刻$t$にレジ待ちの客が0人の状態で、一人の客が並んだとしよう。 すると、次に客がレジに来るのは、そこから起算して、 $$ t_c = t + \xi $$ の時点ということになる。ここで$\xi$は平均$\tau_c$の指数分布に従う確率変数である。 そのとき、その客の対応が完了する時刻は、平均$\tau_s$の指数分布に従う確率変数$\eta$を使って、 $$ t_s = t + \eta $$ と表せる。

レジに１人以上の客が並んだ状態では、接客中に別の客が新たに加わる場合と、待っている客への対応が完了する（すなわち列が１人減る）場合がある。

別の客が並ぶのは $t_c \lt t_s$ の場合で、その場合、さらに次の客が並ぶタイミングは $$ t_c \leftarrow t_c + \xi $$ に更新される。

他方で、列から１人減るのは $t_c \gt t_s$ の場合で、次の客への対応が完了するタイミングは $$ t_s \leftarrow t_s + \eta $$ となる。

これを直接シミュレーションするには、平均を指定した指数分布に従う乱数を生成する必要があるが、 こちらのページに書いたように、$(0,1]$区間の一様乱数を$X$から $$ Y = -\tau \log(X) $$ によって得られる。 たとえば、randomモジュールの一様乱数random.random()は0以上、1未満の実数を返すので、指数分布の乱数を

import random
import math
tau = 2.0
Y = - tau*math.log(1-random.random())

のように記述できる。1から引き算するのは、対数の引数が0になるのを防ぐためである。

以上を踏まえて書いたコードの例を以下に示す：

# coding: utf-8                                                                                                                                                                                                                               

import math
import random
import matplotlib.pyplot as plt

tau_c = 10.0
tau_s = 5.0

t = 0
tc = 0
nq = 0

T=[ ]
NQ=[ ]

while t<1000:
    nqprev=nq
    if nq==0:
        xi = -tau_c*math.log(1-random.random())
        t = tc
        nq = 1
        tc += xi
        eta = -tau_s* math.log(1-random.random())
        ts = t + eta
    else:
        if tc <= ts:
            xi = -tau_c*math.log(1-random.random())
            if tc != ts:
                nq += 1
            t = tc
            tc += xi
        elif tc > ts:
            eta = -tau_s*math.log(1-random.random())
            nq -= 1
            t = ts
            ts += eta
    T.append(t)
    NQ.append(nqprev)
    T.append(t)
    NQ.append(nq)

plt.plot(T,NQ, color=(1.0,0.0,0.0), linewidth=1.0)
plt.xlabel('TIME')
plt.ylabel('NQ')
plt.grid(True)
plt.show()

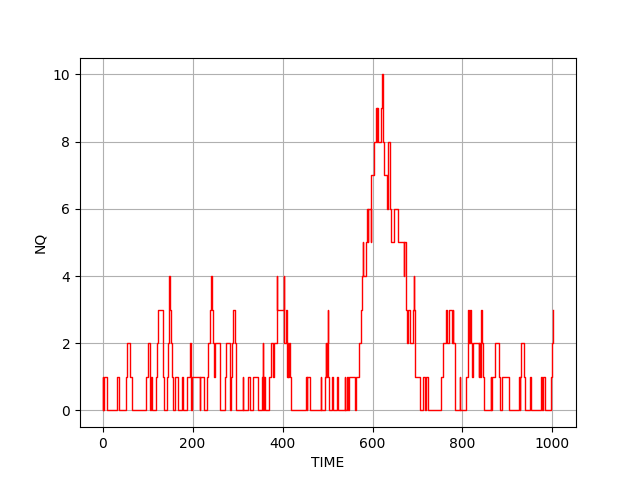
以下は $\tau_c=10, \, \tau_s=5$の場合のシミュレーション例である。 横軸が時間、縦軸がレジ待ち人数を表す。 確率的に、ときおり列が長くなる場合があることが分かる。

マスター方程式

レジ待ちは、待ち人数が0人の場合、1人の場合、・・・、と状態が場合分けできる。 時刻$t$で$n$人が並んでいる状態の確率を $$ P_n(t) $$ と表記することにしよう。定義から $$ \sum_{n=0}^{\infty} P_n(t) = 1 $$ である。

$\lambda = 1/\tau_c$, $\mu = 1/\tau_s$ とすると、これらの確率の時間変化は、 $$ \frac{d P_0(t)}{dt} = \mu P_1(t) - \lambda P_0(t) $$ $n \ge 1$の場合は、 $$ \frac{d P_n(t)}{dt} = \mu P_{n+1}(t) - (\lambda + \mu) P_{n}(t) + \lambda P_{n-1}(t) $$ と表すことができる（マスター方程式、あるいはコルモゴロフの微分方程式）。

マスター方程式に定常解（微分が０となる解）が存在すると仮定して、それらを$P_0, P_1, \cdots, P_n, \cdots$と置くと、 漸化式 $$ \begin{eqnarray} 0 & = & \lambda P_0 - \mu P_1 \\ 0 & = & \mu P_{n+1} - (\lambda + \mu) P_n + \lambda P_{n-1} \end{eqnarray} $$ ここで、$\alpha = \lambda/\mu$ を定義して、式を整理すると $$ \begin{eqnarray} P_1 & = & \alpha P_0 \\ P_{n+1} - P_{n} & = & \alpha ( P_n - P_{n-1}) \end{eqnarray} $$ となるから、$P_{n+1} - P_n$は等比数列で表現できることが分かって、初項を考慮すると $$ P_n = P_0 \alpha^{n} $$ が得られる。 確率の保存 $\sum_{n=0}^\infty P_n = 1$より $$ P_0 = 1 - \alpha $$ でなければならないから、結局 $$ P_n = \left( 1 - \frac{\lambda}{\mu} \right) \left( \frac{\lambda}{\mu} \right)^{n} $$ が得られた。 定常解が存在するための必要条件として、$\lambda/\mu \lt 1$、すなわち、客の平均到来時間よりも、レジの処理時間のほうが短くなければならない。 これは、自然な結果であろう。

定常状態でのレジ待ちの長さの平均は $$ L = \sum_{n=0}^{\infty} n P_n = (1-\alpha) \sum_{n=0}^{\infty} n \alpha^{n} $$ ここで、 $$ F(\alpha) = \sum_{n=0}^{\infty} \alpha^{n} = \frac{1}{1-\alpha} $$ とおくと、 $$ \alpha \frac{d F(\alpha)}{d \alpha} = \alpha \sum_{n=0}^\infty n \alpha^{n-1} = \frac{\alpha}{(1-\alpha)^2} $$ であるから、 $$ L = \frac{\alpha}{1-\alpha} = \frac{\lambda}{\mu - \lambda} $$ となり、$\alpha \to 1$で発散することがわかる。

　練習：分散

レジ待ちの長さの分散を求めてみなさい。

　練習：シミュレーションとの比較

モンテカルロシミュレーションでレジ待ちの時間平均と分散を求め、この節での計算結果と比較してみなさい。

　参考：列を変わるべきか

複数のレジに列ができているとき、人数の少ない列に並び直したくなることがよくある。

時間あたり$\mu$人への対応が可能なレジに並んでいる$n$人目の客の待ち時間は、（$n$人の客が来店する時間間隔と同様）アーラン分布となって、 $$ f(\tau ; n, \mu) = \frac{\mu^n \, \tau^{n-1} \, e^{-\mu \tau}}{(n-1)!} $$ となる。 待ち時間の平均は $$ \bar{\tau} = \int_0^\infty \tau \, f(\tau ; n, \mu) d\tau = \frac{n}{\mu} $$ である（確かめてみよ）。

そうすると、レジ1の処理能力と待ち人数をそれぞれ$\mu_1, \, n_1$、レジ2では$\mu_2, \, n_2$として、 $n_1 \lt n_2$だからといってレジ1に並ぶのは得策ではなく、 $$ \frac{n_1}{\mu_1} \lt \frac{n_2}{\mu_2} $$ でない限り、レジ1に並ぶと時間の無駄になる可能性が高い、という結論になる（レジ担当者によって作業の速度が目に見えて違うのはよくあることである）。

（以下、書きかけ）