Pythonプログラミング（ステップ７・各種分布に従う乱数の生成）

このページでは、様々な分布に従う乱数の発生法について考える。

1. 一様乱数から変数変換する

Pythonコードのはじめに、

import random

と書いてrandomモジュールを読み込むと　random.random() で、0から1の範囲（1は含まない）のランダムな実数が得られる。 これを確率変数$X$で表すと、確率密度関数は $$ f(x) = \begin{cases} 1 & (0 \le x \lt 1) \\ 0 & (\textrm{otherwise}) \end{cases} $$ である。

ここで、この$X$を使って $ Y=-\log(X)$ によって変換すると、$Y$はどのような分布関数に従うだろうか。 $Y$の確率密度関数を$g(y)$とすると $$ g(y) = \int \delta\left( y - (- \log(x)) \right) f(x) dx = \int_0^1 \delta\left( y + \log(x) \right) dx $$ となるから、$t = y + \log(x)$と変数変換すると、 $$ g(y) = \int_{-\infty}^y \delta\left( t\right) e^{t - y} dt = e^{-y} $$ となって、$Y$は$[0, \infty]$で指数分布することがわかる。

もっと一般に、$Y = h(X)$ によって確率変数を変換すると $$ g(y) = \int_0^1 \delta\left( y - h(x) \right) dx $$ $t = y - h(x)$と変数変換すると、$x = h^{-1}(y-t)$ であるから、 $$ \begin{eqnarray} = \int \delta(t) \left| \frac{dx}{dt} \right| dt = \int \delta(t) \left| \frac{d h^{-1}(y-t)}{dt} \right| dt \\ = \int \delta(t) \left| \frac{d h^{-1}(y-t)}{dy} \right| dt = \left|　\frac{d h^{-1}(y)}{dy}　\right| \end{eqnarray} $$ となる。 すなわち、$h(x)$ の逆関数 $h^{-1}(y)$ の微分によって、変換後の分布関数が得られる。

以上のプロセスを逆にたどると、一様分布 $X$ を $Y = h(X)$ で変換した結果、$Y$の分布を$g(y)$とするためには、 まず $g$ を積分し（積分の下限は$Y$の下限にとる）、 $$ h^{-1}(y) = G(y) = \int^y g(y) dy $$ その逆関数 $G^{-1}$ によって $$ h(x) = G^{-1}(x) $$ とすればよい。

この方法は、$g$の不定積分と、その逆関数が必要という点で、応用範囲は限られる。

　練習：べき乗分布

$[1,\infty] $の区間で $g(y)=y^{-2}$ の分布関数に従う乱数を、$[0,1]$の一様乱数から生成する方法を考えなさい。

　練習：コーシー分布

$[-\infty,\infty] $の区間で $g(y)= \frac{1}{\pi} \frac{1}{1 + y^{2}}$ の分布関数に従う乱数を、$[0,1]$の一様乱数から生成する方法を考えなさい。

２. 棄却法

目的とする分布関数の積分とその逆関数を見つけるのは、一般には、容易でない。そのような場合は、 少し効率は劣るものの、棄却法(rejection method)を用いることができる。

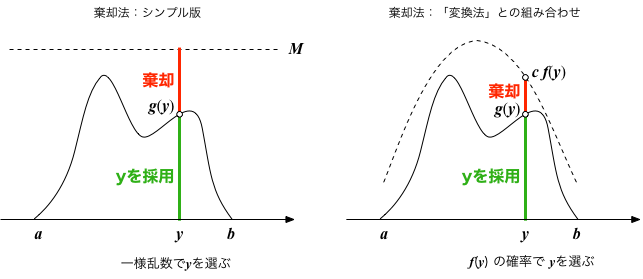
棄却法：シンプルバージョン

1. 区間$[a,b]$で定義された（目的とする）密度関数を$g(y)$とする。$g(y)$の最大値を超えるある数を$M$とする。
2. $[a,b]$の区間で一様乱数を生成し、その値を$y$とする
3. $[0,M]$の一様乱数を生成し、その値を$t$とする
4. $g(y) \lt t $ なら $y$ を出力する。そうでなければ、何も出力しない（棄却する）。
5. ステップ2からを繰り返す

棄却法：「変換法」との組み合わせ

1. 区間$[a,b]$で定義された（目的とする）密度関数を$g(y)$とする。
2. $c$を定数として、区間$[a,b]$内で $g(y) \lt c \, f(y)$ となるような「ちょうど良い」密度関数 $f(y)$ を用意する。その積分を $F(y) = \int_a^y f(y) dy$、その逆関数を $F^{-1}(x)$ とする。
3. $[0,1]$の区間で一様乱数を生成し、それを$x$とする
4. $y = F^{-1}(x)$ を求める
5. $[0,c \, f(y)]$の一様乱数を生成し、その値を$t$とする
6. $g(y) \lt t $ なら $y$ を出力する。そうでなければ、何も出力しない（棄却する）。
7. ステップ3からを繰り返す

　練習：棄却法

図を参考に、上記のアルゴリズムがうまく働く理由を考察しなさい。

　発展：ガンマ分布

ガンマ分布（の一種）である $g(y)= \frac{1}{2} y^2 \exp(-y)$ に従う乱数を生成させるPyhonコードを書いてみなさい。$y$の定義域は$[0, \infty]$とする。

　ヒント

３. 離散的な確率変数のシミュレーション

離散的な値 $0,1,\cdots,n-1$ を取る確率変数 $X$ を考える。 ここで、それぞれの値の出現確率が $p(x)$ ($x=0,1,\cdots,n-1$) とすると、 この分布に従うように乱数を発生させるにはどのようにすればよいだろうか。

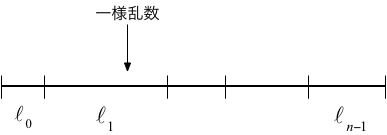
考え方はとても簡単で、$p(x)$に比例した長さ $\ell_x$ の「棒」を並べ、 その上から一様な確率で「矢」を射って、当たった区間の $x$ を出力とすればよい。

このアイデアに従って、出現確率が $p(0) = 3/40, \; p(1)=4/40, \; p(2)=10/40, \cdots$ となるように、 1から7まで数を100回出力するコードの例を以下に示した：

# coding: utf-8

import random

prob=[3, 4, 10, 8, 3, 1, 9, 2]
ptab=[ ]

psum=0
for p in prob:
    psum += p
    ptab.append(psum)

for _ in range(100):
    r = random.random()*psum
    il=-1
    ih=len(ptab)
    while True:
        if ih-il<=1:
            break
        i=(il+ih)//2
        if ptab[i]<=r:
            il=i
        else:
            ih=i

    print(ih)

まず「棒」の長さの累積値をリスト(ptab)に格納し、 変数が取り得る値の数が大きい場合も想定し、 二分検索によって、乱数がどの区間に入っているのかを調べるアルゴリズムになっている。

import numpy as np

res = np.random.choice([1,2,3], p=[0.25, 0.5, 0.25])

　練習：逆べき分布に従う整数乱数の生成

上記のサンプルを元にして、1から100までの範囲の整数 $x$ を、 ランダムに確率 $p(x) = \frac{1/x}{\sum_{n=1}^{100} {1/n}}$ で出力するコードを書いてみなさい。