Pygletによる「手抜き」OpenGL入門
5. 3次元物体の表示
5.1 正四面体モデルの構成
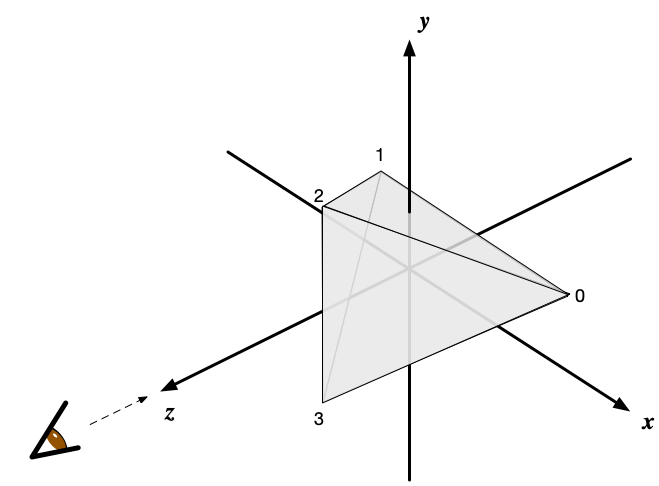
平面図形の描画は前節までにすでに学んだので、次に、正三角形を4つ組み合わせた立体、すなわち正四面体を表示してみよう。 正四面体の4つの頂点の座標は計算したり調べたりすれば簡単に知ることができて、ここでは、0番目の頂点の座標を$(1,0,-1/\sqrt{2})$, 1番目 $((-1,0,-1/\sqrt{2}))$, 2番目 $(0,1,1/\sqrt{2})$, 3番目 $(0,-1,1/\sqrt{2})$ とする。 すると、中心がちょうど原点に一致する。 それを、Z軸の正の方向から眺めたときの様子をOpenGLで生成する方法を考える。
まず必要となるのは、頂点を3つずつ組にして、三角形を構成することである。 2次元的な描画では、各頂点に色情報を与えることで彩色を施すことができたが、 3次元的な物体を表現する際には、立体的に見せるためには面に陰影をつけたいので、 それを計算するために、色情報に加え、それぞれの頂点での面の法線(単位ベクトル)も必要となる。
そこで、正四面体の頂点のリストと、頂点での法線を計算するコードをまず作成しておく。 0番目から3番目の頂点座標を組み合わせて、4つの正三角形が構成できる。三角形の3つの頂点には3つの座標成分があるから、 頂点座標データは$4 \times 3 \times 3 = 36$ 個の数値のリストとなる。
ある三角形に注目すると、各頂点での法線ベクトルは(平面なので)同一であるが、頂点毎に指定する必要があるので、冗長ではあるが、 法線についても $4 \times 3 \times 3 = 36$ 個の数値からなるリストが必要である。
0から3までの頂点座標を3つずつ組み合わせる際に、その順序も重要となる。 というのは、OpenGLでは面の向き(すなわち法線方向)を気にする必要があるためである。 実際に法線を求めるには、下図のように、三角形の辺を構成する2つのベクトルのクロス積を計算することになるが、 ベクトルを選ぶ順序で結果が文字通り180度違ってしまう。
通常、OpenGLでは面の頂点を順に辿った際に反時計回りに見える側が「表」となるように処理される。
これらに注意しながら、36個の要素からなる、頂点と法線情報のリストを生成するコードの例を以下に示す。
import numpy as np
import math
def tetrahedron():
vpos = [np.array((+1,0,-1/math.sqrt(2))), np.array((-1,0,-1/math.sqrt(2))),
np.array((0,1,1/math.sqrt(2))), np.array((0,-1,1/math.sqrt(2)))]
indices = [(0,1,2),(0,3,1),(0,2,3),(1,3,2)]
normals = []
vertices = []
for n in range(4):
i = indices[n][0]
j = indices[n][1]
k = indices[n][2]
vertices.extend([vpos[i],vpos[j],vpos[k]])
u = vpos[j] - vpos[i]
v = vpos[k] - vpos[i]
n = np.cross(u,v)
n = n/np.linalg.norm(n)
normals.extend([n,n,n])
vertices = np.concatenate(vertices).tolist()
normals = np.concatenate(normals).tolist()
return (vertices,normals)
# 正四面体モデルを生成
vertices,normals = tetrahedron()
print("Vertices=",vertices)
print("Normal_Vectors=",normals)

5.2 正四面体の表示
正四面体の頂点と法線が生成できたので、これを使って、Pygletで3次元的に表示させてみよう。 以下がコードの例である。
import numpy as np
import math
import pyglet
from pyglet.gl import *
from pyglet.math import Mat4, Vec3
from pyglet.graphics.shader import Shader, ShaderProgram
# シェーダー
# Vertex shader
vertex_source = """#version 330 core
in vec3 position;
in vec3 normals;
in vec4 colors;
out vec4 vertex_colors;
out vec3 vertex_normals;
out vec3 vertex_position;
uniform WindowBlock
{
mat4 projection;
mat4 view;
} window;
uniform mat4 model;
void main()
{
mat4 modelview = window.view * model;
vec4 pos = modelview * vec4(position, 1.0);
gl_Position = window.projection * pos;
mat3 normal_matrix = transpose(inverse(mat3(modelview)));
vertex_position = pos.xyz;
vertex_colors = colors;
vertex_normals = normal_matrix * normals;
}
"""
fragment_source = """#version 330 core
in vec4 vertex_colors;
in vec3 vertex_normals;
in vec3 vertex_position;
out vec4 final_colors;
uniform vec3 light_position;
void main()
{
vec3 normal = normalize(vertex_normals);
vec3 light_dir = normalize(light_position - vertex_position);
float diff = max(dot(normal, light_dir), 0.0);
final_colors = vertex_colors * diff * 1.2;
}
"""
window = pyglet.window.Window(width=1280, height=720, resizable=True)
window.set_caption('Tetrahedron')
batch = pyglet.graphics.Batch()
vert_shader = Shader(vertex_source, 'vertex')
frag_shader = Shader(fragment_source, 'fragment')
shader = ShaderProgram(vert_shader, frag_shader)
@window.event
def on_draw():
window.clear()
shader['model']=Mat4()
shader['light_position']=Vec3(-10,0,20)
batch.draw()
@window.event
def on_resize(width, height):
window.viewport = (0, 0, width, height)
ratio = width/height
window.projection = Mat4.orthogonal_projection(-2*ratio, 2*ratio, -2, 2, -100, 100)
return pyglet.event.EVENT_HANDLED
def setup():
glClearColor(0.3, 0.3, 0.5, 1.0)
glEnable(GL_DEPTH_TEST)
glEnable(GL_CULL_FACE)
on_resize(*window.size)
def tetrahedron(shader, batch):
vpos = [np.array((+1,0,-1/math.sqrt(2))), np.array((-1,0,-1/math.sqrt(2))),
np.array((0,1,1/math.sqrt(2))), np.array((0,-1,1/math.sqrt(2)))]
indices = [(0,1,2),(0,3,1),(0,2,3),(1,3,2)]
normals = []
vertices = []
for n in range(4):
i = indices[n][0]
j = indices[n][1]
k = indices[n][2]
vertices.extend([vpos[i],vpos[j],vpos[k]])
u = vpos[j] - vpos[i]
v = vpos[k] - vpos[i]
n = np.cross(u,v)
n = n/np.linalg.norm(n)
normals.extend([n,n,n])
vertices = np.concatenate(vertices).tolist()
normals = np.concatenate(normals).tolist()
vertex_list = shader.vertex_list(len(vertices)//3, GL_TRIANGLES, batch=batch)
vertex_list.position[:] = vertices
vertex_list.normals[:] = normals
vertex_list.colors[:] = (1.0,0.0,0.0,1.0) * (len(vertices)//3)
return vertex_list
# OpenGLの初期設定
setup()
# 正四面体モデルを生成
th_vertex_list = tetrahedron(shader,batch)
# 視点を設定
window.view = Mat4.look_at(position=Vec3(0,0,5), target=Vec3(0,0,0), up=Vec3(0,1,0))
pyglet.app.run()
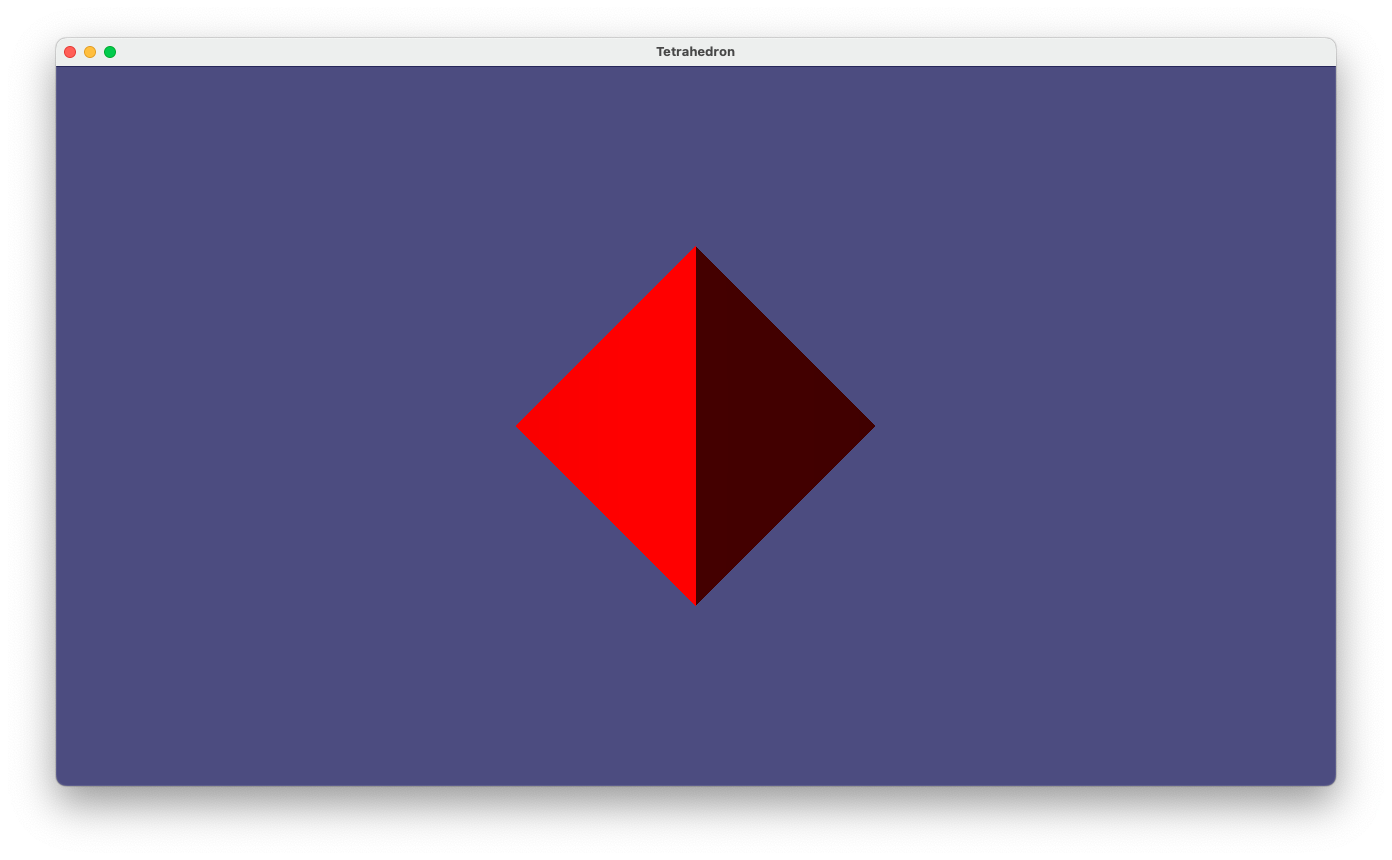
prog-5-2.pyのスクリーンショット
正四面体は、見る方向によっては、このように正方形が現れる。 このことは、正四面体は立方体の中にきっちりと収めることができることと関係している。
プログラムの基本的な構成は、2次元描画のときと変わりないので、ここでは主な変更点を上げておくことにする。
光源情報の設定
まず、シェーダーに頂点および法線ベクトルの3次元的な情報が入力できるようにする共に、簡単なライティングによる陰影が付けられるよう、 シェーダーの部分がかなり修正されている。 その内容については、節を改めて説明することにする。
陰影をつけるためには、物体がどこから照らされているのかの情報が必要となる。このコードでは on_draw()関数の中で、シェーダーに光源の位置を
shader['light_position']=Vec3(-10,0,20)
によって設定するようになっている。シェーダーでは、光源からの光線と表面の角度(方向余弦)を計算して、面の明るさを算出するようになっている。
隠面処理の設定
3次元では、奥に配置された物体は手前の物体に隠されるが、それをコンピュターで模倣する仕掛けにZバッファー方式がある。
これは、どちらがより手前の物体からの画素かを高速に判定することで、自動的に隠面処理を行う機構である。
上のコードの初期化(setup()関数)のところの
glEnable(GL_DEPTH_TEST) glEnable(GL_CULL_FACE)
は、Zバッファー機能(depth test)を有効にすると共に、裏側の面の処理を省略(カリング)することで、処理を高速化するための設定である。
頂点リストの設定
関数tetrahedron()の中で、前節の方法で頂点と法線のリストを生成した後、シェーダーに渡す頂点リストを
vertex_list = shader.vertex_list(len(vertices)//3, GL_TRIANGLES, batch=batch) vertex_list.position[:] = vertices vertex_list.normals[:] = normals vertex_list.colors[:] = (1.0,0.0,0.0,1.0) * (len(vertices)//3)
のように設定している。座標の値が3つで1つの頂点を表すので、リストの長さを3で割った値を頂点数として関数に渡している。 ここでは、全ての頂点に不透明な赤色(1.0,0.0,0.0,1.0)を指定している。
これらの頂点について情報は、頂点シェーダー(vertex_source=...)の
in vec3 position; in vec3 normals; in vec4 colors;
に対応することに注意。すなわち、positionという3次元ベクトル(vec3)、normalsという3次元ベクトル(vec3)、そしてcolorsという4次元ベクトル(vec4)を、 それぞれの頂点について与える必要があるわけだ。
視点の設定
コードの末尾付近、イベントループを開始する手前で、視点の設定
window.view = Mat4.look_at(position=Vec3(0,0,5), target=Vec3(0,0,0), up=Vec3(0,1,0))
を行っている。これによって、position の位置から target の方向に、up 方向が上になるような姿勢で物体を見ているように設定される。 これによって、内部的には、シェーダーの変数 view (次節で説明するビュー変換行列$V$)に適切な行列が設定される。

5.3 アニメーションとパースペクティブ投影
前節では、確かに正四面体を一方向から眺めることには成功したものの、立体を観察している実感は湧かなかったかもしれない。
そこで、アニメーションによって正四面体を回転させると共に、パースペクティブ(透視)投影にすることで遠近感を強調するように修正したコードが以下である。 ほとんどが前掲のprog-5-2.pyと同様なので、後半部のみを掲載する。
###
### prog-5-2.py の前半部分
### shader = ShaderProgram(vert_shader, frag_shader)
### までは prog-5-2.py と同じ
###
time=0
def update(dt):
global time
time += dt
@window.event
def on_draw():
window.clear()
shader['model']=Mat4.from_rotation(time,Vec3(1,0,0)) @ Mat4.from_rotation(time/3,Vec3(0,1,0))
shader['light_position']=Vec3(-10,0,20)
batch.draw()
@window.event
def on_resize(width, height):
window.viewport = (0, 0, width, height)
window.projection = Mat4.perspective_projection(window.aspect_ratio, z_near=0.1, z_far=255, fov=60)
return pyglet.event.EVENT_HANDLED
def setup():
glClearColor(0.3, 0.3, 0.5, 1.0)
glEnable(GL_DEPTH_TEST)
glEnable(GL_CULL_FACE)
on_resize(*window.size)
def tetrahedron(shader, batch):
vpos = [np.array((+1,0,-1/math.sqrt(2))), np.array((-1,0,-1/math.sqrt(2))),
np.array((0,1,1/math.sqrt(2))), np.array((0,-1,1/math.sqrt(2)))]
indices = [(0,1,2),(0,3,1),(0,2,3),(1,3,2)]
normals = []
vertices = []
for n in range(4):
i = indices[n][0]
j = indices[n][1]
k = indices[n][2]
vertices.extend([vpos[i],vpos[j],vpos[k]])
u = vpos[j] - vpos[i]
v = vpos[k] - vpos[i]
n = np.cross(u,v)
n = n/np.linalg.norm(n)
normals.extend([n,n,n])
vertices = np.concatenate(vertices).tolist()
normals = np.concatenate(normals).tolist()
vertex_list = shader.vertex_list(len(vertices)//3, GL_TRIANGLES, batch=batch)
vertex_list.position[:] = vertices
vertex_list.normals[:] = normals
vertex_list.colors[:] = (1.0,0.0,0.0,1.0) * (len(vertices)//3)
return vertex_list
# OpenGLの初期設定
setup()
# 正四面体モデルを生成
th_vertex_list = tetrahedron(shader,batch)
# 視点を設定
window.view = Mat4.look_at(position=Vec3(0,0,3), target=Vec3(0,0,0), up=Vec3(0,1,0))
pyglet.clock.schedule_interval(update,1/60)
pyglet.app.run()
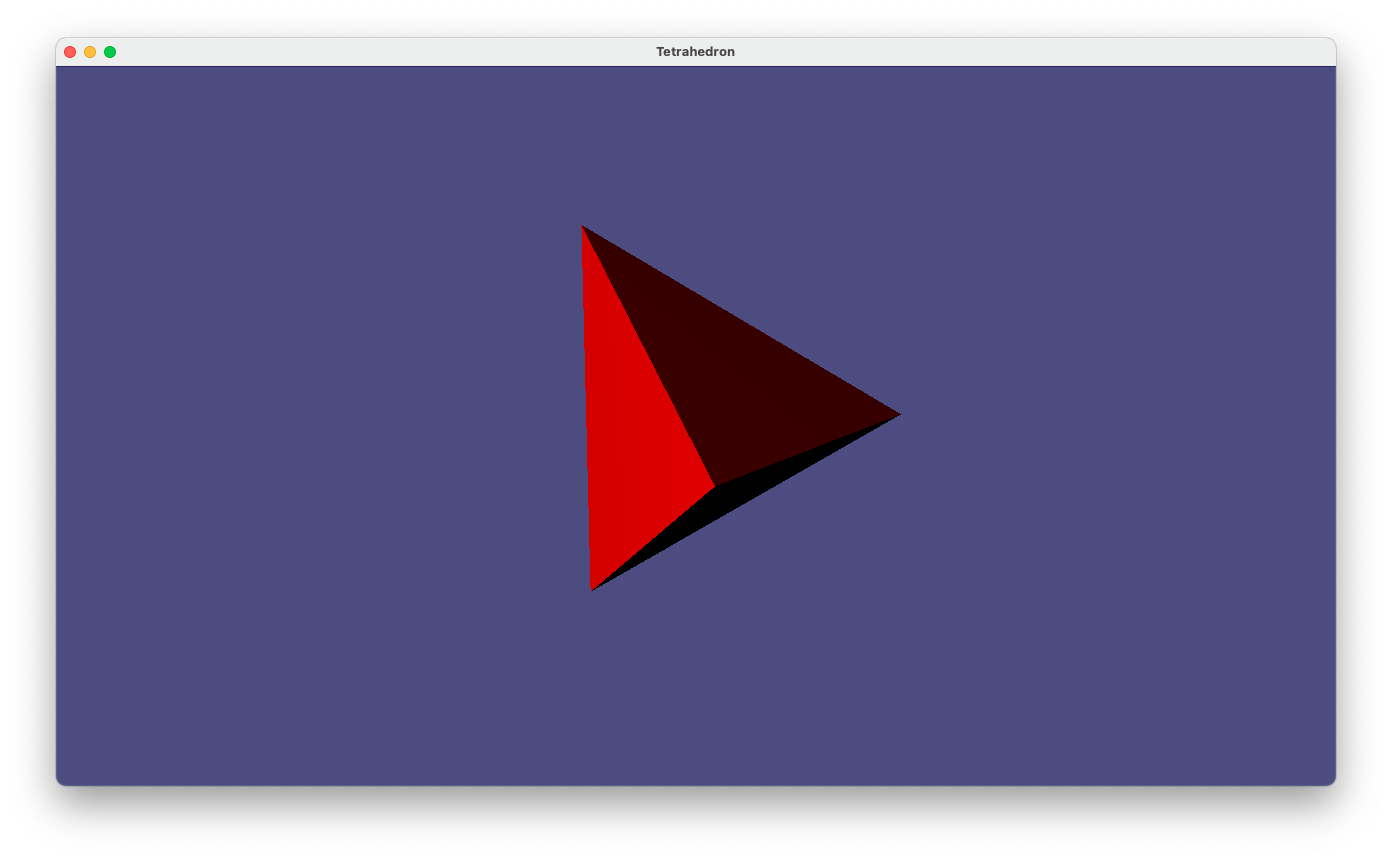
prog-5-3.pyの実行中のスナップショット
このコードではクロックを使ってupdate()関数を1/60毎に呼び出し、グローバル変数timeを更新するようになっている。
加えて、描画が必要となった都度呼び出されるon_draw()関数の中で
shader['model']=Mat4.from_rotation(time,Vec3(1,0,0)) @ Mat4.from_rotation(time/3,Vec3(0,1,0))
のようにモデル変換行列を更新している。具体的にはy軸の回りに time/3ラジアン回転し、引き続いて、x軸の回りにtimeラジアン回転することで、
「ひねり回転」のような動作を行っている。
次いで、on_resize()関数の中で、パースペクティブ投影(透視投影)を設定している:
window.projection = Mat4.perspective_projection(window.aspect_ratio, z_near=0.1, z_far=255, fov=60)
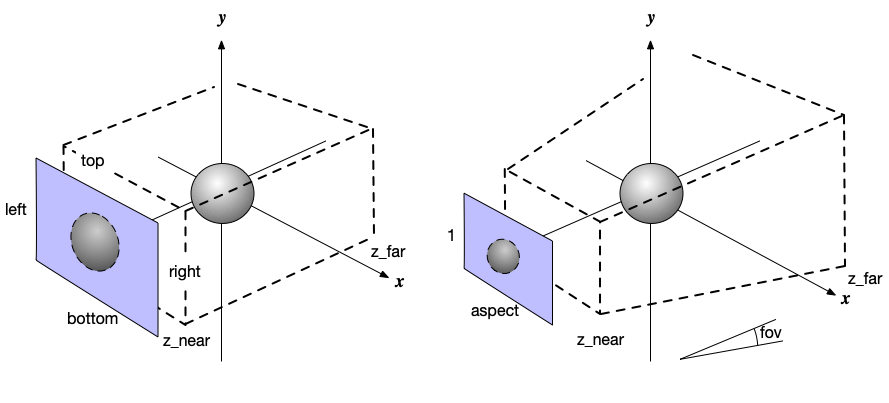
これまでの例で用いてきた投影方法は正射投影(Orthographic Projection)と呼ばれており、下図(左)のようなパラメータを設定していた。 パースペクティブ投影の様子と各パラメータの意味については、下図(右)を参照のこと。
いずれの投影法でも、破線で示した領域外に置かれた物体は描画の対象とならない(見えない)ので、各パラメータは慎重に設定しておく必要がある。
6. シェーダーの動作
6.1 同次座標系と座標変換
コンピュータグラフィックスにおいて、同次座標系(homegeneous coodinates)がよく使われるので、シェーダーの動作に入る前に、簡単に説明しておく。
3次元の列ベクトル $\boldsymbol{r} = \begin{pmatrix} x \\ y \\ z \\ \end{pmatrix} $ を考えると、それを対して原点を中心とした線形な回転、反転、収縮や変形を施す操作は、3行3列の行列 $R$ を使って $$ R \, \boldsymbol{r} $$ と表現できる。これに加えて、 $ \boldsymbol{t} = \begin{pmatrix} T_x \\ T_y \\ T_z \\ \end{pmatrix} $ だけ並行移動を施す場合は $$ R \, \boldsymbol{r} + \boldsymbol{t} = \begin{pmatrix} R_{xx} x + R_{xy} y + R_{xz} z + T_x \\ R_{yx} x + R_{yy} y + R_{yz} z + T_x \\ R_{zx} x + R_{zy} y + R_{zz} z + T_x \\ \end{pmatrix} $$ とすればよい(ここで$R_{\cdot\cdot}$は$R$の要素)。
基本的な座標変換には、回転、伸縮や変形、移動があるが、これらをひとつの行列として表現すると色々と都合がよい。 そこで、4番目の座標成分を加えて、ベクトルを$\boldsymbol{s} = \begin{pmatrix} x \\ y \\ z \\ w \\ \end{pmatrix} $ 、変換行列を $$ S = \begin{pmatrix} R_{xx} & R_{xy} & R_{xz} & T_x \\ R_{yx} & R_{yy} & R_{xz} & T_y \\ R_{zx} & R_{zx} & R_{zz} & T_z \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} $$ と再定義しなおせば、$w=1$と置くことで、 $$ \begin{pmatrix} R_{xx} & R_{xy} & R_{xz} & T_x \\ R_{yx} & R_{yy} & R_{xz} & T_y \\ R_{zx} & R_{zx} & R_{zz} & T_z \\ 0 & 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} x \\ y \\ z \\ 1 \\ \end{pmatrix} = \begin{pmatrix} R_{xx} x + R_{xy} y + R_{xz} z + T_x \\ R_{yx} x + R_{yy} y + R_{yz} z + T_x \\ R_{zx} x + R_{zy} y + R_{zz} z + T_x \\ 1 \\ \end{pmatrix} $$ のように、回転や変形と移動をまとめて表現することができる。 このように、$w$を含めた4つの座標で物体等の状態を表現する方法を同次座標系、 その変換を表す4行4列の行列を同次変換行列と呼んでいる。
次に、同次変換行列を使った物体の頂点座標の変換の流れについて見ておこう。
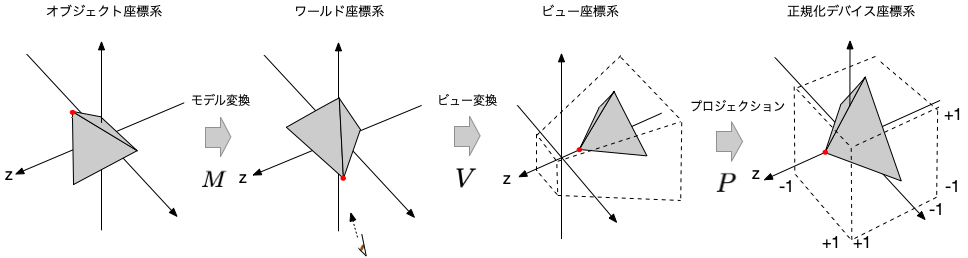
まず、物体のモデリングで用いた座標を、その物体を配置したい位置や向きに応じて変換する(モデル変換)。 次に、設定した視点からそれを眺めた画像を生成するために、視点を中心とした座標に変換する(ビュー変換)。 さらに、投影する範囲と形状を、正規化デバイス座標系(x,y,zのそれぞれが-1から1の範囲の立方体領域)にフィットするような変形を加える(プロジェクション変換)。 それぞれの変換を表す同次変換行列を、$M$, $V$, $P$ とすれば、モデリングで用いた座標(ベクトル)$\boldsymbol{r}$は、これの行列の積を用いて $$ \boldsymbol{r}' = P \, V \, M \, \boldsymbol{r} $$ に変換されることになる(ここで、積の順序に注意)。特に $V \, M$ をまとめて、モデルビュー変換と呼ぶ。
Pygletに用意されている基本的な行列
すでに例題で登場しているとおり、pyglet.math.Mat4クラスには、いくつかの基本的な変換行列が用意されている:
Mat4() ・・・ パラメータ無しのコンストラクターは4×4の単位行列 Mat4.from_translation(Vec3(x方向変位, y方向変位, z方向変位)) ・・・並進移動 Mat4.from_rotation(角度, Vec3(回転軸のx成分, 回転軸のy成分, 回転軸のz成分)) ・・・回転 Mat4.from_scale(Vec3(x方向の拡大率, y方向の拡大率, z方向の拡大率)) ・・・拡大・縮小 Mat4.orthogonal_projection(left, right, bottom, top, z_near, z_far) ・・・ 直交投影行列 Mat4.perspective_projection(aspect, z_near, z_far, fov) ・・・ 透視投影行列

6.2 データの流れ
では、正四面体の表示プログラムを例に、シェーダーの動作についてもう少し詳しく見ていこう。
シェーダープログラムは専用のプログラミング言語であるGLSL(OpenGL Shading Language)で記述されている。 GLSLはC言語に似ているが、基本的には別物と考えたほうがよい。 その仕様については一旦置いておいて、まず、Pythonプログラムとシェーダーとのデータの流れに注目したい。
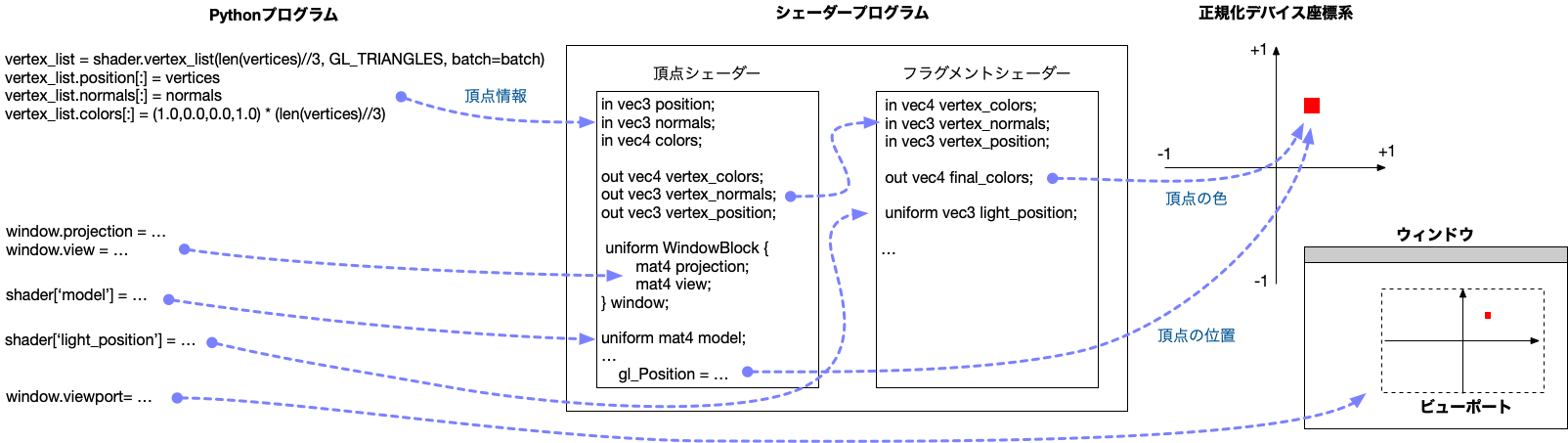
Pythonのプログラムは、ビューポートの設定、プロジェクションやモデル変換行列、図形の頂点座標、法線ベクトル、頂点の色情報など、様々なデータをシェーダー側に送る。 それを受け取ったシェーダーは、GPUを使って座標変換などの処理を行い、その結果を描画デバイスに送り、それが画像として表示されるという流れになる。 PythonコードとGLSLで書かれたシェーダープログラム、そしてウィンドウ表示までのデータの流れを図にまとめた。
通常、OpenGLでシェーダーを使う場合は、VBO(Vertex Buffer Object)と呼ばれるバッファーを介してCPUからGPUにデータを転送する。 データの形式は様々であるので、VBOを使ってやりとりしたい内容について追加的な情報をVAO(Vertex Array Object)として用意する必要がある。 言い換えると、VAOはVBOと連動するデータカタログのようなものである。 ただ、VBOとVAOを適切に管理するのはかなり面倒なので、pygletではこれらを意識せずとも、シェーダーにデータを渡せるような手段(pyglet.graphics.shader.ShaderProgram.vertex_list()等)が提供されている。
現在のバージョンのPygletでは、vertex_list()関数を使って頂点シェーダーに渡すことができる頂点リストはfloat型(またはそのベクトル)のみである。
座標や色情報は実数値として扱うので、通常の使用では特に問題は生じないが、
int型の頂点データを渡したい場合は、OpenGLの関数を直接呼び出してVBOを作成する必要がある。
Pygletのvertex_list()は使わず、VBOでデータを受け渡すコードの例が prog-5-3-vbo.py からダウンロードできるので参照のこと。
GLSLには、座標変換等の計算に便利なデータ型が用意されている。vec2は2次元、vec3は3次元、vec4は4次元のベクトル。
mat3は3×3の行列、mat4は4×4の行列、といった具合である。
また、inで始まる変数はデータ入力、outは出力用であることを示し、
uniformはCPU側からデータを受け取るための専用の領域を表す。
uniform変数は読み取り専用で、シェーダープログラムの中で変更することはできない。
さらに、GLSLにはいくつかの組み込み変数が定義されていて、変数宣言無しに使用できる。gl_Positionが代表的な例である。
gl_Positionは正規化デバイス座標系での頂点座標(同次座標系)を指定するために用いる。
pyglet.graphics.vertex_list()関数は、頂点シェーダに渡すためのお膳立てをしてくれるオブジェクトを生成し、
それを介してinと修飾された変数に頂点データのリストを自動的に受け渡すことができる。
一方、シェーダーのuniform変数は、Python側から
シェーダープログラム名['uniform変数名']
によってアクセスすることができるようになっている。
プロジェクション変換行列とビュー変換行列については、pygletのWindowオブジェクトを介して設定するような仕様になっている。具体的には、pygletが使用する頂点シェーダーでは
uniform WindowBlock {
mat4 projection;
mat4 view;
} window;
というuniform blockを定義するようになっていて、複数のシェーダープログラムが共存する状況でも、プロジェクションとビュー変換を矛盾なく一括で行えるようにしている。 従って、独自のシェーダーを設計する場合でも、この流儀に従っておくのが良いだろう。
頂点シェーダーのout変数は、シェーダーのパイプライン処理によって、フラグメントシェーダーのin変数に渡される。 そのため、頂点シェーダーのout変数とフラグメントシェーダーのin変数は必ず対応していなければならない。 フラグメントシェーダーの出力(out変数)によって、頂点の描画色が決められる。

6.3 頂点シェーダーの動作
まず頂点シェーダーから処理の内容をみていこう。C言語と同様、main()が実行される。
モデルの頂点の3次元座標は変数positionで与えられているので、vec4(position, 1.0)
によって$w=1$であるような同次座標表現に変換する。
その上で、モデル行列とビュー行列を作用させ、新しい座標posに変換するのが
mat4 modelview = window.view * model; vec4 pos = modelview * vec4(position, 1.0);
の部分である。それにさらにプロジェクション行列を作用させ、正規化デバイス座標をgl_Positionに設定しているが、次の行
gl_Position = window.projection * pos;
である。
ある頂点の法線ベクトルを$\boldsymbol{n}$としたとき、モデルビュー変換を施した後に、法線はどのように変換されるだろうか。 面を構成するベクトル(面に平行な任意のベクトル)を $\boldsymbol{v}$ とすると、法線の定義から、$\boldsymbol{n} \cdot \boldsymbol{v}= 0$ が必ず成り立つ。 法線の方向は並行移動によっては変化しないので、回転や変形操作のみが問題となる。 回転や変形を表す行列を$M$とすると、面を構成するベクトルは$\boldsymbol{v}' = M \boldsymbol{v}$ のように変換されることになる。 一方で、法線の変換が行列$R$で表されると仮定すると(すなわち $\boldsymbol{n}' = R \boldsymbol{n}$)、変換後にも法線と面を構成するベクトルは直交していなければならないので、 $$ \boldsymbol{n}' \cdot \boldsymbol{v}' = R \boldsymbol{n} \cdot M \boldsymbol{v} = \left(R \boldsymbol{n}\right)^\top M \boldsymbol{v} = \boldsymbol{n}^\top \left( R^\top M \right) \boldsymbol{v} = 0 $$ が、全ての面について、法線$\boldsymbol{n}$とその面に並行な$\boldsymbol{v}$の組で成り立たなければならない。 明らかに $$ R^\top M = I $$ ($I$は単位行列)が成り立っていれば $\boldsymbol{n}^\top I \boldsymbol{v}=\boldsymbol{n} \cdot \boldsymbol{v}=0$であり、$\boldsymbol{n}'$ が $\boldsymbol{v}'$と直交することが保証される。従って、 $$ R= \left( M^{-1} \right)^\top $$ すなわち、モデル変換行列の回転や変形を表す部分の逆行列の転置によって法線は変換すれば良い($M$が回転のみの操作であれば$R=M$)。 この変換行列を求めているのが、
mat3 normal_matrix = transpose(inverse(mat3(model)));
である。さらに、ビュー変換後の頂点の座標、頂点の色、そしてモデルビュー変換後の法線ベクトル
vertex_position = pos.xyz; vertex_colors = colors; vertex_normals = normal_matrix * normals;
によってフラグメントシェーダーに引き次いでいる。

6.4 フラグメントシェーダーの動作
フラグメントシェーダーのmain()関数では、頂点シェーダーから渡された法線ベクトルの長さを1に規格化し
vec3 normal = normalize(vertex_normals);
頂点から相対的に眺めた光源への方向ベクトルを求め、それを規格化する。
ここでは、光源の位置 light_position はビュー座標で指定すること(「観察者」がライトを持っているような状況)を想定している点に注意。
vec3 light_dir = normalize(light_position - vertex_position);
法線ベクトルと光源の方向ベクトルとの内積を計算し、0以下であれば0として、光の散乱の量diffを算出する。
これは『表面の単位面積あたりに入射する光のエネルギーによってその面の明るさは決まるだろう』というモデル化(単純化)である。
float diff = max(dot(normal, light_dir), 0.0);
最後に、頂点の色に散乱の量を乗じることで、その面からの色とその強度としている:
final_colors = vertex_colors * diff * 1.2;
ここで、1.2を乗じているのは、面をやや明るめに表現するためである。
GLSLについてのより詳細な情報源
ここまでは、データの受け渡しと処理の流れを中心に説明したため、シェダープログラムの細かい機能についてはスキップしてきた。 GLSLは誕生から幾度も改定され、新しい機能が追加されて来た。 この解説で主に使用しているのは、ほとんどのパソコンで動作すると思われるバージョン3.30である。
GLSLについてさらに詳しくは、以下のサイトや文書を参照すると良い。
- Rendering Pipeline Overview(Wiki)
- The OpenGL Shading Language(PDF)
- yphoonLabs' OpenGL Shading Language tutorials