Pythonプログラミング（総合演習・図形の描画）

準備

まず、以下の準備を行なっておく：

1. TurtleEditの「実行」メニューの中から「設定」を選び、「亀場を自動起動」にチェックを入れておく。
2. turtle3.pyをダウンロードして、プログラミング作業用のフォルダに保存・移動する。

TurtleEditと亀場使い方についてはこちらのページも併せて参照のこと。

動作の確認

ダウンロードと解凍が完了したら、以下の手順で、動作確認を行う：

まず、亀場の解説の、タートルグラフィックスとは、と、 亀場の様子についての記述を読んでおく。

次いで、以下のサンプルコードをエディタのコピーし、ファイルに保存する(square.py)。保存先のフォルダーに、 先ほどダウンロードした turtle3.py (Python 2 の場合は turtle.py）があることを確認する。

from turtle3 import Turtle

ttl = Turtle("localhost")

ttl.clr()
ttl.rst()
ttl.pd()
ttl.fd(100)
ttl.lt(90)
ttl.fd(100)
ttl.lt(90)
ttl.fd(100)
ttl.lt(90)
ttl.fd(100)

これを実行し、亀場に赤い四角形が表示されることを確認する。

Pythonの関数を使って、図形を部品化する

亀場で練習：基本図形の描画を関数にまとめる

以下は、亀場に１辺の長さが100の六角形を描くプログラムの例である。

# coding:utf-8
from turtle3 import Turtle

t=Turtle("localhost") # 亀場と接続 
t.clr() # 画面をクリア
t.rst() # 亀を中央・右向きにリセット 
t.pd()  # ペンを下ろす 
for i in range(6):
   t.fd(100) # 100前進 
   t.lt(60)  # 左に60度回転 
t.pu()  # ペンを上げる

このプログラムを発展させて、亀場 t に、一辺の長さが s の6角形を座標 (x,y) を出発点にして描く関数 hexagon(t, x, y, s) を設計し、動作を確認せよ。以下をひな形とするとよい：

# coding:utf-8
from turtle3 import Turtle

def hexagon(t, x, y, s):
  ?????	

# メイン部
t=Turtle("localhost") # 亀場と接続 
t.clr() # 画面をクリア
hexagon(t,0,0,50) # 関数の呼び出し

　ヒント

亀を座標(x,y)に移動させるには、jump(x,y) メソッドを呼び出せばよい。 また、亀の方向を右向き（角度０）にリセットするために east() メソッドが使える。

亀場で練習：六角形がいっぱい

上記プログラムをさらに手直しして、下図のように、六角形を縦横に並べて描画しなさい。

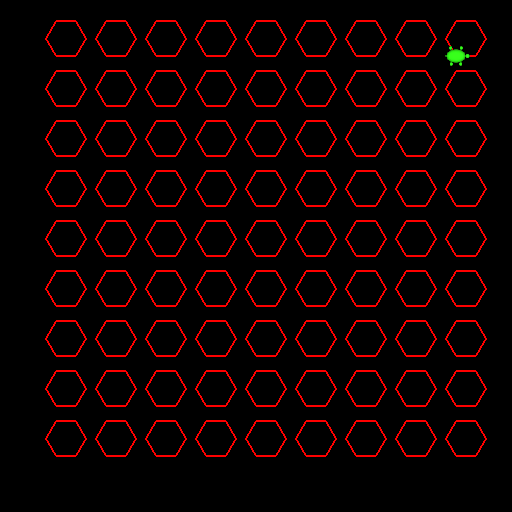
　ヒント：塗りつぶし

関数定義のところを

def hexagon(t, x, y, s) :
   t.jump(x,y)
   t.east()
   t.fill() # この行を追加
   t.pd()
   ....

と変更すると、四角形の領域が塗りつぶされる。

　スクリーンショットの撮り（取り）方

課題では、プログラム（何々.py）に加えて、亀場のスクリーンショットの提出が求められる。スクリーンショットを取る方法は以下のとおり：

1. 亀場に図形などが表示されている状態で、亀場のウィンドウのどこかをクリックして、前面に出す
2. その状態でキーボードの p キーを押す
3. ホームディレクトリ（デスクトップではない）に tfield-capture-xxxxx.png という画像ファイルが作成されているので、適宜、名前を変更する

図形の位置をさらに緻密に制御する

まず、タートルグラフィックスの解説のページの「亀で描く基本的な図形」の「正Ｎ角形」の解説をよく読んでおく。

上記の解説に書かれているとおり、正三角形の場合、半径200の円に内接する正三角形の辺の長さ$s$は $$ s = 2 \times 200 \sin\left( \frac{2 \pi}{2 \times 3} \right) = 2 \times 200 \sin\left( \frac{\pi}{3} \right) $$ である。これをPython風に書けば s = 2*200*math.sin(math.pi/3) ; となる。

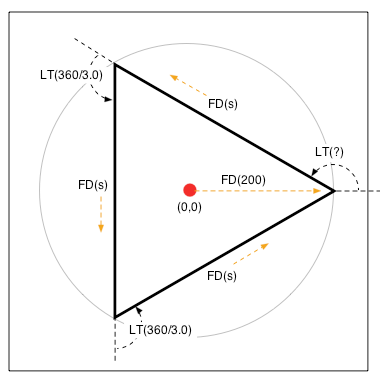
原点を中心とした半径200の円に内接する正三角形を描くには、まず、ひとつ目の頂点に移動しておく必要がある。そのためには

t.jump(0,0) # 原点に移動する 
t.east()    # 右横方向に向きを整える 
t.fd(200)   # 200前進する 

すれば良い。

その後、「しかるべき」角度だけ左回転した後、ペンを下ろし、

t.fd(s)  # sだけ前進 
t.lt(360.0/3)  # 120°左回転

を三回繰り返せば、所望の三角形が描けるはずだ（下図を参照）。

ここまでの流れをプログラムにまとめると、以下のようになる：

# coding: utf-8
import math
from turtle3 import Turtle

    
t = Turlte("localhost")
t.clr()
t.jump(0,0)
t.east()
t.fd(200)
t.lt(ある角度); # ここを考える

s = 2*200*math.sin(math.pi/3) 
	
t.pd()
for i in range(3):
    t.fd(s)
    t.lt(360.0/3)

t.pu()

亀場で練習：円に内接する正三角形および正N角形

上記プログラムの「ある角度」の箇所を適切に設定し、動作を確認しなさい。

うまく動いたら、さらに、線の色や太さなども調整してみなさい。

この例では「右向き」の頂点から描画を始めているが、それを「上向き」からに変更してみなさい。

正N角形のNを表す変数を用意し、その変数の値（3,4,5...)に応じてN角形が描けるように拡張しなさい。