亀場でプログラミング:タートル・グラフィックス
このページでは、タートルグラフィックスを使って、幾何学的な図形を描くことに挑戦する。
1. 亀で描く基本的な図形
「直進と後退」、「回転」、そして「ペンダウン」、「ペンアップ」の組み合わせだけで、どれくらいマシな図形が描けるものだろうか。 そこでまず、「原点(0,0)を中心とし、半径rの円に内接する正N角形」から始めてみよう。
正N角形
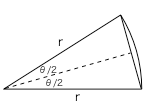
二辺の長さがrで、その間の角度が$\theta = 2\pi/N$であるような二等辺三角形を考えると、いま考えている正N角形の1辺の長さは、その二等辺三角形のもうひとつの辺の長さ($s$としよう)に等しいことは明らか。そこで、ちょっと考えれば $$s = 2 r \sin\left(\frac{\theta}{2}\right)$$ である(余弦定理を使うまでもない・・・)。
こうして、長さsだけ前進する度に、角度 $\theta = 2 \pi/N$だけ決まった方向に回転し、再びsだけ前進、をN回繰り返せば、正N角形を描くことができるはずだ。
 練習:正五角形の描画
練習:正五角形の描画
原点(ウィンドウの中央)を中心とし、r=100 の正5角形を描くプログラムを作り、動作を確認しなさい。
 ヒント
ヒント
#include <math.h>しておくと, M_PIという記号には円周率の値(3.141592...)がセットされる。
上の説明では、角度は弧度法(ラジアン)を使った。一方、タートルグラフィックスでは度数法(°)を用いる。aラジアンの角度を度数法に変換するには、180.0*a/M_PIとすればよい(M_PIは円周率を表す)。
関数RST();を呼び出した後、亀は原点(0,0)で右向きの状態にある。それを5角形の辺の上に移動させて(角度も整えて)から描画を開始しないと、ウィンドウ上での位置がずれてしまう。
念のために、ひな形を示しておく:
#include <stdio.h>
#include <math.h>
#include "turtle.h"
main( )
{
int n,i ;
float s,dt ;
CON("localhost") ;
CLR() ;
RST() ;
COL(1.0,1.0,0.0) ; /* 描画色を黄色に変更する例 */
・・・
for (n=0; n<5; n=n+1) {
・・・
}
・・・
}
円
正N角形のNを大きくすれば、それは円になる。一方、十分Nが大きければ、$\theta$は小さい数になるから、正弦関数を0の周りでテイラー展開して $$\sin\left(\frac{\theta}{2}\right) = \frac{\theta}{2} + \cdots$$ sの式に代入すると、 $$s = r \,\theta$$ となる(要するに、三角形の辺の長さを円弧のそれで近似しただけ)。
こうして、三角関数を用いなくても円が描画できることが解った。
 練習:円の描画
練習:円の描画
原点(ウィンドウの中央)を中心とし、r=100 の円を描画するプログラムを作りなさい。プログラム中で三角関数は使わないこと。
 解説
解説
亀が$\Delta s$だけ進む間に(弧度法で)角度$\Delta \theta$だけ回転したとすると、その比率$\frac{\Delta \theta}{\Delta s}$ を曲線の曲率(curvature)と呼ぶ。 この定義を使えば、「円は曲率が一定であるような曲線」と言い換えることができる。 曲率を$\kappa$とすると、その逆数$1/\kappa$は、曲線のその部分にちょうどフィットする円の半径に相当しており、曲率半径と呼ぶ。 上の式を思い出すと、円の曲率半径は確かに $\frac{\Delta s}{\Delta \theta} = r$ となっている。
一般の曲線は場所毎に曲率が異なる。言い換えると、進んだ距離に応じて回転角を調整することで、さまざまな種類の曲線を描くことができるわけだ。
 発展:対数螺旋
発展:対数螺旋
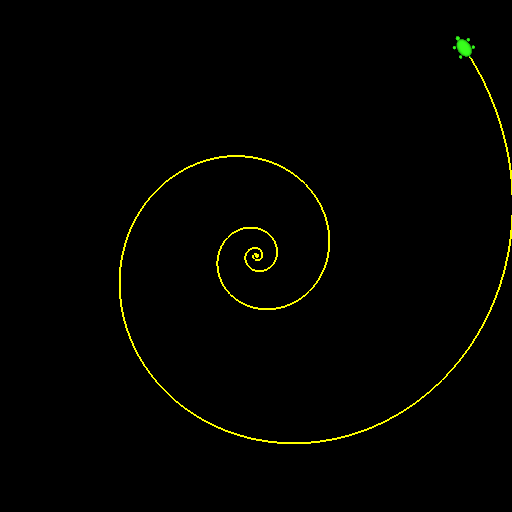
対数螺旋(logarithmic spiral)は、生物の形態などとも関係して、色々な文脈で現れる曲線である。 対数螺旋を極座標 $(r,\theta)$ で表現すると、2つのパラメータ $a,b$ を使って $$ r = a e^{b \theta} $$ となる ( $x(\theta) = a e^{b\theta} \cos\theta$, $y(\theta) = a e^{b \theta} \sin \theta$ )。
対数螺旋の曲率を道のりの関数として求め、それを用いて、亀場に対数螺旋を描いてみなさい。
 ヒント
ヒント
描き始めの角度が $\theta_0$ だったとすると、ぐるぐる回って $\theta$ に至るまでの道のりは $$ s(\theta) = \int_{\theta_0}^\theta \sqrt{\left(\frac{dx(\theta)}{d\theta}\right)^2 + \left(\frac{dy(\theta)}{d\theta}\right)^2} \,\,d\theta = \frac{a\sqrt{1+b^2}}{b}\left(e^{b\theta} - e^{b\theta_0} \right) $$
この式から、曲率 $\frac{d \theta}{d s}$ を歩いた距離($s$)の関数として求め、$s$ に応じて向きを調整すればよい。
1ピクセルを長さ1としたとき、$a=0.1, b=0.2, \theta_0=0$ とおいて描いた螺旋の例
 発展:8の字
発展:8の字
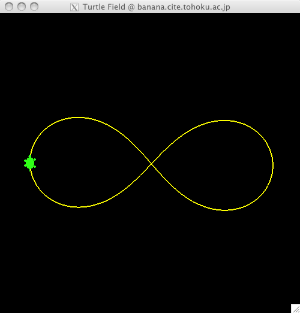
亀が進む毎に回転角を変化させなければならない例として、横に寝た8の字(∞の記号)を描いてみよう。 下図のように亀に8の字を描いて歩かせ、(できるだけ)元の位置に戻ってくるようプログラムしなさい。
各ステップでのx,y方向の変位の総和を計算すれば良い。
TPRINTF( )関数を使って(コンソールではなく)亀場に数値をプリントすることもできる。
その際、きちんと戻って来たか確かめるために、出発地点を基準(0,0)とした場合、終点の相対座標がどうなっているのかを、printf()関数を使ってプリントすること。
 ヒント
ヒント
例えばあなたが自転車に乗って8文字走行する場合、ハンドルをどのように切ればよいか、想像してみよう。 ハンドルの切れ角が$\Delta \theta$に比例すると考えればよさそうだ (右にハンドルを切ると$\Delta \theta$はマイナス、左だとプラス)。
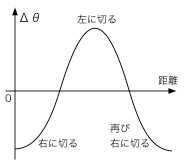
図で亀のいる位置から上方向に出発したとしよう。 すると、あなたは最初に右にハンドルを切った状態からはじめて、中央のクロスしているところで、今度は 左にハンドルの向きを変え、そのままターンして、再び中央にさしかかったら、今度はハンドルを右に戻す。 そしてしばらく走ると、元の場所(図の亀の位置)に戻ってくるはずだ。
そんなハンドルの切り方をさせる一案として、 8の字を一周するのに$N$ステップを要するとすると(いつも歩幅は等しいと仮定すれば)、$k$ステップ目の ハンドルの角度を $$ \Delta \theta(k) = -A \cos( 2\,\pi\,k\,/\,N ) $$ とすれば良さそうな気がする。ただし、ここで$A$はある正の数。
$A$の求め方は高校レベルの数学をちょっと越えるので、 ガッツのある諸君のために、別のページにアウトラインだけ紹介しておいた。 その答えは $$ A = 2.40482 \times 360\, / \,N \;\; \textrm{[degree]} $$ となる。
2. 反復を使って描くことができるさまざまな図形
比較的単純な操作のみで描くことができる図形の例を示したので、是非挑戦してみてほしい。
また、ネットで 〔turtle graphics example〕をキーワードに画像検索してみると、さまざまな面白い例が見つかるはずだ。
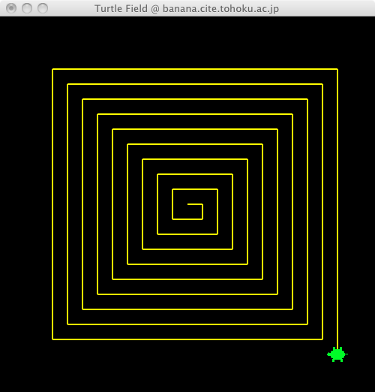
スパイラル
中心から右向きに出発したとして、どのような描画パターン(線の長さ、転回角度)の繰り返しになっているのかをまず考える。
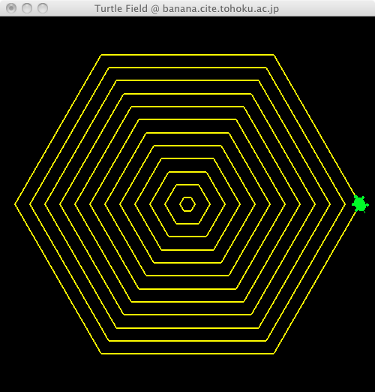
蜘蛛の巣状の六角形
すでに正N角形の描き方は習得済み。内接円のサイズを変えながら、複数回、六角形を描けばよい。
描画を始める際の亀の向きを整えることと、
ペンの上げ下げ(PU(),PD())、座標のリセット(HOME())を適切なタイミングで使うのがミソ。
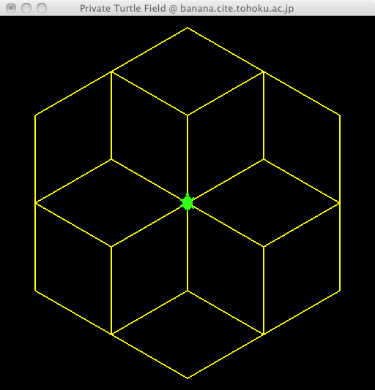
重なった六角形
色々な描き方があるとは思うが、同じ大きさの六角形を6つ重ねるのが簡単そうだ。
その場合、二度描きされる線分が何カ所もある(が、見かけは1本の線になる)。
ついでながら、右の図形は、ネッカーの立方体
のようなだまし絵にもなっている。じっと見ていると、凹凸の関係が、ときどき反転して見えませんか?
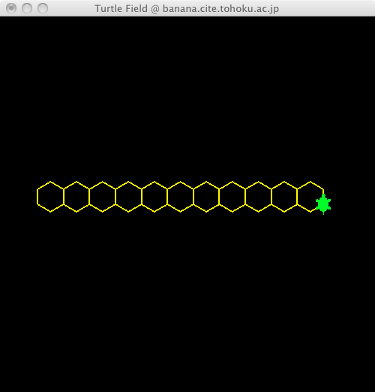
六角形のチェイン
「六角形を描いて、ペンを上げ、横に移動し、ペンを下ろし、また六角形を描く」の繰り返しで何とかなりそうだ。
六角格子
六角形のチェインを縦方向にずらしながら並べれば良さそうだが、少々面倒(工夫が要る)かもしれない。
1種類の正多角形で平面を隙間無く埋め尽くすために使うことのできる「ピース」は、正三角形、正方形、そして、この正六角形のみ。
平面の充填の問題は、
物理学、工学、デザインや芸術など、諸々の事象に関係していて、とても興味深い。
