サンプルプログラム集 (Python)

このページでは、「亀場」を使ったサンプルコードをいくつか紹介します。 プログラムの実行には亀場サーバーが必要です。 turtle3.py をダウンロードの上、下記のサンプルコードと同じディレクトリ（フォルダ）に保存しておいてください。

Python 2をお使いの場合は turtle.py をダウンロードの上、 コードの冒頭の from turtle3 import Turtle の箇所を from turtle import Turtle と書き換える必要があります。

Pythonに不慣れな方は Pythonで学ぶコンピュテーショナル・シンキング もご覧ください。

フラクタル曲線

ヒルベルト曲線(Hilbert curve)を描くサンプルプログラム。描画が終わると、ロボット亀が登場するはず。
tfield-examples-hilbert-small 
from turtle3 import Turtle

STEP=13.0

def hilbert(level, angle):
	if level<=0:
		return
	ttl.rt(angle)
	hilbert(level-1,-angle)
	ttl.fd(STEP)
	ttl.lt(angle)
	hilbert(level-1,angle)
	ttl.fd(STEP)
	hilbert(level-1,angle)
	ttl.lt(angle)
	ttl.fd(STEP)
	hilbert(level-1,-angle)
	ttl.rt(angle)

ttl = Turtle("localhost")
ttl.clr()
ttl.rst()
ttl.lw(2)
ttl.col(1.0,1.0,0.0)
ttl.bk(200)
ttl.lt(90)
ttl.fd(200)
ttl.rt(90)
ttl.pd()
hilbert(5,90.0)
ttl.fire()
ttl.robot()

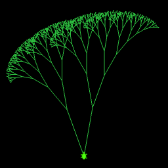
「ツリー」の描画

再帰を使って、樹形の様なパターンを描くプログラム。亀が行きつ戻りつしている様子が観察できます。
tfield-examples-tree-small 
from turtle3 import Turtle
ttl=Turtle("localhost")

def branch(step):
	if step<4.0:
		return
	else:
		ttl.lt(20)
		ttl.pd() ; ttl.fd(step) ; ttl.pu()
		branch(step*0.6) ;
		ttl.bk(step)
		ttl.rt(20)

		ttl.rt(10)
		ttl.pd() ; ttl.fd(step) ; ttl.pu() ;
		branch(step*0.7)
		ttl.bk(step)
		ttl.lt(10)


ttl.clr()
ttl.rst()
ttl.col(0.1,0.7,0.2)
ttl.jump(0,-220)
ttl.north()
branch(150)

シェルピンスキーのガスケット

これも代表的なフラクタル図形。FILLモードを使っている。
tfield-examples-sierpinski-small 
from turtle3 import Turtle
ttl = Turtle("localhost")

def triangle(size):
	ttl.fill(); ttl.pd(); ttl.fd(size)
	ttl.lt(120); ttl.fd(size); ttl.lt(120)
	ttl.fd(size); ttl.pu(); ttl.lt(120)

def sierpinski(size):
	if size<20.0:
		triangle(size)
		return
	else:
		sierpinski(size/2.0)
		ttl.fd(size/2.0)
		sierpinski(size/2.0)
		ttl.lt(120)
		ttl.fd(size/2.0)
		ttl.rt(120)
		sierpinski(size/2.0)
		ttl.rt(120)
		ttl.fd(size/2.0)
		ttl.lt(120)

ttl.clr()
ttl.jump(-250,-200)
ttl.east()
sierpinski(500)

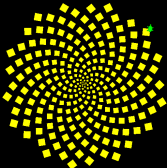
ひまわり

右回りと左まわりの螺旋が「見える」だろうか。

tfield-examples-sunflower 
import math
from turtle3 import Turtle
ttl=Turtle("localhost")

def seed(x, y, size):
	step=size*math.sqrt(2.0)
	ttl.jump(x,y)
	ttl.east() ;
	ttl.lt(math.atan2(y,x)*180.0/math.pi)
	ttl.fd(size)
	ttl.lt(135)
	ttl.pd()
	ttl.fd(step); ttl.lt(90); ttl.fd(step)
	ttl.lt(90); ttl.fd(step); ttl.lt(90); ttl.fd(step)
	ttl.pu()

GR=(1.0+math.sqrt(5.0))*0.5 
ttl.clr()
ttl.fill()
ttl.col(1,1,0)
for n in range(1,250):
	x = n*math.cos(2*math.pi/(GR*GR)*n)
	y = n*math.sin(2*math.pi/(GR*GR)*n)
	seed(x,y,math.sqrt(n))

書道

「亀」と書くプログラム。Pythonのプログラムとしては全く見所はありませんが、BRUSHモードを使った例として。
tfield-examples-brush-kame-small 
from turtle3 import Turtle

t = Turtle("localhost")
t.rst()
t.bgc(0.8,0.8,0.7)
t.clr()
t.col(0,0,0) ;
t.brush()
t.lw(30)
t.jump(10,205)
t.west(); t.lt(40) ; t.pd() ; t.fd(100) ; t.pu()
t.jump(0,190) ; t.east() ; t.rt(30) ; t.pd() ; t.fd(40) ; t.rt(120) ; t.fd(100) ; t.pu()
t.jump(-90,120) ; t.east() ; t.lt(5) ; 
t.pd() ; t.fd(170) ; t.rt(100) ; t.fd(80) ; t.fd(0) ; t.pu()
t.jump(-90, 100) ; t.south() ; t.lt(8) ; t.pd() ; t.fd(60) ; t.fd(0) ; t.pu() 
t.jump(-70, 80) ; t.east() ; t.lt(5) ; t.pd() ; t.fd(130) ; t.fd(0) ; t.pu()
t.jump(-70, 40) ; t.east() ; t.lt(5) ; t.pd() ; t.fd(130) ; t.fd(0) ; t.pu()
t.jump(-130,0) ; t.east() ; t.lt(5) ; t.pd() ; t.fd(250) ; t.rt(100) ; t.fd(90) ; t.fd(0) ; t.pu()
t.jump(-120, -5) ; t.south() ; t.lt(8) ; t.pd() ; t.fd(80) ; t.fd(0) ; t.pu()
t.jump(-100, -40) ; t.east() ; t.lt(5) ; t.pd() ; t.fd(200) ; t.fd(0) ; t.pu()
t.jump(-110, -80) ; t.east() ; t.lt(5) ; t.pd() ; t.fd(220) ; t.fd(0) ; t.pu()
t.lw(35)
t.jump(0,110) ; t.south(); t.rt(5)
t.pd() ; t.fd(210)
for cnt in range(10):
	t.lt(10) ; t.fd(8)
t.fd(120) ; t.lt(85) ; t.fd(50) ; t.pu()

雲のようなパターン

自己アフィンフラクタル（的）なパターンを生成する例。 少しリストが長くなるので、以下にリンクを設けました。 これと同様の手法が、コンピュータグラフィックスで地形や雲を生成する際に使われています。

Pythonコード (cloud4.py)

tfield-examples-cloud4

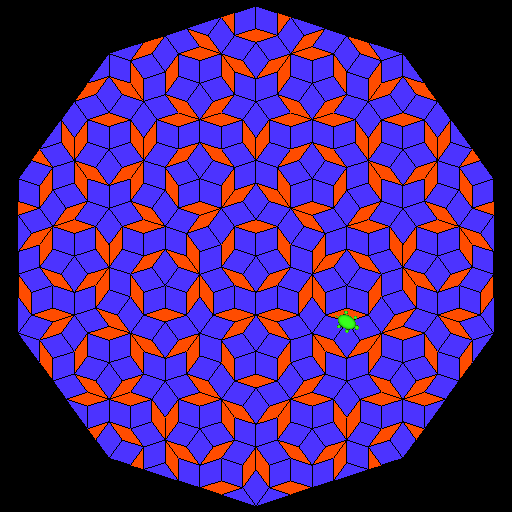
ペンローズ・タイリング

二種類のタイルで非（準）周期的に空間を充填するペンローズ・タイリングの例。

Pythonコード (penrose-tile.py)

images/penrose-tile

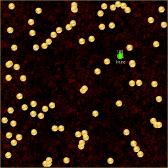
掃除ロボット

亀場にコインを100枚ばらまいてから、カメがそれを回収します。 プログラムを複数走らせることによって、複数のカメが共同でお掃除してくれます。
tfield-examples-cleaning-small 
from turtle3 import Turtle 

class Sweeper(Turtle):
	def run_into_wall(self,tm):
		for cnt in range(60):
			self.lt(3)
	def run_into_turtle(self,tm):
		for cnt in range(40):
			self.lt(3)
	def found_coin(self,tm):
		self.pickcoin()

s = Sweeper("localhost")
s.bmode()
s.nm("kame")

if s.q_nt()==1:
	for cnt in range(100):
		s.coin()

while True:
	s.fd(2)
	s.rt(0.2)

コイン集め

上の例と同様に、コインを100枚散らかしてから、「コインが見つかったときに、もしコインを持っていたらその場に落とす、 持っていなければ拾う」を繰り返す例です。 ここで、「コインが見つかる」とは、「周囲にコインが無い状態からある状態に変化した」という事象のことです。 プログラムを走らせているうちに、（効率は悪いですが）だんだんとコインが集まっていく様子が観察できるはずです。

この例では、スレッドを使って、10匹の亀が同時にコイン集めをしてくれます。
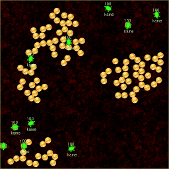
tfield-examples-coin-move-small

10匹の亀が同時にコイン集めをしている例

from turtle3 import Turtle
import threading

class Collector(Turtle):
	def run_into_wall(self,tm):
		for cnt in range(50):
			self.lt(3)
	def run_into_turtle(self,tm):
		for cnt in range(50):
			self.lt(3)
	def found_coin(self,tm):
		nc = self.q_mycoin()
		if nc>0:
			self.dropcoin()
		else:
			self.pickcoin()

def walk_about(t):
	while True:
		t.fd(2)
		t.rt(0.2)
						
n = 10
threads = []
for i in range(n):
	t = Collector("localhost")
	t.bmode()
	t.nm("kame"+str(i))

	if t.q_nt()==1:
		for cnt in range(100):
			t.coin()
	thrd = threading.Thread(target=walk_about,args=(t,))
	threads.append(thrd)
	thrd.start()

for thrd in threads:
	thrd.join()

ハノイのカード

よく知られた「ハノイの塔」をトランプのカードを使って表示するデモ。 動作には、2017年6月版以降のバージョンの亀場サーバーとturtle.pyが必要。

tfield-examples-card-hanoi

トランプによる「ハノイの塔」

from turtle3 import Turtle

ttl=Turtle("localhost")

card=[[0 for i in range(53)] for j in range(3)] 
ncard=[0,0,0]

def redraw(x):
	ttl.clr()
	for i in range(3):
		for j in range(ncard[i]):
			k = card[i][j]
			ttl.card(k, -200 + i*150.0 - j*2, -220+j*30.0) 
	ttl.jump(-160 + x*150.0, -140+(ncard[x]-1)*30.0) 

def move_card(x, y):
	if ncard[x]>0:
		ncard[x]-=1
		card[y][ncard[y]] = card[x][ncard[x]]
		ncard[y]+=1
	redraw(y) ;

def move(n, x, y, z):
	if n==2:
		move_card(x,z)
		move_card(x,y)
		move_card(z,y)
	else:
		move(n-1,x,z,y)
		move_card(x,y)
		move(n-1,z,y,x)


n=13
ttl.clr()
ttl.clrcard()
ttl.bgc(0.1, 0.3, 0.1)
ttl.north()
ncard[0]=n
for k in range(n):
	card[0][k] = 39+n-k 

redraw(0)
move(n,0,2,1)