Pythonプログラミング（ステップ８・関数・基本編）

このステップの目標

• 引数の受け渡し、戻り値の処理、関数の中の変数のスコープを意識し、関数の定義と呼び出しの作法のパターンに従って、プログラムを記述できる
• 複雑な処理を、関数を使って複数の要素に分解・構成できる

１．プログラム言語の語彙（動詞）を拡張する

アルゴリズムを記述する際に、例えば、

(a + b)/2.0 の値を計算して c に代入する

と記述する代わりに、もし「相加平均」という語彙を知っていれば、

２つの実数 a,b の相加平均を c に代入する

と書いても構わない。そして、むしろ、後者のほうが処理の内容をより的確に表現していると言えるだろう。

Cの処理系には「2つの実数の相加平均を求める」という機能はもともとは備わっていないが、「関数」という機能を使うと、 こうした「動詞句」（・・・に対して・・・を行なう）という語彙を加えることができる。

相加平均の場合は、プログラム中に

def arithmetic_mean(x,y):
	return (x+y)/2.0

と記述（関数定義）することで、arithmatic_mean(実数,実数)という語彙が追加され、 『aとbの相加平均をcに代入する』は

c = arithmatic_mean(a,b)

と記述できるようになる。

語彙を拡張する例をもうひとつ挙げておこう。バブルソートのアルゴリズム中には

という「動詞句」が登場した。これをPythonの関数として定義すると

# 『リストのi番目とj番目の要素の値を入れ替える』
def swap(list,i,j):
	w = list[i]
	list[i]=list[j]
	list[j]=w

となり、例題9aのコードは、より「すっきり」と、

# coding: utf-8

def swap(list,i,j):
	w = list[i]
	list[i]=list[j]
	list[j]=w

x=[2.1, 5.3, 7.3, 4.7, 9.2, 1.2, 3.1, 5.3, 8.3, 4.8]

for i in range(0,len(x)-1,1):
    for j in range(len(x)-1,i,-1):
        if x[j-1]>x[j]:
            swap(x,j,j-1)

for i in range(0,len(x),1):
    print(x[i])

と書くことができる。

これらの例ではあまり関数の有難味を感じられないかもしれないが、もし語彙に

「２つの整数の最大公約数を求める」
「実数データ列の分散を計算する」
「実数データ列を昇順に並べ替える」
等々

が加わっていれば、アルゴリズムがとても見通しよく実装できる場合があるはずだ（その細かい手順をいちいち指示しなくても良いから）。

詳しくは以下で説明するが、語彙を追加（関数を定義）するには

def 動詞句の名前(「目的語」に相当する変数のリスト):
    動詞句の定義

のパターンをソースコード中に箇条書きにすればよい。

これまでは関数が登場しないプログラムばかり扱ってきたが、 一般にPythonのプログラムは（沢山の）関数の集まりで構成され、 ソースコードの外見は、

# coding: utf-8
import 何々
...

def func():
   何々
   
def proc():
   何々

その他の関数定義が続く・・

プログラムのメイン部

のようになる。 そして、それぞれの関数によって定義された「新しい動詞句」が、プログラムの中で使えるようになる。

ここではその具体的な方法は説明しないが、関数の定義を、いくつものファイルに分散して記述することもできる。

２．関数の呼び出しとデータの受け渡し

以前、ステップ２で、三角形の三辺の長さから、面積を計算するプログラムを作成した。 それをベースに、面積を計算してプリントする箇所を関数にまとめたプログラムの例を以下に示した。 ここで新たに定義しているのはprint_area_of_triangle()という名前の関数で、 『３つの実数を辺の長さとする三角形の面積をプリントする』という動詞句を定義したことになる。

# coding: utf-8
import math

def print_area_of_triangle(a,b,c):
    s = (a+b+c)/2 ;
    print("S=",math.sqrt(s*(s-a)*(s-b)*(s-c)))

# メイン部
x,y,z=map(float,input("三角形の辺の長さ:").split())
print_area_of_triangle(x,y,z)

関数の呼び出し

言葉を定義しても、それを文章で使わななければ意味が無い。 同じように、関数を定義しただけでは、関数は具体的な働きをしてくれない。 関数を実際に働かせるための手続きを関数呼び出し(function call)と呼ぶ。

プログラムを実行すると（TurtleEditの実行ボタンを押すと）、メインの部分に書かれた内容から実行が始まる。 そして、関数名の書かれた箇所にさしかかると、その関数の定義に従って、そちらの関数の内容が順に実行される。 その関数の処理がひととおり終わると、再びその関数を呼び出した箇所の次から、処理が再開される。 この一連の手続きが関数呼び出しである。 例題10aでは、メインパートからprint_area_of_triangle()関数が呼び出されている。

プログラムは、関数が別の関数を呼び出し、その関数がまた別の関数を呼び出して・・・、といった具合に、いわば関数呼び出しの連鎖の形で構成されるのが常であり、 どの関数の中からどの関数（その関数自身も含む）を呼び出しても構わない。

引数（パラメータ）の引渡し

上記の例では、三角形の３つの辺の長さが、関数print_area_of_triangle()に受け渡されている様子がすぐに想像できるだろう。

その一連の動作を、整理しておこう。 関数の定義の冒頭のprint_area_of_triangle(a, b, c)は、以下のふたつの指示を含意している：

• この関数内でのみ使う変数a, b, cを確保する
• これらの変数の初期値は、関数を呼び出す際に、括弧の中の対応する箇所に書いた内容（値）に自動的にセットされる。

この例題の場合、 print_area_of_triangle()関数が呼び出されると、呼び出し側のx,y,zの値が、 呼び出される側の変数a,b,cに代入される。 このように、関数に「受け渡される」データを、関数の引数(ひきすう）と呼ぶ。 こうしたデータの受け渡しは、引数のリストの順番にしたがって行われる。 よって、この例では x→a, y→b, z→cという対応関係になる。

こうした一連の動作を以下に図示したので、上の説明と併せて参照すること：

３．戻り値のある関数

上の例題に手を加えて、呼び出し側に値を戻す関数を使った例を以下に示す。 この例では、関数area_of_triangle()で計算した三角形の面積を、呼び出し側で「受け取って」いる。 この動作は、これまでの演習でも使ったmath.sqrt()やmath.sin()等と同様、 より「関数らしい」動作と言えるかもしれない。

加えて、三角不等式を使って、辺の長さをチェックする関数 can_form_triangle() を、新たな部品として追加し、 面積が計算できないような場合にも対応できるように、プログラムを拡張した。

# coding: utf-8
import math

def can_form_triangle(a,b,c):
    if a+b>c and b+c>a and c+a>b:
        return True
    else:
        return False

def area_of_triangle(a,b,c):
    s = (a+b+c)/2 ;
    return math.sqrt(s*(s-a)*(s-b)*(s-c))

# メイン部
x,y,z=map(float,input("三角形の辺の長さ:").split())
if can_form_triangle(x,y,z):
    area=area_of_triangle(x,y,z)
    print("S=",area)
else:
    print("三角形が構成できません")

計算結果を呼び出し側に「戻す」働きをさせるためには、 関数内の処理の最後にreturn 式 を実行する。 すると式の値が呼び出し側に返される（リターンされる）。 return文は、関数のおしまいに限らず、どこに記述してもよい。

４．ソフトウェアの部品としての関数

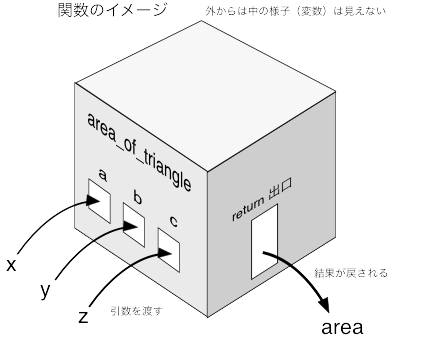
上で述べた例で、関数area_of_triangle( )が働く様子を、呼び出し側から眺めてみたとすると、（講義担当者の頭の中には）下の様な情景が浮かんでくる。

関数の中身はブラックボックスになっていて、中の様子（どんな処理が行われていて、どんな変数が使われているか）はのぞき見ることができない。 ただ、引数に対応する「受付」の窓口があって、そこにデータを渡すと、 処理の結果出てきた別のデータ（return 式によって返されてくる戻り値）を受け取ることが、呼び出す側の処理の全てだ。 そのあとで、受け取った値をどのように使うか（変数に代入したり、式の中で使ったり、print()で表示したり・・・）は、呼び出し側の仕事になる。

つまり、関数をデザインするということは、このような「下請け会社」を設けることに相当し、関数の呼び出しとは、 必要なデータを渡した上で、下請け会社に仕事を発注し、結果を受け取る一連の作業と言えるだろう。 ある意味で、こうした「関数」は、ソフトウェアの部品とも言えるだろう。

そして、複雑な仕事をどのような関数を使って（作って）分業させるか、が、プログラミングの重要なポイントとなる。

５．変数の見える範囲（スコープ）

関数の中の変数は、外からは見えない

関数の中で使われる変数は、他の関数やメイン部で使われる変数とは「干渉」しない。例えば、

def func1():
   x=1
   
def func2():
   x=2
   
#メイン部
x=3

では、それぞれのxは全て異なる「箱」と見なされる。関数の外側からその内側の変数にアクセスするには、引数を仲介にする他ない。 基本的に、変数の見える範囲（スコープ）は、関数の中に限られる。

関数の外側で使われている変数は、関数の内部からでも見える

次のように、メイン部で使われる変数は、関数の内部からでも「覗く」ことができて、下のコードを実行すると 123 とプリントされる。

def func():
   print(x)
   
#メイン部
x=123
func()

ところが、メイン部での変数を関数の内部で変更しようとして、

def func():
   x=456
   
#メイン部
x=123
func()
print(x)

と書いても、プリントされるのは 123 となる。これは、関数 func() 内の変数 x が、関数内限定の（ローカルな）変数と見なされるためである。

もし、メイン部の変数を（「覗く」だけでなく）変更したい場合は、関数内で global x と宣言し、それが「外側」の箱（グローバル変数）であることを知らせる必要がある：

def func():
   global x
   x=456
   
#メイン部
x=123
func()
print(x)

上のコードを実行すると、456 がプリントされる。

　練習：パリティを調べる関数

整数を２進数表示した際、現れる1の個数が偶数の場合を偶パリティ(even parity)、奇数の場合を奇パリティ(odd parity)と言う。 例えば 21 を２進数表示すると 10101 となるから、1が3個、すなわち21は奇パリティである。

非負の整数 n を渡すと、その数が偶パリティなら整数値0を、奇パリティなら整数値1を返す関数 check_parity(n) を設計し、 以下のひな形にその定義を書き加えて、動作を確認しなさい。

# coding: utf-8


# check_parity() の関数定義

# メイン部

n = int(input("非負の整数"))
if check_parity(n)==0:
	print("even parity")
else:
	print("odd parity")

　ヒント

　練習：素数を判定する関数

素数を引数に与えると 1, そうでない場合は 0 を返す、素数判定を行う関数 is_prime(n)をデザインし、 以下のひな形プログラムに書き加えて、正しく動作することを確認しなさい。

# coding: utf-8

is_prime(n):
   関数の中身

# メイン部

for n in range(3,1000,1):
    if is_prime(n)==1:
        print(n)

　ヒント

素数の判定アルゴリズムについては、多重ループ処理のページを参照のこと。

亀場で練習：素数の分布図

亀場を100×100のマス目に区切って、右上隅のマスが1、続いて、横に2, 3, 4, ・・・、そして、右下隅が10000を表すとしよう。 そのとき、素数を表すマス目だけに色を付け、下図のように1〜10000の素数の分布を可視化するプログラムを作成しなさい。

　ヒント

素数の判定には、ひとつ前の演習課題で作成した関数（is_prime(n)）が使えるはず。

マス目を埋めるには、その場所に四角形として描いても良いが、（四角い）点を打ったほうが高速に描画できる。 point()関数を使って点線を描くプログラム例を以下に示す：

# coding: utf-8
from turtle3 import Turtle

ttl=Turtle("localhost")

ttl.clr()
ttl.jump(-256, 0)
ttl.east()
ttl.lw(16)  # 点の大きさを16に設定 
ttl.point() #点を打つモードに切り替える
for i in range(0,32,1):
    if i%2==0:    # iが偶数の時に、現在位置に点を打つ
        ttl.pd()
        ttl.pu()
    ttl.fd(16)

$n$が十分に大きな数のとき、$n$以下の素数の数は$n/\log(n)$個程度であることが分かっている（素数定理）。 つまり、素数の密度はゆっくりと減少する。得られたプロットからその様子（気配？）が観察できるだろうか。