Pythonプログラミング（ステップ５・多重ループ）

このステップの目標

• 多重ループ構造の変数の動きを「シミュレーション」し、プログラムの挙動を予測できる。
• 入出力、式の計算、ループと条件分岐を組み合わせ、複雑な流れのプログラムを構成できる。

1. 多重ループ構造を持つプログラムの基本動作

アルゴリズムを記述しようとすると、ある反復処理をさらに反復するような繰り返し構造、言い換えると、多重のループ構造になるケースは多い。 多重ループは、少ない指示（プログラムの記述量）でコンピュータに沢山働いてもらうための定石、とも言える。 そんな例のひとつとして、次のプログラムの動作を考えてみよう：

for i in range(1,4,1):
   for j in range (1,4,1):
      print("i=",i,"j=",j)

「外側」のforループ（ループ変数i）で反復している内容は、ループ変数jについての内側のfor文

for j in range (1,4,1):
  print("i=",i,"j=",j)

である。そうすると、まずiが1の状態で、内側のfor文が実行され、jが1から3までカウントアップされる。 それが終わると、次にiが2になった状態で、再びjが1から3まで・・・・、という処理が繰り返される。

この様子をまとめると、それぞれのループ変数の動きは以下のようになる：

i=1 j=1　　　　外側のループの１回目　内側のループの１回目
i=1 j=2　　　　　　　　　　　　　　　　　　　　　　２回目
i=1 j=3　　　　　　　　　　　　　　　　　　　　　　３回目
i=2 j=1　　　　外側のループの２回目　内側のループの１回目
i=2 j=2　　　　　　　　　　　　　　　　　　　　　　２回目
i=2 j=3　　　　　　　　　　　　　　　　　　　　　　３回目
i=3 j=1　　　　外側のループの３回目　内側のループの１回目
i=3 j=2　　　　　　　　　　　　　　　　　　　　　　２回目
i=3 j=3　　　　　　　　　　　　　　　　　　　　　　３回目

こうした変数の変化を言葉で表すとすると、内側のjが外側のiよりも「はやく」（あるいは「先に」）動いている、 と言えるだろう。 この例に限らず、

多重ループは内側のループ変数が『先に』（はやく）」回る

と言える。

試しに、上のプログラムをほんの少しだけ改変して（内側のループの継続条件に注目）

for i in range (1,4,1):
   for j in range(1,i+1,1):
       print("i=",i," j=",j)

とすると、こんどは出力が

i=1 j=1　　　　外側のループの１回目　内側のループの１回目
i=2 j=1　　　　外側のループの２回目　内側のループの１回目
i=2 j=2　　　　　　　　　　　　　　　　　　　　　　２回目
i=3 j=1　　　　外側のループの３回目　内側のループの１回目
i=3 j=2　　　　　　　　　　　　　　　　　　　　　　２回目
i=3 j=3　　　　　　　　　　　　　　　　　　　　　　３回目

となる。内側のforでは for j in range(1,i+1,1): となっているので、 反復回数は変数 i が示す値になるわけだ。 この例のように、内側のループ変数の動く範囲を、「外側」のループ変数で制御するパターンもしばしば登場する。

000
001
002
...
998
999

ループは何重でも入れ子にする（ネストする）ことができる。 実用的な意味はないけれども、000から999までを一気にカウントアップしながら表示 するプログラムは、以下のように書けるだろう。一番下の桁が、一番内側のループ変数に対応している点に注意：

# coding: utf-8
for d2 in range(0,10,1):
    for d1 in range(0,10,1):
        for d0 in range(0,10,1):
            print(d2,d1,d0,sep="")

† 上のコードで、print()文中のsep=""は、複数の項目をプリントする際に入れられる区切り文字（通常は空白1つ）を「空」にするための指示。

三角形を表示するプログラム

多重ループを使って、画面上に * を並べて三角形を表示するプログラム例を以下に示す。

# coding:utf-8
for i in range(0,30,1):
   for j in range (0,i,1):
       print("*",end="")
   print()

† print()中の end="" は、出力後の改行を禁止するための指示。

プログラムの構造は、iとjをループ変数とする二重ループになっている。 内側のループでは、アスタリスクを i 回プリントしており、おしまいに「改行」を出力している。 外側のループでは、アスタリスクの個数に対応する変数 i が、0, 1, 2, 3,... ,29まで、順次変化する。 その結果、行あたりの * の個数が順に増えて、三角形に見えるわけだ。

　練習：三角形のバリエーション

     *
    **
   ***
  ****
 *****
******
...

以下の点について、頭の中でまず予想し、次いで、実際にプログラムを動かして確認してみなさい：

• 外側のfor文の i < 30 の箇所を i < 10 に書き換えたら、結果はどのように変わるか
• 内側のfor文の j < i の箇所を j < i*2 に書き換えたら、結果はどのように変わるか
• 三角形を逆向き（頂点が下向き）にするには、どこを変更したらよいか
• 左図のように「右寄せ」にするには、どのように変更したらよいか

亀場で練習：正６角形の繰り返し

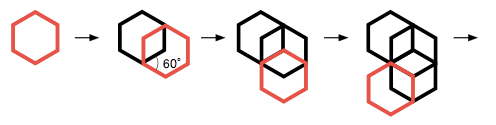
タートルグラフィックスのページのページに紹介されている図形の例のうち、正６角形をずらして重ね合わせてできる図形を二重ループを使って描くプログラムを作成しなさい。

　ヒント

6角形の角度を60°ずつ変えながら、6回描けばよい。

2．二重ループを使った計算

少ない指示で計算機に沢山働いてもらう例として、素数のリストを作成するプログラムをここで作成してみよう。

そのために、まず、ある数nが素数かどうかを、プログラムで判定する方法を考えてみる。 素数とは、自分自身と１以外では割り切れないような自然数だから、最も愚直なやり方は

となるだろう。約数の個数を数え上げるには、もちろん、「総和のパターン」を使えばよい。

素数のリストを作成するには（$n=1,2$ は自明だから、$n=3$ から始め、$n=1000$ の範囲まで調べるとすると）、 次のような手順で計算を行えばよいはずだ。 ここで counter は、総和のパターンに従って約数の数を数え上げるために使う変数名とする。

つまり、プログラムの基本骨格は、nについてのループの中に、mについてのループが入り込んだ 二重ループ構造となるはずだ。 ここで、nが変化する都度、counterを0にセットしなければならない点にも、注意が必要である （さもないと、「以前」のnについてのcounterの値を引きずってしまう）。

　練習：素数探し

上に述べた手順に沿って、3から1000までの範囲で素数を探索し、一覧をプリントするプログラムを作成しなさい。

単にリストが表示されるだけではなく、「ヒント」を読んで、明らかに無駄な計算をしない工夫をプログラムに施すこと。

　ヒント

nがmで割り切れるかどうかを確認する作業をPythonで記述すると、以下のようになるだろう（プログラムの一部分）：

n=調べたい数
for m in range(2,n,1):
    if n%m==0: 
    	print(n,"は",m,"で割り切れた)

ここで、 n%m は「$n$ を$m$ で割った余り」である。つまり、条件文 if n%m==0: は、 「$n$ が $m$ で割り切れたなら（余りが0に等しければ）」という意味になる。

念のため、全体のプログラムのひな形を以下に示す：

# coding: utf-8

for n in range(3,1001,1):
	for m in range(2,n,1):
		????
		????
		????
	?????
	?????

さらなるチューニング

上で述べた方法は、あまりスマートとは言えない。 というのは、全ての $n$ ごとに、2から $n-1$ までの $m$ について割り切れるかどうかを調べているからだ。 もしも $n$ の約数となる $m$ が１つでも見つかったら、その時点で $n$ が素数ではないことは分かってしまう。 なのに、その先の $m$ についても調べ続けるのは、明らかに無駄である。

ある条件（この場合は「割り切れた」）が満たされたことが分かったら、そのことを示す「印」を残して、反復を直ちに止めるうまい方法がある。 変数（フラグ）と break 文を組み合わせるやり方だ。 その基本的なパターンを以下に示す。

	flag=0  # フラグをクリアしておく
	for m in range(から,まで+1,1):
	    if 条件:
	        flag=1   # フラグを立てて 
	        break    # ループを抜ける
	
	if flag==1:      # フラグの値をチェック 
	   print("条件に合致するmが見つかりました") ;
	else:
	   print("条件に合致するmは見つかりませんでした")

「約数のカウントアップ方式」から、「約数が見つかったら打ち切る方式」にプログラムを改造するのは容易なので、ここまでを、この課題の要求水準とする。

その他の効率化のヒントを以下に挙げる：

2以上の偶数は素数ではないことは明らかなので、そもそも調べる必要がない。

$n$ が約数 $m$ を持つ（すなわち $n = k \, m$）とすると、明らかに $m$ は $n$ の平方根よりも大きくなることはない。つまり、ある数 $m$ で割り切れるかどうかの判定の際、$m \le \sqrt{n}$ の範囲だけ調べれば十分。$n,m \gt 0$ だから、この不等式は $m^2 \le n$ と等価。つまり、平方根を実際に計算する必要はない。

さらに効率的に素数をリスティングする方法として、エラトステネスのふるい(Sieve of Eratosthenes)と呼ばれるアルゴリズムが有名だ。 また、大きな数が素数かどうか「当たりをつける」ための良く知られた方法にフェルマーテスト(Fermat primality test）がある。 これらをキーワードに、ウェブ等で調べてみるとよい。大きな素数を探すこと自体が数学的な（意味のある）チャレンジであり、 素数を効率的に見つける方法を巡って、奥の深い探求が続けられている。

　練習：Vièteの式の評価

Viète's formula として知られる $$ \frac{\sqrt{2}}{2} \cdot \frac{\sqrt{2+\sqrt{2}}}{2} \cdot \frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2} \cdots = \frac{2}{\pi} $$ を、実際に上式の左辺を数値計算して確認するコードを作成しなさい。

　ヒント