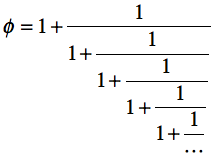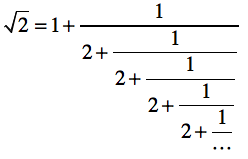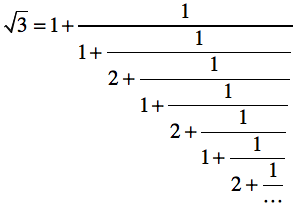Pythonプログラミング(ステップ4・反復処理)
このステップの目標
- 反復処理の流れと、変数の初期値、反復中の変化、終了の判定方法を的確に把握できる。
- for文を使って、ループを含む基本的な処理を記述できる。 特に、「総和」、および「条件が満たされるまで繰り返す」パターンを応用できる。
0.準備
反復処理のプログラムに間違いがあると、期待に反して「いつまで経ってもプログラムが終了しない」ことがある。アプリが「固まった」状態だ。そんな状態から脱し、処理を強制的に中断するには、以下のようにすればよい:
- TurtleEditを使っている場合は、ボタンを押す。
- Google Colabを使っている場合は、コードセルの ■ ボタンを押すか、メニューの「ランタイム」から「実行を中断」を選ぶ。
- Linuxのターミナル(端末エミュレーター)で作業している場合は、プログラム実行中にキーボードの下段にあるコントロール(Ctrl)キーを押したまま、アルファベットのc(コントロールC, CTRL-C)を押す。
1. 反復処理
コンピュータは、長大で人間には面倒な処理でもあっと言う間にこなすことができるから役に立つわけだが、その全てのステップを人間が書き下さなければならないとしたら、プログラムを記述する手間や時間が膨大となりすぎ、本末転倒だ。 コンピュータが役に立つには、少ないプログラムの記述量で、膨大な処理ステップをこなすことができる、そんな仕掛けが不可欠なのだ。
そのために必要となるのが、繰り返し処理、あるいは反復処理だ。その意味で、反復は自動化の要と言える。 反復をマスターしなければ、プログラミングを学ぶ意味が無い。
同じ内容を決まった回数だけ繰り返す
反復の中で最も単純なのは、全く同じ動作の繰り返しであろう。 ただし、繰り返しはどこかで止めないといけない(でないと、永遠に終わらない)ので、繰り返しの回数は決めておく必要がある。 例えば、画面に "Hello!" と10回表示するためのアルゴリズムは以下のように表現できる:
画面に"Hello!"と10回プリントするアルゴリズム
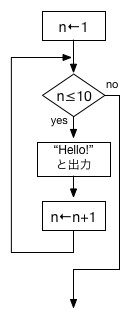
1: 繰り返しの回数をカウントする変数 n を用意する 2: n ← 1 3: もしも n ≤ 10 なら引き続き以下を行い、そうでなければ 7: に移る 4: "Hello!"とプリントする 5: n ← n + 1 (nの値を1つ増やす) 6: 3:に戻って繰り返す 7: 終了する
このアルゴリズムでは、0回目、1回目、2回目、とカウントするための変数 n を用意して、繰り返しの回数をコントロールしている。 一番最初に n を0にしておいてから、 "Hello!"をプリントする都度、n の値を1ずつ増やし、10以上になったら繰り返しを止める。 そうすれば、"Hello!"は全部で10回プリントされることになる。
これをPythonのコードに翻訳すると、以下のようになる:
n=1
while n<=10:
print("Hello!")
n=n+1
ここで while 条件式: は、条件が満足されている間(while the condition is satisfied)、ブロックを反復せよ、という働きをする。
このアルゴリズムを以下のように言い換えても、その意味するところは全く同じである:
1: 1から始めて10まで、1つずつ数が増えるようなリストを作成する([1,2,3,4,5,6,7,8,9,10]) 2: リストからひとつずつ順に数を取り出しながらリストの末尾に至るまで 4: までを行う: 3: "Hello!"とプリントする 4: 繰り返しここまで 5: 終了する
こちらのアルゴリズムをPythonのコードに翻訳すると:
for n in range(1,11,1):
print("Hello!")
注意: range(から, 未満, ずつ)の各項目は整数でなければならない。range(0, 10, 0.1)のような書き方はできない。
ここで range(1,11,1) は、1からスタートして10まで、1ずつ数が増えるようなリストを表しており、
for n in リスト:は、リストの中から順にデータを変数nに取り出しながら、以下のブロックを実行する指示である。
range( )の中で、10ではなくて11が登場するのは、「1ずつ増やして11未満になるまで(つまり10が上限)」を表現するためである。
そのため、range(1,11,1) の中で11のところを101に変えれば, "Hello!" が100回プリントされるし、1001にすれば1000回出力される。
このような、「決まった繰り返し」を表現する際は、range(「から」,「未満」,「ずつ」)とforを組み合わせたこちらの方式のほうが直感的にわかりやすいので、良く使われる。
なお、単に、range(100)と書いた場合は、range(0,100,1)と解釈される。
 練習:繰り返し回数を変えてみる
練習:繰り返し回数を変えてみる
上記のプログラムを修正して、画面に "Temptation" と 108回プリントしてみなさい。
内容を変えながら繰り返す
次に、全く同じことの繰り返しではなくて、「何かを変えながら繰り返す」処理を考えてみよう。
電卓の キーは『現在のメモリー値と入力した数値を加え、その値を新たにメモリーにセットする』という動作をする。
また はメモリーをクリア(0にする)、 は、メモリーの内容を呼び出して画面に表示する、をそれぞれ表す。
その例として、ここでは 1から10まで足し算をここでは取り上げる。 1+2+3+4+5+6+7+8+9+10 を、電卓のメモリー加算(M+)キーを使って計算する様子と対比させながら、それと同等な計算をPythonで書いてみたのが以下である。
# coding: utf-8
# 電卓で計算すると・・・
sum = 0 # MC
sum = sum + 1 # 1 M+
sum = sum + 2 # 2 M+
sum = sum + 3 # 3 M+
sum = sum + 4 # 4 M+
sum = sum + 5 # 5 M+
sum = sum + 6 # 6 M+
sum = sum + 7 # 7 M+
sum = sum + 8 # 8 M+
sum = sum + 9 # 9 M+
sum = sum + 10 # 10 M+
print("1から10までの合計:",sum) # MR
|
変数 sum が電卓の「メモリー」に対応することは一目瞭然である。
そして、ここで繰り返されているのは 『sum = sum + 加える数』 のパターンであるが、加える数 そのものは
1, 2, 3,... と1ずつ規則的に変化していることに気づくだろう。
つまり、パターンは反復されているものの、その内容は、毎回少しずつ(ただし規則性をもって)変わっている。
 練習:電卓で地道に計算
練習:電卓で地道に計算
スマートフォン等にインストールされている電卓アプリを開き、上の手順に従いメモリーキーを使って、1から10までの足し算を試してみなさい。
数の足し上げのアルゴリズム
1から10までの総和の計算を、上記の電卓の操作を振り返りながら、繰り返しの記法を使ってまとめると
1: メモリーを0にする (MC) 2: 加える数(nとする)を 1 から 10 まで 1ずつ増やしながら、以下を繰り返す: 3: メモリーにnを加えた数を、新しくメモリーにセットし直す (n M+) 4: 繰り返しここまで 5: メモリーの値を表示する (MR)
となる。 そして、これをPythonに翻訳したのが,次の例題4aである:
例題4a (ex4a.py)
![]()
# coding: utf-8
sum=0
for n in range(1,11,1):
sum=sum+n
print("1から10までの合計:",sum)
例題4aのアルゴリズム
Input:
Output: 等差数列 $1, 2,\cdots, 10$ の和
1: $sum \leftarrow 0$
2: $n$ を1から、10を越えない範囲まで、1ずつ増やしながら、4:までを繰り返す:
3: $sum \leftarrow sum + n$
4: 反復ここまで
5: "1から10までの合計:" に続けて、$sum$の値を出力し、改行して、終了する
例題4aで
変数 n は、繰り返しの「カウンター」の役割に加え、反復の都度変化する部分、すなわち「加える数」を表すことにも使われている。
ここで、プログラム中の sum=sum+n という書き方を今一度確認しておこう。sum=sum+nは、『現在のsumの値にnを加えた値をsumに代入する』操作を表すので、すなわち『sumをn増やす』操作になる。この動作はよく登場するので、短縮形 sum+=n が用意されている。
同様に、『sumをn減らす』は sum=sum-n となり、それを sum-=nと記述してもよい。
まずは動作を確認するため、このプログラム(ex4a.py)を実行してみよう。
 練習:奇数の和と階乗の計算
練習:奇数の和と階乗の計算
例題4aをひな形にして、
- 1から100までの奇数のみの合計($1+3+5+\cdots+99$)を計算するプログラムを作成せよ。
- 1から10をかけ合わせた結果(10の階乗:$10!=1 \times 2 \times \cdots 10$)計算するプログラムを作成せよ。
 ヒント
ヒント
import math しておくと、関数
math.factorial( )
で階乗が計算できるが、ここでは練習のため、いちいち掛け算を行って計算することにしよう。
奇数だけの合計を求めるには、(i)forループの変数nを1から始めて2ずつ増やすようにするか,(ii) forのところはそのままで,ループの中でnの値をチェックしながら,nが奇数の時だけsumに加える、ふたつのやり方がありそうだ。後者を採用した場合,nが奇数かどうかを判断するには、if文を使って、
と記述すればよい。n%2は『nを2で割った余り』であるから、このif文は『nの値を2で割った余りが0に等しくない場合は・・・を実行せよ』という内容になる。
別のアプローチとして、(iii) $k$ を 0 から始めて、$2 k +1$ が100以下の範囲で、1つずつ増やしながら、$2k+1$ の総和を求める、というやり方も考えられる。
$10!$ が計算できたら、もっと大きな数の階乗も計算させてみよう。
検算用の値: $10!=3628800, \ \ 20!=2432902008176640000, \ \ 30!=265252859812191058636308480000000$.
2. 反復を使いこなす
 反復の「定型文」
反復の「定型文」
反復にはいろいろなバリエーションがあるが、ここではその定型的なパターンのいくつかを押さえておこう。
カウントダウン
実数のループ変数
総和のパターン
無限ループ
| 書き方のパターン | コメント |
for x in range(から,を超えない間,ずつ): 反復内容 |
上の例でもたびたび登場したパターン。 range( )の上限の設定に注意が必要。range(0,10,1)もrange(1,11,1)も繰り返しの回数は10回。 |
for x in range(から,を超える間,負の数): 反復内容 |
「ずつ」の箇所に負の数を入れることによって「カウントダウン」が可能。 |
s=0 for n in range(から,まで+1,ずつ): n番目の値の計算・・・ s = s + n番目の値 |
総和
$$
S = \sum_{n=\cdots}^{\cdots} s_n
$$
を計算する場合は、いつもこのパターン。 総和を入れるための変数(左ではs)の初期化も忘れぬように。 |
while True:
・・・
if 条件:
break
・・・
|
whilte文の繰り返し条件を「常に真(True)」にすると「無限ループ」を表す。 文字通り、いつまで経っても繰り返しつづけるプログラムだ。 プログラムはいつかは終了しないと困るので、反復内容の中にif文を置いて、 そこでループを終了させることができる。break が 実行されると、ただちにループを終了して、次のステップ (while文の次)に処理が移行する。 |
同じ結果を得るためのプログラムの書き方は何通りもある。 例題4aのプログラムを上記の「無限ループ」の定型を使って書き直すと、以下のようになる。
例題4aの「無限ループ」バージョン。
# coding: utf-8
sum = 0
n = 1
while True:
if (n>10):
break
sum = sum + n
n = n + 1
print("1から10までの合計:",sum)
「総和」のパターンのための練習
 練習:ゼータ関数の値の評価
練習:ゼータ関数の値の評価
$\zeta(2)=\pi^2/6$を証明したのは、数学者オイラー(Euler, 1735)とのこと。
リーマンのゼータ関数(Riemann zeta function) $$ \zeta(s) = \sum_{n=1}^{\infty} \frac{1}{n^s} $$ は、数学の問題の各所に関係した大変に興味深い対象である。例えば、$\zeta(2)$の値は、以下のように、円周率と関係の あることがわかっている: $$ \zeta(2) = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots = \frac{\pi^2}{6} $$
$\zeta(2)$を求める問題はバーゼル問題として知られている
Pythonの「総和の計算」のパターンに、ゼータ関数を当てはめることで、ζ(2)の値を数値的に評価してみなさい。
 ヒント
ヒント
注:N項目から無限大項目までの「足し残し分」の見積もりとして
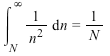
と考えると、N項目で和を打ち切った場合に想定される誤差を(ある程度)予想できるだろう。
import math しておくと、math.piが円周率を与える。
数値計算で無限回の総和を計算することはできない。そこで、どこか大きなnで(例えば1000で)総和計算を打ち切らざるを得ない(左の注も参照)。
Python 2では、総和の各項 1/(n*n)の計算を、整数の範囲で行う(結果は0)。それを避けるには、1.0/(n*n) と記述すればよい。
Python 3では実数の範囲で演算を行なわれる。
# coding: utf-8
import math
s=???
for ?? in range(??,??,??):
??????
zeta2 = math.pi*math.pi / 6.0 ;
print("総和によって求めた zeta(2)=",s)
print("数学的な結果 =",zeta2)
|
 練習:べき乗の計算
練習:べき乗の計算
キーボードから実数($x$とする)と整数($n$とする)を入力すると、(Pythonの累乗計算機能は使わずに)forによる反復で$x^n$を計算し、出力するプログラムを作成しなさい。
まずは、$n\gt0$に対応できれば十分であるが、技量に応じて、$n=0$、$n\lt0$の場合にも対応できるように工夫してみなさい。
 ヒント
ヒント
総和のパターンを応用して、$x$に$x$を$n-1$回掛ければよい($n \gt 0$の場合)。以下にひな形を示す:
# coding: utf-8
x = float(input("x="))
n = int(input("n="))
p=??
for i in range(??,??,??):
????
print(x,"^",n,"=",p)
|
3. 条件が満たされるまで反復する計算
ここでは「人類最大の発明」と言われる複利(compound interest)について考えてみよう
複利で運用される積立があったとしよう。 $x$ 円の元本があったとすると、年利率が$r$ %であったすると、1年目後の積立額は $x \times (1 + r/100)$、 2年目は $x \times (1 + r/100)^2$, そして $n$年目には $x \times (1 + r/100)^n$ となる。
簡単のため、税金や利息端数の切り捨てなどは考えないことにすると、 『年利率(%)を入力して元本が2倍を越えるまでに要する年数を計算するプログラム』は以下のように書ける:
例題4b (ex4b.py)
![]()
# coding: utf-8
r=float(input("年利率(%):"))
n=1
p=1
while True:
p=p*(1+r/100)
if p>2:
break
n=n+1
print(n,"年目に元本は2倍を超えます")
例題4bのアルゴリズム
Input: 年利率(%)
Output: 元本が倍を越えるのに要する年数
1: $r$ に年利率を入力する
2: $n \leftarrow 1$
3: $p \leftarrow 1$
4: 7:までを繰り返す:
5: $p \leftarrow p \times (1+r/100)$
6: もしも $p>2$ならば繰り返しを止め、9:に移る
7: $n$を1増やす
8: 反復ここまで
9: $n$の値を出力し終了する。
例題4bの見どころ
利率計算のアルゴリズムについては、特に説明の必要は無いだろう。
無限ループのパターンwhile True:を使って、元本が何倍になっているのかを表す変数 $p$ が2を越えた時点でループを抜け、繰り返しの回数 $n$ を出力して終了する。
クレジットカードの「リボ払い」は、年利15%(月利1.25%)の元利均等返済の場合が多い。利息は「手数料」に含まれている。
 練習:ローンの計算
練習:ローンの計算
元利均等返済の月利1.25%のローンを組んで100万円を借り入れ、利子も含め毎月2万円ずつ返済したい。各月毎の借入残高をプリントし、借入残高が0になったら停止するプログラムを作成しなさい。
 ヒント
ヒント
元利均等返済では、借金の残高は以下のように推移する(単位は万円):
- 1ヶ月後には、その期間分の利子も含め、借金は $100 \times (1 + 0.0125)$に増えるが、そこから2万円を返済するので、借金の残高は $100 \times (1 + 0.0125) -2 $ になる。
- 2ヶ月後の借金は、1ヶ月分の利子を含め $$\left\{ 100 \times (1 + 0.0125) -2 \right\} \times (1 + 0.0125)$$ になるが、そこから2万円を返済するので、借金の残高は $$\left\{ 100 \times (1 + 0.0125) -2 \right\} \times (1 + 0.0125) -2$$になる。
- 3ヶ月後の借金の残高は、同様に、 $$\left[\left\{ 100 \times (1 + 0.0125) -2 \right\} \times (1 + 0.0125) -2\right]\times(1 + 0.0125) -2$$ になる。
つまり、$n$ヶ月後の借金の残高を$d_n$とすれば、$d_{n+1} = d_n \times (1 + 0.0125) - 2$ の関係が成り立つ。
ひな形
# coding: utf-8
d = 100.0
n = 0
while True:
???
???
???
print(n,"月後の借入残高,d,"万円")
|
 反復を応用した連分数の計算
反復を応用した連分数の計算
以下は、黄金比(golden ratio)と呼ばれる「有理数から最も遠い無理数」( $\phi = (1+\sqrt{5})/2 = 1.618033988\cdots$)を連分数表示したものである。
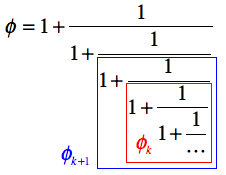
この連分数を、定義に従って「そのまま」数値計算してみよう。 計算にあたっては、「下」から攻めてみるのが良さそうだ。$k$ステップ目の計算値を$\phi_k$とすると、次のステップの値は $$ \phi_{k+1} \leftarrow 1 + \frac{1}{\phi_k} $$ となるはず(下図参照)。
そうすると、この計算を繰り返すことで値が評価できそうだ。 このように、「現在の値」を使って「次の値」を計算する、という手順の繰り返しは、反復処理の典型的なパターンだ。
ここで、$\phi_k$を変数 a、$\phi_{k+1}$を変数 b に対応づけて、もう少し具体的にアルゴリズムをまとめたのが以下である:
初期値(式の$\cdots$のところの値)が分からないのに果たして計算がうまくできるのか心配になるけれども、 「適当な」値から出発しても、最終的には正しい値に収束する。
Input: 計算の打ち切り精度 eps Output: 連分数の近似値 1: aに初期値を設定する 2: 以下を反復 3: b←1+1/a 4: もし |a-b|<eps ならばループを抜けて7:へ 5: a←b 6: 反復ここまで 7: aの値をプリントして停止 |
さらにこれを「無限ループ」の定型に当てはめて、Pythonのプログラムに翻訳すると以下のように書ける。 プログラム中で、ループを何回繰り返すかは陽には指定されておらず、「前」の値と「後」の値の差が十分小さく なったところで繰り返しを抜けるように書かれている。
例題4c (ex4c.py)
連分数を使って黄金比を計算するプログラム例
abs( )は絶対値を返すPythonの関数
# coding: utf-8
import math
a=1.0
while True:
b = 1+1/a
if abs(a-b)<0.0001:
break
a = b
print("計算結果=",a)
print("数学的な結果=",(1.0+math.sqrt(5.0))/2.0)
「条件が満たされるまではずっと反復」の定型のための練習課題
 練習:連分数の計算
練習:連分数の計算
黄金比のプログラム例を参考に、$\sqrt{2}$または$\sqrt{3}$の値を以下の連分数を使って評価するプログラムを作成しなさい。
 ヒント
ヒント
繰り返しの「単位」を上手に見極めること。いずれも「最後の1回分」だけ、式のパターンが異なる点に注意。
 練習:最大公約数
練習:最大公約数
参考書 例題2.12の最大公約数を求めるプログラムをPythonで記述しなさい。 アルゴリズムとして、参考書で説明されているユークリッドの互除法(Algorithm 2)を用いること。
Algorithm 2 Euclidの互除法
Input: 整数 a,b Output: a,bの最大公約数 gcd(a,b) 1: b≠0の間は2:-4:を繰り返す 2: aをbで割った余りをrとする 3: aに現在のbの値を代入する 4: bに現在のrの値を代入する 5: 反復ここまで 6: b=0になったら、この時点でのaの値を出力して停止する |
 練習:自然数の「ひっくり返し」
練習:自然数の「ひっくり返し」
参考書 例題2.11のプログラム(Algorithm 1)をPythonによって記述し、動作を確認しなさい。
- 自然数$n$をひとつ入力する。
- $n$を10進で逆から読んだ自然数を出力する。例えば$n=7463$なら、出力は$3647$になる。
Algorithm 1 数のひっくりかえし
Input: 自然数 n Output: nを逆から読んだ自然数 1: 変数 ans を用意し、0にセットしておく 2: 以下を反復する: 3: nの1の位の数字を求めて、それを変数oneにセットする 4: ansの末尾に 3:で求めたoneを追記する 5: nの1の位を削除する 6: この時点でnが0でなければ2:に戻る。そうでなければ反復を終了する。 7: この時点でのansの値を出力して停止する |
 ヒント
ヒント
10進で表されている自然数 $n$ の1の位は、剰余演算を使って、n%10 で得られる。$n$の桁を1つ右にシフトする(ずらす)には n = n//10 ;、左にシフトするには n = n * 10すればよい。
例えば、n=1234;とすると、n//10は123なので、 nの桁をひとつ右にずらし、1桁目を削除したことになる。
また、n*10は12340なので、桁をひとつ左にずらし、1桁目に0を追記したことに相当する。
ついでながら、2進数での桁のシフト操作はしばしば必要になるので、Python言語には専用の演算子が用意されている。$n$を$k$ビット右シフトした値はn>>k、$k$ビット分左シフトはn<<k と記述できる。nが正の整数ならば、n << 1は、n*2と同じ結果を与える。
 亀場で練習:正多角形の描画
亀場で練習:正多角形の描画
タートルグラフィックスのページの前半部分をよく読み、反復処理を用いて、半径100の円に内接する大きさの正7角形を描画するプログラムを作成しなさい(ただし、円は描かなくてよい)。