Pythonプログラミング(ステップ7・ランダムウォーク)
このページでは、ランダムウォーク(酔歩)の統計的性質について考える。
1. 一次元の酔歩
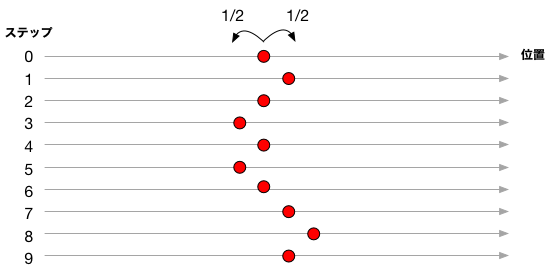
原点から出発した「酔っぱらい」が、それぞれ1/2の確率で、歩幅1で前進または後退を繰り返している様を考える。 前進と後退を等しい確率で繰り返すのであるから、平均としては同じ場所にとどまるはずだが、 それでもフラフラと、かなり遠くまでたどり着くような瞬間もあるだろう。
酔っぱらいの位置を赤丸で示した。 左右に1/2の確率でフラフラと移動する様子。
1回のステップで +1進む確率が1/2、-1進む確率が1/2であるから、 1回あたりの変位を確率変数 $X$ で表すと、その確率密度はデルタ関数を使って $$ p(x) = \frac{1}{2} \left( \delta(x+1) + \delta(x-1) \right) $$ と表すことができる。 その平均は $$ E(X) = \int \, x \, p(x) \, dx = -1/2 + 1/2 = 0 $$ 分散は $$ V(X) = \int \, x^2 \, p(x) \; dx - \left(\int \, x \, p(x) \, dx\right)^2 = 1/2 + 1/2 = 1 $$ である。
$n$歩進んだ後の位置は $$ Y = X_1 + X_2 + \cdots + X_n $$ であるから、その平均は $$ E[Y] = \sum_{i=1}^n E(X_i) = 0 $$ である。
他方で、$X_i$と$X_j$ ($i \neq j$ )が無相関、すなわち $$ E[X_i X_j] = 0 \;\; \textrm{for} \; i \neq j $$ であるから、$Y$の分散は $$ V[Y] = E[(X_1 + X_2 + \cdots + X_n)^2] = \sum_{i,j} E[X_i X_j] = \sum_{i=1}^n E[{X_i}^2] = n $$ である。
つまり、平均の位置は0で、分散(平均二乗変位)が$n$(標準偏差が$\sqrt{n}$)であって、これは、我々の当初の「予想」を裏付けるものである。
酔っぱらいの位置を縦軸に、ステップ数を横軸に取って、長い時間の振る舞いを図示するPythonコードとその出力例を以下に示す。 行きつ戻りつ、その振れ幅がステップ数(時間)と共に増大する様子がわかる。 上での議論から、その「振れ幅」は、ステップ数$n$に対して、$\sim \sqrt{n}$ で増える。
# coding: utf-8
import matplotlib.pyplot as plt
import random
steps = [ ]
xvals = [ ]
maxstep=1000
n=0
x=0
while n<maxstep:
x += random.choice([-1,1])
steps.append(n)
xvals.append(x)
n += 1
plt.title("ONE-DIMENSIONAL RANDOM WALK")
plt.plot(steps,xvals, color=(1.0,0,0.0), linewidth=1.0)
plt.xlim(0,maxstep)
plt.xlabel('TIME')
plt.ylabel('X')
plt.grid(True)
plt.show()
+1と-1の移動を等しい確率で繰り返すだけにもかかわらず、大きな偏差が現れ、そのときはまるで「上昇」や「下降」のトレンドがあるように見える。 これは、一種の公平なギャンブルにおける所持金の変動のモデルとみなすことができる。
2.分布関数
では、$n$ステップ後の移動量$Y$はどのような分布に従うのだろうか。 +1ステップが$k$回、-1ステップが$n-k$回選ばれたときの移動量を$y$とすると $$ y = + k - (n-k) = 2k - n $$ である。 そのようなパターンが選ばれる確率は、 $n$の中から+1を$k$個選ぶ場合の数にそれぞれの生起確率を乗じて、 $$ p(k) = { n \choose{k}} \left(\frac{1}{2}\right)^n = \frac{n!}{k! (n-k)!} \frac{1}{2^n} $$ となる。その対数を取ると $$ \log p(k) = \log n! - \log k! - \log (n-k)! - n \log 2 $$ ここで、スターリングの公式(近似式) $$ \log x ! \approx x \log x - x + \frac{1}{2} \log(2\pi x) $$ を代入すると、 $$ \begin{eqnarray} \log p(k) & \approx & n \log n - n + \frac{\log(2\pi n)}{2} - k \log k + k - \frac{\log(2\pi k)}{2} \\ & - & (n-k) \log (n-k) + n-k - \frac{\log(2\pi (n-k))}{2} - n \log 2 \\ & = & n \log n + \frac{\log n}{2} - k \log k - \frac{\log k}{2} - (n-k) \log (n-k) - \frac{\log(n-k)}{2} - n \log 2 -\frac{\log(2\pi)}{2} \\ \end{eqnarray} $$
ここで、$y = 2k - n$、すなわち $$ k = \frac{n+y}{2} $$ と置きかえる。
これを$\log p(k)$の式に代入し、対数関数のところを $$ \log\left(\frac{1}{2}(n \pm y)\right) = \log\left( \frac{n}{2} \left(1 \pm \frac{y}{n} \right)\right) = \log\left(\frac{n}{2} \right) + \log\left(1 \pm \frac{y}{n} \right) $$ のように変形する。ここで $y \ll n$ を仮定すると、対数関数を展開できて $$ \log \left(1 \pm \frac{y}{n} \right) = \pm \frac{y}{n} - \frac{1}{2} \left(\frac{y}{n}\right)^2 + \cdots $$ となる。
$O(1/n^2)$以上の次数の項は無視。
以上を使って、式を整理すると、 $$ \log p(y(k)) \approx - \frac{1}{2} \log n - \frac{y^2}{2 n} - \frac{1}{2} \log(2\pi) + \log 2 $$ が得られる。 ここで、 $$ dk = \frac{1}{2} dy $$ に注意すると、$y$の確率密度が $$ p(y) = \frac{1}{\sqrt{2\pi n}} e^{-\frac{y^2}{2n}} $$ と得られる。すなわち、移動量$y$は、平均0、分散$n$のガウス分布に従うことがわかった。
移動量が$\pm 1$の場合に限らず、1回あたりの平均移動量を0、分散を$\sigma^2$とすれば、中心極限定理によって、 $n$ステップ後の移動量の分布は $$ p(y) = \frac{1}{\sqrt{2\pi n \sigma^2}} e^{-\frac{y^2}{2n\sigma^2}} $$ となる。
特性関数を使った分布関数の導出
$X$の特性関数(分布関数のフーリエ変換)は、デルタ関数の性質を使うと簡単に求めることができて、 $$ \tilde{p}(q) = \int_{-\infty}^{+\infty} p(x) e^{-iqx} dx = \frac{1}{2} \left( e^{iq} + e^{-iq} \right) = \cos(q) $$ となる。 これを使うと、$Y = X_1 + \cdots + X_n$の特性関数 $\tilde{p}_n(q)$ は、 $$ \tilde{p}_n(q) = \cos^n(q) $$ となる。
ここで、 $$ \cos^n(q) = e^{n \log \cos(q)} = e^{n \log\left(1 - \frac{q^2}{2} + O(q^4)\right)} $$ と書き直し、$|q| \ll 1$ を仮定し、対数関数を展開して$q$の2次の項までを取ると $$ \tilde{p}_n(q) \approx e^{-\frac{n q^2}{2}} $$ を得る。
これをフーリエ逆変換すると、分布関数 $$ p(y) = \frac{1}{2\pi} \int_{-\infty}^{\infty} e^{iqy} e^{-\frac{n q^2}{2}} dq = \frac{1}{\sqrt{2\pi n}} e^{-\frac{y^2}{2n}} $$ が得られる。
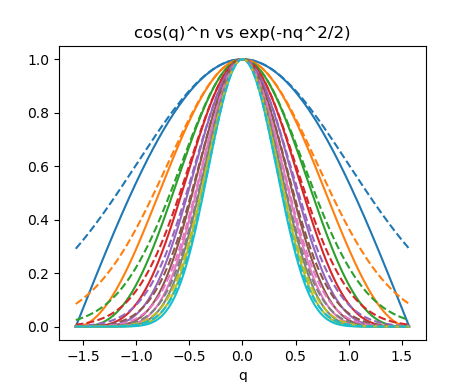
上の議論で、唯一、近似を行っているのは、$\cos^n(q) \sim \exp(-nq^2/2)$ の箇所であった。 $\cos^n(q)$が$n$を大きくするに従ってガウス分布に漸近するのかどうか、その様子を確認するためのPythonコードの例を以下に示す。 $\cos(q)$は$q=0$の近傍で二次関数的に1から減衰するが、それを累乗することによって、$q=0$のごく近傍以外は急激に(指数関数的に)0に漸近し、 全体としては、ガウス分布に漸近している様子がわかる。
# coding: utf-8
import numpy as np
import matplotlib.pyplot as plt
def cosn(q,n):
return np.power(np.cos(q),n)
def gauss(q,n):
return np.exp(-n*q**2/2)
q = np.arange(-np.pi/2, np.pi/2, 0.01)
for n in range(1,11,1):
plt.plot(q, cosn(q,n), '-')
for n in range(1,11,1):
plt.plot(q, gauss(q,n), '--')
plt.show()
上記のPythonコードの出力。
$n=1,\cdots,10$について、実線が$\cos^n(q)$、破線が$\exp(-nq^2/2)$を、それぞれ表す。
頂点の値が1で、上に凸の丸まった分布形を何度も乗じると、1からの距離に応じて指数関数的に裾野がやせ細っていき、
頂点付近の丸みの二次の項の効果のみが強調される。その極限がガウス分布となる。
3. 再帰時間の分布
位置$x$から出発したランダムォーカーが原点(位置0)に$n$ステップで到達する確率を $$ P(n;x) $$ と表記することにする。 そして、その母関数を $$ G(z;x) = \sum_{n=1}^{\infty} P(n;x) z^n $$ と定義する。係数である到達確率のステップ数が$z$のべき指数と対応していることに注意すると($z^1$が「一歩」に対応)、この母関数は、以下のような性質を持つことがわかる:
原点から対称の位置から出発した場合、原点に到達する確率は変わらないから $$ G(z ; x) = G(z ; -x) $$
原点(位置0)から再び原点に戻るには、一旦、その両どなりを経なければならないから、上記の対称性を考慮すると $$ G(z ; 0) = \frac{1}{2} z G(z;1) + \frac{1}{2} z G(z ; -1) = z G(z ; 1) \tag{1} $$ が成り立つ。
同様に、位置1から出発する場合は、1/2の確率で(1ステップで)原点に移動する場合と、 位置2を経て原点に至る場合を加えて、 $$ G(z ; 1) = \frac{1}{2} z + \frac{1}{2} z G(z; 2) \tag{2} $$ と書ける。
$x \ge 2$に対しては $$ G(z ; x) = \frac{1}{2} z G(z ; x-1) + \frac{1}{2} z G(z ; x+1) \tag{3} $$ が成り立つ($x \le -2$についても同様)
右では2次方程式の一方の解を選んでいるが、他方の解は、母関数の係数が負になって、係数が確率を表すという要件も満たさない。
式(3)は$x$についての線形な差分方程式であり、$x \to \infty$でも定義できるためには、 解の形は、$x \gt 0$で $$ G(z ; x) = A e^{-a x} $$ となるはずである($a \gt 0$)。 式(3)にこれを代入すると $$ 1 = \frac{1}{2} z e^{+a} + \frac{1}{2} z e^{-a} $$ となり、$e^{-a}$についての2次方程式になるから、解として $$ e^{-a} = z^{-1} - \sqrt{z^{-2} - 1} $$ が得られる。
また、これをを式(2)に代入すると $$ A=1 $$ が得られる。
よって、式(1)から、$x=0$の母関数が $$ G(z ; 0) = z G(z ; 1) = z e^{-a} = 1 - \sqrt{1 - z^2} $$ と得られる。母関数の定義より、これを級数展開した際の$n$次の項の係数が、原点へ$n$回のステップで再帰する確率となる。 ここで、状況設定をよく考えると、原点から出発してそこに戻るには、必ず偶数回のステップを踏まねばならないから、 $t = z^2$と置き直して、 $$ 1 - \sqrt{1-t} $$ を$t=0$の周りで展開すれば十分である。 $$ \begin{eqnarray} 1 - (1-t)^{1/2} & = & 1 - 1 + \frac{1}{2} t + \sum_{k=2}^\infty \frac{1 \cdot 3 \cdot 5 \cdots (2k-3) }{k! 2^k} t^k \\ & = & \sum_{k=1}^\infty \frac{(2k-2)!}{2^{2k-1} k! (k-1)!} t^k \end{eqnarray} $$
よって、母関数の係数から、原点を出発した酔っぱらいが$2n$回のステップで原点に再帰する確率 $$ P(2n,0) = \frac{(2n-2)!}{2^{2n-1} n! (n-1)!} $$ が得られた。
スターリングの公式 $$ n ! \approx \sqrt{2\pi n} \left( \frac{n}{e} \right)^n $$ を上式に代入して、$n \gg 1$での再帰確率の$n$依存性を調べると $$ P(2n;0) \sim n^{-3/2} $$ であることが容易に確かめられる。 すると、原点に再帰するのに必要な平均ステップ数は $$ \sum_n^\infty 2n P(2n;0) \sim \sum_n^\infty n^{-1/2} \to \infty $$ となって、発散することがわかる。つまり、一旦遠くに離れていったしまった酔っぱらいは、いつまで経ってもなかなか戻って来ない。
 解説:再帰時間分布の確認
解説:再帰時間分布の確認
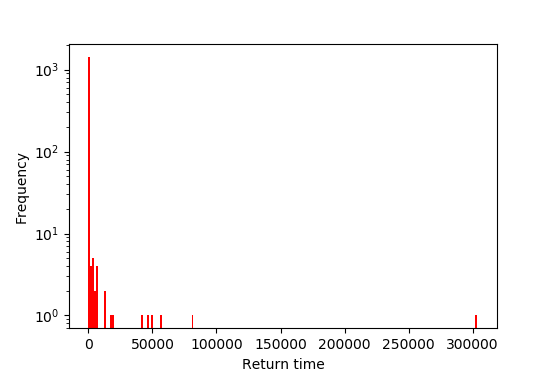
100万ステップの一次元ランダムウォークを行い、原点に再帰するまでに要したステップ数のヒストグラムを描くPythonコードの例を以下に示す。 このように、かなりの回数のステップ数を経ても、上で述べたような漸近的な(べき乗的な)振る舞いを「直視」するのは難しいが、 原点再帰までに非常に長いステップ数を要するケースがときおり発生することは確認できる。
# coding: utf-8
import math
import random
import numpy as np
import matplotlib.pyplot as plt
maxstep=1000000
return_times=[ ]
x=0
n=0
t0=0
while n<maxstep:
x = x + random.choice([-1,1])
n = n + 1
if x==0:
return_times.append(n - t0)
t0 = n
plt.hist(return_times,bins=200,log=True,density=False,cumulative=False,color=(1.0,0,0.0))
plt.xlabel('Return time')
plt.ylabel('Frequency')
plt.show()
上記のシミュレーション結果からは、再帰ステップ数の漸近的な振る舞い $P(2n;0) \sim n^{-3/2}$ までは確認し難い。 そこで、直接分布を調べる代わりに、以下のような手順を考えてみよう:
- 再帰までに要したステップ数を収集する(例:2, 90, 2, 2, 14, 788, 2, 28, ...)
- データを大きいものから順に整列し、ランク付けをする:
ステップ数(降順) 順位 554822214 1 101753846 2 95768144 3 66381232 4 21980350 5 18946996 6 16363204 7 ... 2 22746
- 再帰ステップ数$s$の度数分布を$n(s)$とすると、上記のデータはその累積度数 $$ N(r) = \int_r^{\infty} n(s) ds $$ に他ならない($r$は再帰ステップ数)。
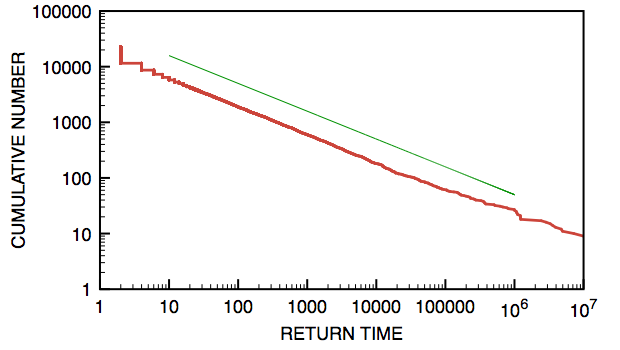
以下は、$10^9$ステップのランダムウォークについて、上記の手順で再帰ステップ数の累積分布を両対数プロットしてみた例である。 グラフからは、$r \gg 1$の領域で $$ N(r) \sim r^{-1/2} $$ がよく成り立っていることが確認できる。 もし、度数分布がべき乗関数 $$ n(r) \sim r^{-\alpha} $$ であれば、累積分布$N(r)$はそれを積分したものだから、 $$ N(r) \sim r^{-\alpha+1} $$ となる。累積分布の指数が$-1/2$であるから、 $$ -\alpha+1 = -1/2 $$ すなわち、分布関数の指数は $$ \alpha = 3/2 $$ となる。
茶色がデータ。比較のため、傾き$-1/2$の直線を緑で描いた。