ガウス(正規)分布
このページでは、ガウス分布の性質や基本的な事項について復習を兼ねてまとめておく。
ガウス(正規)分布
確率や統計の教科書には、必ず、ガウス分布(正規分布) $$ p(x) \, dx = \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^2}{2 \sigma^2}} dx $$ が登場する。 ここで、$\mu$ が平均でベル型の分布の中央の位置、$\sigma$ が標準偏差である。
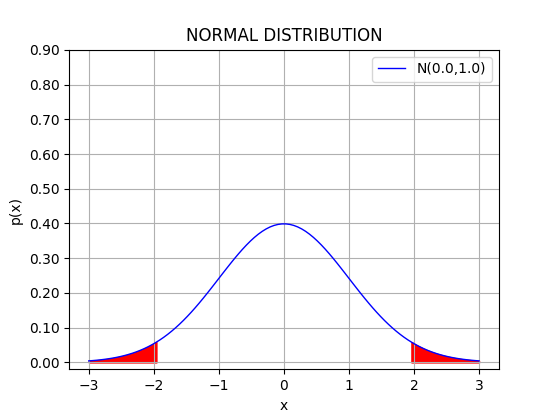
平均0、分散1の正規分布。
赤で示したのは、分布の片側の確率が0.025 (両側で0.05)となる領域で、 凡そ標準偏差の $\pm 1.96$倍以上の範囲に相当。 それ以外のベル型の中央部分が95%の信頼区間に対応。
平均から $\pm \sigma$の範囲には約 68.3%、 $\pm 2 \sigma$の範囲には約 95.5%、 $\pm 3 \sigma$の範囲には約 99.7% の確率が「集中」している。 95%の信頼区間は、$\pm 2 \sigma$の範囲とだいだい等しい。
上の分布をプロットするコード。
# coding: utf-8
import math
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt
mu = float(input('mu='))
sigma = float(input('sigma='))
x = np.linspace(mu-3*sigma, mu+3*sigma, 100)
y = norm.pdf((x-mu)/sigma) / sigma
x0 = np.linspace(mu-3*sigma, mu + norm.ppf(0.025)*sigma, 20)
y0 = norm.pdf((x0-mu)/sigma) / sigma
x1 = np.linspace(mu+sigma*norm.ppf(1-0.025), mu+3*sigma, 20)
y1 = norm.pdf((x1-mu)/sigma) / sigma
fig = plt.figure()
ax = fig.add_subplot(111)
ax.grid()
ax.plot(x, y,'-', color='blue', linewidth=1.0, label="N("+str(mu) + "," + str(sigma**2) + ")")
ax.fill_between(x0,y0,'-', color='red')
ax.fill_between(x1,y1,'-', color='red')
ax.set_title("NORMAL DISTRIBUTION")
yticks = np.arange(0.0, 1.0, 0.1)
yticklabels = ["%.2f" % x for x in yticks]
ax.set_yticks(yticks)
ax.set_yticklabels(yticklabels)
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('p(x)')
plt.show()
以下では、なぜ、ガウス分布があちらこちらに登場するのか、その「仕掛け」について考察してみたい。
最も「単純」な確率密度としてのガウス分布
任意の連続値を取り得る確率変数が従う分布のうちで、いちばん「簡単」な形について考えてみよう。 いかなる分布型であっても確率密度は必ず0以上の値を取るから、一般性を失うことなく、 確率密度関数 $p(x)$ を $$ p(x) = A^{-1} e^{f(x)} $$ と書くことができる。$A$ は規格化定数 $$ A = \int_{-\infty}^{\infty} e^{f(x)} dx $$ である。
ここで、(多くの場合に)自然な仮定として、$p(x)$が$x$の全域で解析的で、かつ、$A \lt \infty$ であることを要請してみる。
仮定から、指数の肩の$f(x)$はある値($\mu$ とする)の周りで展開することができて、 $$ f(x) = c_0 + c_1 (x-\mu) + c_2 (x-\mu)^2 + c_3 (x-\mu)^3 + \cdots + c_m (x-\mu)^m + \cdots $$ となる。 ここで、奇数次の項、例えば $c_1 (x-\mu)$ を考えると $$ e^{c_1 (x-\mu)} $$ は、$c_1 \gt 0$ならば、$x \to \infty$で発散するし、逆に $c_1 \lt 0$ならば、$x \to -\infty$ で発散する。 このように、最大次数の項が奇数次であると、$A$ を有限とすることができない。
また、同様の考察から、偶数次の最大次数の項の係数は負でなければならないこともわかる。 そのような$f(x)$のうちで、最も「簡単」な(展開を最低次で打ち切った)場合、すなわち $$ f(x) = c_0 + c_2 (x-\mu)^2 $$ (ただし、$c_2 \lt 0$。$\mu$を調整することで、一次の項は0とすることができる。)に相当するのが正規分布(ガウス分布)に他ならない: $$ p(x) = A e^{c_0 + c_2 (x-\mu)^2} $$
 参考:コーシー分布
参考:コーシー分布
連続で「簡単」な確率密度の別な構成方法として、$p(x)$が有理関数で表される場合を考えてみよう。 $x$の全域で正値を取り、かつ$\int p(x) dx \lt \infty$となるためには、分子と分母が同じ符号を持ち、分母の次数が分子より2以上大きい必要がある。 そのようなものの中で、項の数が最も少ないのがコーシー分布 $$ p(x) = \frac{1}{\pi (1+x^2)} $$ である。
これを $$ p(x) = \frac{1}{\pi} e^{-\log(1+x^2)} = \frac{1}{\pi} e^{f(x)} $$ と書き直して、指数の肩のところを展開してみると $$ f(x) = -\log(1+x^2) = -x^2 + \frac{1}{2} x^4 - \frac{1}{3} x^6 + \cdots $$ と無限級数になる(この場合は、収束半径 $|x| \le 1$)。
このコーシー分布は、「裾野」の減りかたがゆっくりしていることから、期待値 $$ \int x p(x) dx $$ および分散 $$ \int x^2 p(x) dx $$ が、いずれも定義されない(発散する)。 一方、ガウス分布は、任意のモーメントが値を持ち、各種の平均量を計算することができる。
指定された分散の下でエントロピーを最大にする確率分布
平均と分散を固定した上で、平均情報量(エントロピー)を最大にするような連続な確率分布を考えてみよう。 以下では、平均は0、分散は1と仮定するが、ここでの議論はそれらが幾らであっても同様である。
連続な確率密度関数 $p(x)$ が与えられたとき、そのエントロピー(微分エントロピー)を $$ H = - \int p(x) \log p(x) \, dx $$ と定義する。 エントロピーは、その情報源の「ランダムさ」、「予測の困難さ」、「意外さ」の程度を表す、「情報」の基本的な量的表現である。
ここで、$p(x)$ に別の関数 $\delta p(x)$ を加えてわずかにずらした際、エントロピーがどれくらい変化するか($H$の変分)を考える。 $$ \delta H = - \int \left\{ p(x) + \delta p(x) \right\} \log \left( p(x) + \delta p(x) \right) \approx - \int \left\{ 1 + \log p(x) \right\} \delta p(x) dx $$ $\delta H$を$0$とするような($H$を停留させるような)$p(x)$が、エントロピーを極大にするような確率分布となる。
ただし、この場合、$p(x)$が確率密度であること(積分すると1になる)、そして、平均が0、分散が1に指定されていることの条件が課せられている。 そのような場合は、ラグランジェの未定定数、$\lambda_0, \lambda_1, \lambda_2$ を用いて $$ H' = - \int p(x) \log p(x) dx + \lambda_0 \left[ \int p(x) dx - 1 \right] + \lambda_1 \left[ \int x p(x) dx - 0 \right] + \lambda_2 \left[ \int x^2 p(x) dx - 1 \right] $$ を停留させるような$p(x)$を求めればよい。
停留関数が「最大」を与えるかどうかは、二次の変分まで考える必要がある。 実際に計算すると、二次の変分は負($-1/p(x)$)で、$p^*(x)$は極大であることがわかる。
分散について拘束が無く、かつ、$x$の定義域が有限の場合は、その範囲で一様な確率分布が最大の$H$を与える。 また、$N$通りの離散的な事象の場合は、各事象が等しい確率で生起する場合($p_i=1/N$)に$H$は最大となる。
実際に計算してみると $$ \delta H' = \int \left\{ - 1 - \log p(x) + \lambda_0 + \lambda_1 x + \lambda_2 x^2 \right\} \delta p(x) \, dx $$ となるから、これが$\delta p(x)$に依らずに0となるための条件として $$ - 1 - \log p^*(x) + \lambda_0 + \lambda_1 x + \lambda_2 x^2 = 0 $$ が得られる。すなわち、エントロピーを条件付きで極大にする分布 $p^*(x)$ はガウス分布 $$ p^*(x) = \exp\left( - 1 + \lambda_0 + \lambda_1 x + \lambda_2 x^2 \right) $$ であることが分かった。
 練習:未定定数の決定
練習:未定定数の決定
上の式で、未定定数 $\lambda_0, \lambda_1, \lambda_2$ は、確率密度の規格化 $$ \int \exp\left( - 1 + \lambda_0 + \lambda_1 x + \lambda_2 x^2 \right) dx = 1 $$ および、平均 $$ \int x \exp\left( - 1 + \lambda_0 + \lambda_1 x + \lambda_2 x^2 \right) dx = 0 $$ 分散 $$ \int x^2 \exp\left( - 1 + \lambda_0 + \lambda_1 x + \lambda_2 x^2 \right) dx = 1 $$ の条件から決まる。実際に、これらの定数を求めてみなさい。
独立事象の同時確率が任意の次元で等方的となるような確率分布
確率変数$X$の確率密度$p(x)$が原点からの距離のみの関数であるとすると、一般に$p(x)=f(x^2)$と書けるはずである。 それと独立な$Y$の確率密度を$p(y)$とするとき、結合事象の確率密度は $$ p(x,y) = p(x) p(y) = f(x^2) f(y^2) $$ となるが、$p(x,y)$が原点からの距離のみに依存する(等方的である)とすると、関数方程式 $$ f(x^2) f(y^2) = f(x^2 + y^2) $$ が得られる。 その解は、$x^2$(あるいは$y^2$)の指数関数 $$ f(x^2) = C \exp\left( a x^2 \right) $$ であり($a, C$は定数)、これは平均が0のガウス分布に他ならない。 この事情は、確率変数の数がさらに増えても全く同様である。 言い換えれば、同じガウス分布に従う独立な確率変数の組は、原点を中心として等方的に分布するし、その逆もまた成り立つ。
 練習:関数方程式の解
練習:関数方程式の解
上記の関数方程式を解いてみなさい。
安定な確率分布としてのガウス分布
平均と分散が同じ$n$個の独立な確率変数 $X_1, X_2, \cdots, X_n$ の和 $$ Y = \sum_{i=1}^n X_i $$ を考える。 ここでは、それぞれの平均は0であると仮定する(平均が0でない場合でも、あらかじめそれぞれの$X_i$から平均を差し引いておけばよい)。
もし、$X_i$と$Y$が「同じ」形の確率密度になれば、加算操作について、その分布型が影響を受けないという意味で『安定である』 ということができるだろう。
試みに、ガウス分布する確率変数の和を$n=2$の場合について考えてみると $$ \begin{eqnarray} p(y) &=& \left( \frac{1}{\sqrt{2\pi} \sigma} \right)^2 \int\int dx_1 dx_2 \delta(y - (x_1 + x_2)) e^{-\frac{{x_1}^2}{2 \sigma^2}} e^{-\frac{{x_2}^2}{2 \sigma^2}} \\ &=& \left( \frac{1}{\sqrt{2\pi} \sigma} \right)^2 \int_{-\infty}^{\infty} dx_1 e^{-\frac{{(y-x_1)}^2}{2 \sigma^2}} e^{-\frac{{x_1}^2}{2 \sigma^2}} \\ &=& \left( \frac{1}{\sqrt{2\pi} \sigma} \right)^2 \int_{-\infty}^{\infty} dx_1 \exp \left [ -\frac{ {(\sqrt{2} x_1 - y/\sqrt{2})^2 + y^2/2} }{2\sigma^2} \right] \\ &=& \frac{1}{\sqrt{2\pi} ( \sqrt{2} \sigma)} e^{ -\frac{y^2}{2 (\sqrt{2} \sigma)^2} } \end{eqnarray} $$ となって、$Y = X_1 + X_2$は、分散が2倍(標準偏差が$\sqrt{2}$倍)のガウス分布に従うことがわかる。 同様に、$X_1 + \cdots + X_n$ は、分散が$n$倍のガウス分布となる。 このように確率密度が同じガウス分布の独立な変数の和がガウス分布に「回帰する」ことが簡単に確かめられるので、ガウス分布は『安定』である。
安定な分布は他にも存在するが、平均と分散が有限であるような安定分布はガウス分布のみであることが知られている。
平均値の誤差関数としてのガウス分布(中心極限定理)
母平均$\mu$、母分散$\sigma^2$の集合から$n$個のデータ$X_i$ ($i=1,2,\cdots,n$)をサンプルし、その平均 $$ \bar{X} = \frac{1}{n} \sum_{i=0}^n X_i $$ を考える。 大数の法則によって、$n \to \infty$ で $\bar{X}$ は $\mu$ に漸近する。 ではサンプリングの度に変動する$\bar{X}$は、どのような確率分布に従うのだろうか。
中心極限定理によれば、$n \to \infty$で、$\bar{X}$は平均$\mu$,分散$\sigma^2/n$のガウス分布に漸近する: $$ \bar{X} \sim N(\mu,\sigma^2/n) $$ つまり、標本の誤差は、サンプル数が十分大きければ、母集団の分布型には依存せず、必ずガウス分布(ガウスの誤差関数)に従う。 $n \to \infty$ とはいっても、経験的には $n$が10程度の小さな値であっても、このガウス分布で結果をよく説明することができるので、 その意味で、ガウス分布はとてもありふれた(一般的な)分布と言える。
中心極限定理の導出の手順
確率密度 $p(x)$に従う確率変数$X$について、$e^{-iqx}$という量(ここでの$i$は虚数単位)の平均 $\tilde{p}(q)$ は $$ \begin{eqnarray} \tilde{p}(q) = & \int e^{-iqx} p(x) dx = \int (1 - iqx + \frac{1}{2} (-iqx)^2 + \cdots) p(x) dx \\ & = 1 - iq \mu - \frac{q^2}{2} (\sigma^2 + \mu^2) + \cdots \end{eqnarray} $$ のように書ける。これを $p(x)$の特性関数と呼ぶ。 $q$の一次の項の係数は平均、$q$の二次の項の係数は分散に関係した量になっている。
以上を踏まえて、$\bar{X}$の特性関数を考えると、指数関数の性質($e^{(a+b)} = e^a e^b$)を使って、 $$ \begin{eqnarray} \tilde{p}(q) = & \int e^{-iq\bar{x}} p(\bar{x}) \, d\bar{x} = \int \cdots \int e^{-iq \sum_{j=1}^n x_j/n} \; p(x_1) \cdots p(x_n) \; dx_1 \cdots dx_n \\ & = \left[ \int e^{-iq x/n} p(x) dx \right]^n \end{eqnarray} $$ となる。 上式のカッコの中は $$ \int e^{iq x/n} p(x) dx = 1 - \frac{iq\mu}{n} - \frac{q^2}{2 n^2} (\sigma^2 + \mu^2) + \cdots $$ であるから、特性関数は $$ \tilde{p}(q) = \left[ 1 - \frac{1}{n} \left( iq\mu + \frac{q^2}{2 n} (\sigma^2 + \mu^2) \right) + \cdots \right]^n \\ $$ と書くことができる。
$n$に対する最低限の依存性を知りたいので、$O(1/n^2)$までの全ての項に配慮しながら計算する必要がある。
$n$が$q$に比べて十分に大きければ、右のような式変形(級数展開)が可能である。
従って、$\tilde{p}(q)$を逆変換する際の積分区間は、$\pm n$程度の大きさのところに「カットオフ」があると考えるべきである。
上式を指数関数を使って $$ = \exp\left[ n \log\left( 1 - \frac{1}{n} \left( iq\mu + \frac{q^2}{2 n} (\sigma^2 + \mu^2) \right) + \cdots \right) \right] $$ と書き直した上で、対数関数の部分を展開($\log(1+x) = x - x^2/2 + \cdots$)すると、$1/n^2$の項の$\mu^2$の箇所はちょうど相殺されて、 $$ \begin{eqnarray} \log\left( 1 - \frac{1}{n} \left( iq\mu + \frac{q^2}{2 n} (\sigma^2 + \mu^2) \right) + \cdots \right) & = & - \frac{1}{n} \left( iq\mu + \frac{q^2}{2 n} (\sigma^2 + \mu^2) \right) - \frac{1}{2} \left[ \frac{1}{n} \left( iq\mu + \frac{q^2}{2 n} (\sigma^2 + \mu^2) \right) \right]^2 + \cdots \\ & = & - \frac{1}{n} \left( iq\mu + \frac{q^2}{2 n} \sigma^2 \right) + O(1/n^3) \end{eqnarray} $$ となる。
これを元に式に代入すると、$n \gg 1$ での $\bar{X}$ の特性関数 $$ \tilde{p}(q) \approx \exp\left( - iq\mu - \frac{q^2}{2 n} \sigma^2 \right) $$ が得られる。
フーリエ変換についてはこのページの次節を参照。
この場合、フーリエ逆変換の計算は特に難しいものではなくて、指数関数の肩を$q$について平方完成し
$$
\int e^{-a (q-b)^2} dq = \sqrt{\frac{\pi}{a}}
$$
を当てはめるだけでよい。
特性関数をフーリエ逆変換すると、$\bar{X}$の確率密度関数 $$ \begin{eqnarray} p(\bar{x}) & = & \frac{1}{2\pi} \int_{-\infty}^{\infty} e^{iq\bar{x}} \exp\left( - iq\mu - \frac{q^2}{2 n} \sigma^2 \right) dq \\ & = & \frac{1}{2\pi} \int_{-\infty}^{\infty} \exp\left( iq(\bar{x} - \mu) - \frac{q^2}{2 n} \sigma^2 \right) dq \\ & = & \frac{1}{\sqrt{2\pi \frac{\sigma^2}{n}} } \exp\left[ - \frac{(\bar{x} - \mu)^2}{2 \frac{\sigma^2}{n}} \right] \end{eqnarray} $$ が得られ、$\bar{X}$は($p(x)$には依らず)平均が$\mu$、分散が$\sigma^2/n$のガウス分布に従うことが示された。
【補足】フーリエ変換とその逆変換
中心極限定理の計算に用いた、フーリエ変換とその逆変換の関係について補足(復習)しておく。
ある(性質の良い)関数 $f(x)$ のフーリエ変換を $$ \tilde{f}(q) = \int_{-\infty}^{+\infty} e^{-iqx} f(x) dx $$ と定義する。$x$で積分するので、フーリエ変換は$q$の関数となる。 ここで$f(x)$が確率密度関数であれば、特性関数は、確率密度のフーリエ変換に他ならない。
フーリエ変換された関数は、以下で定義される逆変換で「復元」することができる: $$ f(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} e^{iqx} \tilde{f}(q) dq \\ $$
上式の右辺に $\tilde{f}(q)$ の具体的な表式を含めると、 $$ \frac{1}{2\pi} \int e^{iqx} \left[ \int e^{-iqx'} f(x') dx' \right] dq \\ $$ となる。
この議論は「ズル」である。 というのは、フーリエ逆変換によってきちんと元の関数が復元できるという証明が別にあって、 そのことを踏まえて、右のようなデルタ関数の定義が行われている(右のように定義すると辻褄が合う)からである。
ここで、天下りではあるが、デルタ関数が $$ \delta(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} e^{iqx} dq $$ と表せることを使うと、 $$ \begin{eqnarray} \frac{1}{2\pi} \int_{-\infty}^{\infty} e^{iqx} \tilde{f}(q) dq = \frac{1}{2\pi} \int \int e^{iq(x-x')} f(x') dq dx' \\ = \int \delta(x-x') f(x') dx' = f(x) \end{eqnarray} $$ となって、確かに $\tilde{f}(q)$ から $f(x)$ を「復元」することができた。
 解説: 高分子のモデル
解説: 高分子のモデル
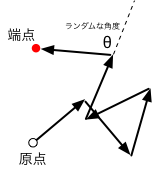
理想化した鎖状の高分子考えてみよう。モノマーを棒に見立てると、棒が任意の角度でつなぎ合わさることで、分子全体として鎖のような構造を形成する。 そのとき、棒同士がぶつかり合う効果は無視することにしよう(棒は互いにすり抜けられると仮定する)。 $i$番目のモノマーの向きと長さをベクトル $\vec{X}_i$ で表し、原点から順に$n$個連なっているとすると、端点の位置ベクトル $\vec{Y}$ は $$ \vec{Y} = \sum_{i=1}^n \vec{X}_i $$ である。 そして、$X_i$が互いに独立でランダムな長さ・向きを取るとき、$n$が十分に大きければ、中心極限定理により($\vec{X}_i$の確率密度の詳細に関わらず)端点はガウス分布する。 これは、高分子科学の分野で理想鎖(ガウス鎖)と呼ばれているモデルに他ならない。
2次元でランダムに回転する長さ1の棒の鎖について、その様子をシミュレーションするPythonコードの例を以下に示す。 このコードでは棒を100個繋げて(薄紫で表示)、一方の端は原点(画面中央)に固定の上、他方の端を赤い点で示すようにしている。
# coding: utf-8
import pyglet
from pyglet.gl import *
import random
import math
import numpy as np
wsize = 512
config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(wsize,wsize,config=config,resizable=False)
win.set_caption('Ideal chain')
win.set_fullscreen(False)
end_points=[ ]
loop_cnt=0
def loop(dt):
global loop_cnt
loop_cnt += 1
if loop_cnt>10000:
pyglet.clock.unschedule(loop)
return
def draw_chain(dt):
glClear(GL_COLOR_BUFFER_BIT)
glClearColor(1,1,1,1)
glLineWidth(2)
glColor3d(0.8,0.8,1.0)
glBegin(GL_LINE_STRIP)
x=0.0
y=0.0
for _ in range(100):
a = random.uniform(0,math.pi*2)
dx = math.cos(a)
dy = math.sin(a)
x += dx
y += dy
glVertex2d(x,y)
glEnd()
end_points.append([x,y])
glPointSize(2)
glColor3d(1.0,0.0,0.0)
glBegin(GL_POINTS)
for ep in end_points:
glVertex2d(ep[0],ep[1])
glEnd()
glFlush()
@win.event
def on_draw():
glEnable(GL_BLEND)
glBlendFunc(GL_SRC_ALPHA,GL_ONE_MINUS_SRC_ALPHA)
glClear(GL_COLOR_BUFFER_BIT)
glViewport(0, 0, wsize, wsize)
glMatrixMode(GL_PROJECTION)
glLoadIdentity()
glOrtho(-20.0, 20.0, -20.0, 20.0, -1.0, 1.0)
glMatrixMode(GL_MODELVIEW)
glLoadIdentity()
draw_chain(0)
pyglet.clock.schedule_interval(loop, 1/10.0)
pyglet.app.run()
上のPythonコードを実行している様子。 中央から延びた「高分子」を薄紫の折れ線で、その端点を赤い点で示した。
多数回の試行を行うと、中心極限定理によって、赤い点の密度は(二次元的な)ガウス分布に漸近する。
 練習:端点の分布関数
練習:端点の分布関数
長さ1のモノマーが平面上でランダムな角度$\theta$で連結するとき、モノマーのベクトルを$\vec{X}_i$とすると、 $n \gg 1$のときに、そのベクトル和 $$ \vec{Y} = \sum_{i=1}^n \vec{X}_i $$ として与えられる端点の座標は、どのような分布になるか(平均と分散を)考えなさい。