Pythonプログラミング（ステップ７・Box–Muller変換）

このページではBox–Muller変換による正規乱数の生成方法について考える（これから）。

1. 二次元のガウス分布

正規分布に従うような乱数の生成アルゴリズムについて考えてみよう。 前提として、[0,1]の区間の一様乱数を発生する仕掛けはすでに提供されているとする（Pythonの場合は、randomモジュールの中のrandom()関数等）。

ここで、ちょっと遠回りして、平均0, 分散1で、互いに独立なガウス分布に従うような確率変数 $X$ と $Y$ を考えよう: $$ \begin{eqnarray} X & \sim & N(0,1)\\ Y & \sim & N(0,1) \end{eqnarray} $$

次に、$(X,Y)$を二次座標上の「点」と考えてみよう。 正規分布の性質と独立性から、その確率分布は $$ p(x,y) = p(x) p(y) = \frac{1}{2\pi} \exp\left( - \frac{x^2+y^2}{2} \right) $$ となる。 これを極座標 $$ \begin{eqnarray} x & = & r \cos(\theta) \\ y & = & r \sin(\theta) \end{eqnarray} $$ で表現してみると、 $$ p(x,y) dx dy = \frac{1}{2\pi} \exp\left( - \frac{r^2}{2} \right) d\theta r dr $$ であり、確率密度は方向角$\theta$には依存しないことがわかる。 すなわち、分布は等方的、言い換えると、$\theta$は$0$から$2\pi$の範囲で一様に分布する: $$ \Theta = 2 \pi U_1 $$ (ここで、(0,1]の範囲の一様乱数を$U_1$とした)。

2. 原点からの距離の分布

つぎに、$(X,Y)$の原点からの距離がどのような確率分布に従うか、考えてみよう。 $Z = X^2 + Y^2$ とおくと、$Z$は自由度2のカイ二乗分布に従うことになる。 このとき、分布関数は指数関数となって、 $$ f(z)=\frac{1}{2} \exp\left(- z / 2\right) $$ である。 一様乱数から指数分布に従う乱数を生成する方法は、こちらに説明した方法を使えばよい。 すなわち、(0,1]の範囲の一様乱数を$U_2$をすると、変数変換によって $$ Z = - 2 \log(U_2) $$ とすれば、$Z$は上記の指数分布に従う乱数となる。 そして、この平方根が、原点からの距離に対応する $$ R = \sqrt{-2 \log(U_2)} $$

3. 標準ガウス乱数の生成

以上をまとめると、正規乱数を発生するアルゴリズムは、以下の通りとなる：

1. (0,1]区間の２つの独立な一様乱数 $U_1$, $U_2$を発生させる
2. $\Theta = 2 \pi U_1$ を計算
3. $R = \sqrt{-2 \log(U_2)}$ を計算
4. $X = R \cos(\Theta)$ を求める
5. $Y = R \sin(\Theta)$ を求める
6. それぞれ独立で平均0、分散1のガウス乱数$X$,$Y$が得られた。

この方法は、Box-Muller変換と呼ばれ、正規乱数を生成する際の標準的なアルゴリズムとしてよく使われている。

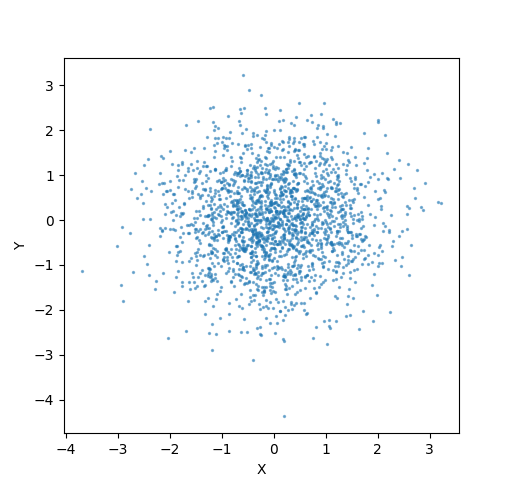
以下は、この方法で１対の乱数を生成し平面上にプロットするコードの例である。

import random
import math
import matplotlib.pyplot as plt

def box_muller():
    u1 = random.random()
    u2 = random.random()
    theta = 2*math.pi*u1
    r = math.sqrt(-2*math.log(u2))
    x = r * math.cos(theta)
    y = r * math.sin(theta)
    return x,y


xlist=[]
ylist=[]
for n in range(2000):
    x,y = box_muller()
    xlist.append(x)
    ylist.append(y)

plt.scatter(xlist,ylist, s=2, alpha=0.5)
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

　練習：マックスウェルボルツマン分布

物理の教科書を見ると、理想気体分子の「速さ」$v$はマックスウェル・ボルツマン分布 $$ f(v)dv = \left[ \frac{m}{2\pi k T} \right]^{3/2} 4 \pi v^2 \exp\left(- \frac{m v^2}{2kT} \right) dv $$ に従うと書かれている($T$は温度、$k$はボルツマン定数,$m$は分子の質量。$0\le v$）。 簡単のため、$m=1$,　$k T=1$とおいて $$ f(v) dv = \sqrt{\frac{2}{\pi}} v^2 \exp\left(- \frac{v^2}{2} \right) dv $$ としたとき、このような確率分布に従う乱数$V$を生成するアルゴリズムを考えて、コードを書いて確認してみなさい。

　ヒント

元々、無相関な気体分子が各方向にガウス分布に従うような速度分布をしているような状況から得られた分布関数であることを思い出す。

「エネルギー」$x = v^2/2$の分布関数として見直して、カイ二乗分布と比較してみるとよい。