Pythonプログラミング(ステップ7・補足・カイ二乗分布)
このページでは、確率や統計の基本的事項であるカイ二乗分布についてまとめておく。
1. 正規分布する確率変数の2乗和
平均0、分散1の正規分布に従うような互いに独立な$k$個の確率変数の組$\{X_1, X_2, \cdots, X_k \}$を考えよう。 そして、これらの二乗和によって「合成」された確率変数 $$ Y = {X_1}^2 + {X_2}^2 + \cdots + {X_k}^2 $$ がどのような振る舞いをするか、考えてみよう。 二乗しているのだから、$Y$が非負の値しか取れないのはもちろんのこととして、 分布も正規分布からは「歪んで」いるはずである。
平均を$\langle \cdot \rangle$で表すことにすると、ひとつの自由度あたり $$ \langle (X_i)^2 \rangle = 1 $$ であり、それぞれは独立なのだから、 $$ \langle Y \rangle = \left\langle \sum_i^k (X_i)^2 \right\rangle = \sum_i^k \langle (X_i)^2 \rangle = k $$ であることはすぐ分かる。すなわち、自由度とともに、分布の「山」は値の大きなほうに移動することになる。
$(X_i)^2$の分散は、$\langle X^2 \rangle = 1$を使って、 $$ \left\langle \left(X^2 - \langle X^2 \rangle\right)^2 \right\rangle = \left\langle X^4 \right\rangle - \langle X^2 \rangle^2 = \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{+\infty} x^4 e^{-x^2/2} dx - 1 = 2 $$ であるから、独立同分布な確率変数の分散の加法性より、自由度$k$のカイ二乗分布の分散は $$ \textrm{Var}(Y) = 2 k $$ となる。
この量は、例えば、ある事象の分散(「ゆらぎ」の二乗平均)を観測し、そのデータを考察する際などに必要となる。
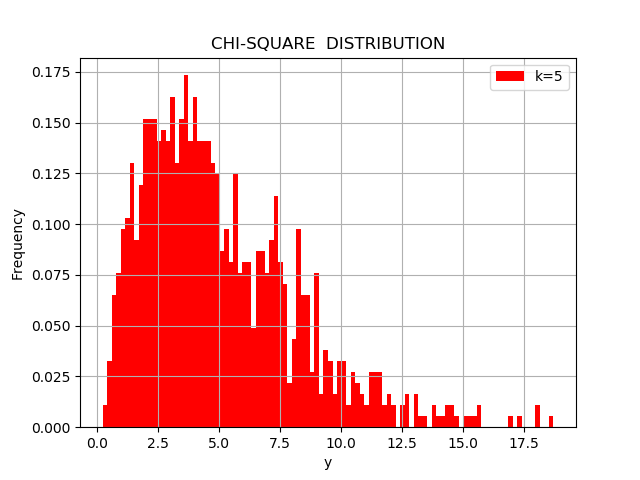
正規分布する乱数の二乗和を1000回発生させ、そのヒストグラムを表示するPythonコードの例を以下に示す:
# coding: utf-8
import math
import random
import matplotlib.pyplot as plt
k = int(input("k="))
ntrial = 1000
ydata=[ ]
for _ in range(ntrial):
y=0
for _ in range(k):
r = random.normalvariate(0,1)
y = y + r*r
ydata.append(y)
plt.title("CHI-SQUARE DISTRIBUTION")
plt.hist(ydata, bins=100, density=True, color=(1.0,0,0.0), label="k="+str(k))
plt.xlabel('y')
plt.ylabel('Frequency')
plt.legend()
plt.grid(True)
plt.show()
$k=5$の場合のシミュレーション結果
2. カイ二乗分布
$Y$の確率密度関数は、その定義通りに書くと、デルタ関数を使って、 $$ f(y;k) = \int_{-\infty}^{\infty} \cdots \int_{-\infty}^{\infty} \delta\left( y - \sum_i^k {x_i}^2 \right) \frac{1}{(2\pi)^{k/2}} \exp\left[-\frac{1}{2} \sum_{i=1}^k {x_i}^2 \right] dx_1 \cdots dx_k $$ となる。 $x_1, x_2, \cdots, x_k$ を極座標に変換し、動径方向の変数を$r$とすれば $r^2 = \sum_{i=1}^k {x_i}^2$ であるから、 $$ \int_0^\infty \delta\left( y - r^2 \right) r^{k-1} \frac{1}{(2\pi)^{k/2}} e^{-r^2/2} dr \int d\Omega $$ となる。ここで、$\int d\Omega$は角度についての積分。
$t = y - r^2$ と変数変換すると、 $$ \begin{eqnarray} f(y;k) & = & - \frac{1}{(2\pi)^{k/2}} \int_{y}^{-\infty} \delta(t) \; (y-t)^{\frac{k-1}{2}} e^{-(y-t)/2} \frac{1}{2(y-t)^{1/2}} dt \int d\Omega \\ & = & \frac{1}{(2\pi)^{k/2}} y^{\frac{k-1}{2}} e^{-y/2} \frac{1}{2 y^{1/2}} \int d\Omega \\ & = & \frac{1}{2 \, (2\pi)^{k/2}} y^{\frac{k}{2}-1} e^{-y/2} \int d\Omega \end{eqnarray} $$
一方、角度についての積分は$k$次元の立体角$\Omega$ (半径1の$k$次元超球の表面積)、すなわち $$ \int d\Omega = \Omega = \frac{2 \pi^{k/2}}{\Gamma\left( k/2 \right)} $$ であるので、以上をまとめると、カイ二乗分布関数 $$ f(y;k) = \frac{1}{2^{k/2} \Gamma(k/2)} y^{\frac{k}{2}-1} e^{-y/2} $$ が得られる。
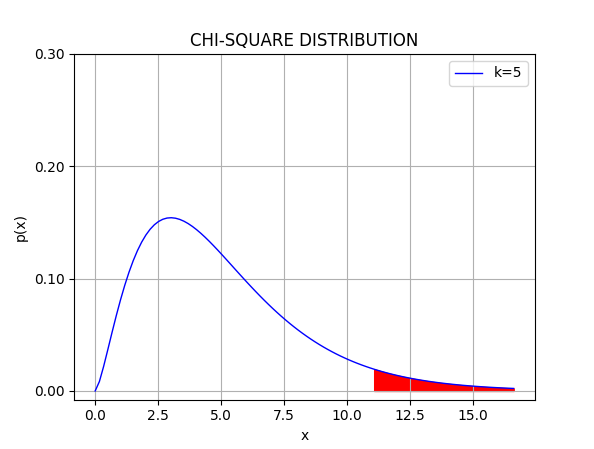
カイ二乗分布をプロットするPythonコードの例。
自由度を入力すると、有意水準5%の棄却域(赤色)と共に、分布が表示される。
# coding: utf-8
import math
import numpy as np
from scipy.stats import chi2
import matplotlib.pyplot as plt
k = int(input('k='))
xc = chi2.ppf(1-0.05,k)
print("Chi-square(0.05)=",xc)
x = np.linspace(0, xc*1.5, 100)
y = chi2.pdf(x,k)
x2 = np.linspace(xc, xc*1.5, 20)
y2 = chi2.pdf(x2,k)
ymax = round(np.max(y),1)
fig = plt.figure()
ax = fig.add_subplot(111)
ax.grid()
ax.plot(x, y,'-', color='blue', linewidth=1.0, label="k="+str(k))
ax.fill_between(x2,y2,'-', color='red')
ax.set_title("CHI-SQUARE DISTRIBUTION")
yticks = np.arange(0.0, ymax+0.1, 0.1)
yticklabels = ["%.2f" % x for x in yticks]
ax.set_yticks(yticks)
ax.set_yticklabels(yticklabels)
ax.legend()
ax.set_xlabel('x')
ax.set_ylabel('p(x)')
plt.show()