Pythonプログラミング(ステップ6・SIRモデル)
このページでは、多変数の微分方程式の例題として、伝染病の流行をシミュレーションしてみよう。
伝染病の流行の微分方程式によるモデル化
以下のような状況で感染が拡大するような疾病(インフルエンザ等)を考える。
- 新型の病気のため、人々は免疫を持っていない。
- 人口が密集しており、人々の行き来が活発で、「平均的に」不特定多数の人と接触している。
- 人口の流入・流出はない(ロックダウンされた国や都市を想定)。
- 接触によって、一定の割合で感染する。
- 感染者は快復後に免疫が生じ、罹患者と再び接触しても再発はしないし、未感染者に罹患させることもない。
そして、未感染(Susceptable)者、感染(Infected)者、および快復した(Recovered)人の3種類が「一様に」混在し、 以下のようなプロセスで感染が伝搬・拡大するような状況を想定する。
モデルの素過程
ここでは、一人ひとりの状態を考えるのではなく、S, I, Rそれぞれの人数の変化として、流行の様子を捉えることにする(ゆらぎの効果は無視する)。 総人口を$N$、未感染者(S)が $x$人、感染者(I)が $y$人、快復した人(R)が $z$ 人と置く。 人口が十分に大きければ、これらを連続量とみなしても構わないだろう。 また、経過時間を変数 $t$(日)で表すことにする。
集団の中で、一人あたり毎日平均 $m$ 人と接触するとする。 そのうち感染している人の割合は $y(t)/N$ であるから、 感染者と非感染者の接触回数は1日あたり $m \frac{y(t)}{N} x(t)$ となる。 それぞれの接触毎に感染が生じる確率を $p$ とすれば、 $\Delta t$ 日の間に生じる新たな感染者は、全体として $$ m \, \frac{y(t)}{N} \, x(t) \, p \, \Delta t $$ となるだろう。 ここで、$\beta = m p / N$ と置くと、$t$日目から $t+\Delta t$日目の間に、新たな感染によって非感染者の数が $$ x(t+\Delta t) - x(t) = - \beta \, x(t) \, y(t) \, \Delta t $$ だけ変化することになる。これを $$ \frac{x(t+ \Delta t) - x(t)}{\Delta t} = - \beta \, x(t) \, y(t) $$ と書き直して、$\Delta t \to 0$の極限を取ると $$ \frac{d x(t)}{d t} = - \beta \, x(t) \, y(t) \tag{1} $$ を得る。
* 新たな感染が無ければ、Iは指数関数的($\sim \exp(-\gamma t)$)に減少し、 IがRになるまでの日数の平均は $1/\gamma$ (日)である。
一方、感染者は1日あたり一定の率$\gamma$で快復してゆくとすると、快復者の増加分は $$ \frac{d z(t)}{d t} = \gamma \, y(t) \tag{2} $$ と書ける($\gamma$は一群の感染者の数が快復によって$1/e$になるまでに要する日数の逆数*)。
人口の流入・流出は考えないので、各人口の総和は一定 $$ x(t) + y(t) + z(t) = N $$ すなわち $$ y(t) = N - x(t) - z(t) $$ であるから、未感染者の人数の変化が $$ \frac{dy(t)}{dt} = - \frac{dx(t)}{dt} - \frac{dz(t)}{dt} = \beta \, x(t) \, y(t) - \gamma \, y(t) \tag{3} $$ となる。
†Kermack and McKendrick(1927)
変形版の例: 2次元正方格子上のSIRモデル
上記はSIRモデル†と呼ばれ、古典的な伝染病の流行モデルのひとつとして知られており、いくつかのバリエーションも含め、その振る舞いが研究されている。
補足
上記のモデルでは、総人口には特段の意味は無いので、変数 $x, y, z$ を総人口に占めるS,I,Rの割合として定義したほうが、色々と見通しが良くなる。 ただし、その場合でも、 $\beta$の内容が$m p$に置き換わるほかは、 モデルの表式は変わらない。
また、上では、(1)から(3)までの3連立の微分方程式としてモデルを書いたが、全人口が保存することから自由度は1つ減るので、 微分方程式として解かなければならないのは (1)と(3)で、$z(t)$は $$ z(t) = N - x(t) - y(t) $$ とすれば十分である。
モデルパラメータから構成される比率(無次元数) $$ R_0 = \frac{\beta N}{\gamma} = \frac{m p}{\gamma} $$ は基本再生産数(basic reproduction number)と呼ばれる。 $R_0$が1より大きい場合に感染者の増大が生じ、1より小さければ感染は終息することが分かっている。
ここで考えているモデルは、人口を分子数(濃度)と置き換えれば、化学反応 $$ \begin{eqnarray} \textrm{S} + \textrm{I} & \to & 2 \textrm{I} \\ \textrm{I} & \to & \textrm{R} \end{eqnarray} $$ と全く同じである。一番目の反応の反応速度が $$ v_1 = \beta [\textrm{S}] [\textrm{I}] $$ 二番目が $$ v_2 = \gamma [\textrm{I}] $$ ということになる。病原体が第一反応、免疫が第二反応を、それぞれ触媒する。
 練習:方程式の無次元化
練習:方程式の無次元化
各変数を $\tilde{x} = x/N, \, \tilde{y} = y/N, \, \tilde{z} = z/N, \, \tilde{t} = m \,p\,t$ のように変数変換(無次元化)することで、 SIRモデルはパラメータをひとつしか含まないかたち $$ \begin{eqnarray} \frac{d \tilde{x}}{d \tilde{t}} & = & - \tilde{x} \, \tilde{y} \\ \frac{d \tilde{y}}{d \tilde{t}} & = & \tilde{x} \, \tilde{y} - \frac{1}{R_0} \tilde{y}\\ \frac{d \tilde{z}}{d \tilde{t}} & = & \frac{1}{R_0} \tilde{y} \end{eqnarray} $$ に変形できることを確かめなさい。
SIRモデルのシミュレーション
二次のルンゲクッタ法を使ってSIRモデルのシミュレーションを行うコードと結果の例を以下に示す。このコードでの状況設定は
- 人口100万人($N=10^6$)で、そのうち10人が初期に感染
- 毎日1人あたり10人に接触。1日・1人の接触あたりの感染率は0.02($m p=0.2$)。
- 感染者の快復日数が14日程度($\gamma = 1/14 \approx 0.07$)。
である(これらの値そのものに強い根拠は無い)。
# coding: utf-8
import math
import matplotlib.pyplot as plt
N = 1000000
x = N-10
y = 10
z = 0
taxis=[ ]
xaxis=[ ]
yaxis=[ ]
zaxis=[ ]
beta=0.2/N
gamma=0.07
dt=0.001
t = 0
cnt=0
while t<180:
if cnt%100==0:
taxis.append(t)
xaxis.append(x)
yaxis.append(y)
zaxis.append(z)
# step 1
kx1 = - beta*x*y
ky1 = beta*x*y - gamma*y
# step 2
t2 = t+dt
x2 = x + kx1*dt
y2 = y + ky1*dt
kx2 = - beta*x2*y2
ky2 = beta*x2*y2 - gamma*y2
# update
x = x + (kx1+kx2)*dt/2
y = y + (ky1+ky2)*dt/2
z = N - x - y
t = t + dt
cnt = cnt + 1
plt.title("SIR MODEL")
plt.plot(taxis,xaxis, color=(0.0,1,0.0), linewidth=1.0, label='S')
plt.plot(taxis,yaxis, color=(1.0,0,0.0), linewidth=1.0, label='I')
plt.plot(taxis,zaxis, color=(0.0,0,1.0), linewidth=1.0, label='R')
plt.xlim(0,180)
plt.legend()
plt.xlabel('DAY')
plt.ylabel('X, Y, Z')
plt.grid(True)
plt.show()
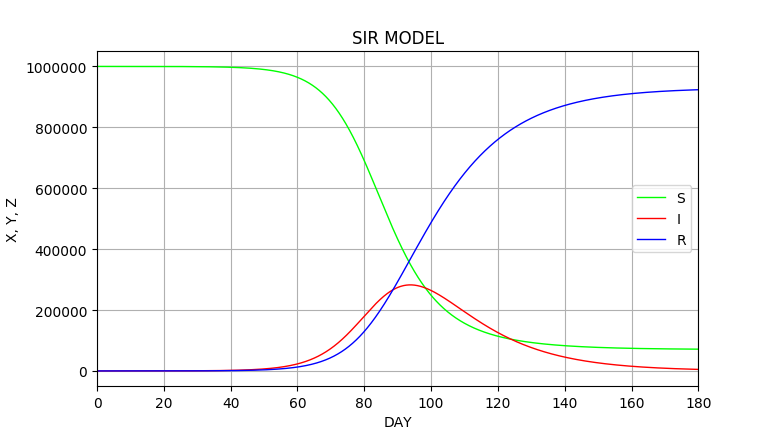
シミュレーション結果の例。
赤が感染者数。この場合、ピーク時には人口のおよそ1/3が発病しており、最終的には9割以上が感染することになる。 また、感染者の立ち上がりは速く、収束は長引く傾向があることが示唆される。
 練習:シミュレーション:爆発的な感染拡大の抑止
練習:シミュレーション:爆発的な感染拡大の抑止
上記のコードで、初期の感染者数, beta, gamma を変えてシミュレーションし、感染の拡大・収束にはどのようなシナリオがあり得るかを予想し、
流行のピークを下げるのに効果的と考えられる対策について考察しなさい。
 ヒント:パラメータの目安と状況設定
ヒント:パラメータの目安と状況設定
2019年の暮れ頃から発生した新型コロナウィルス(SARS-CoV-2)の流行では、中国本土を除いた地域での感染者の増加は、感染拡大の初期と思われる2020年2月中頃の段階で、ほぼ指数関数的で、凡そ8日毎に$e \approx 2.7$倍 のペースであった。これを、上述のSIRモデルの式(3)と見比べると $\frac{m p x}{N} - \gamma \approx \frac{1}{8}$ に対応しており、 この時点では世界人口のほとんどが未感染なので $x \approx N$と置けば、荒い見積もりとして $m p - \gamma \approx 0.12$ [1/日]となる。 その後、2020年2月中頃から3月にかけての日本での感染者数をみると、もう少し増加のペースは遅く、$m p - \gamma \approx 0.083$ [1/日]程度であった。
一方、快復までの日数について、根拠は乏しいが、仮に患者が快復によって2週間後に$1/e$まで減少するとすれば、$\gamma=1/14 \approx 0.07$ 程度と見積もれる。
ルンゲクッタ法のような陽解法(1ステップ前の状態がわかれば、次の状態が決まる)では、計算途中でパラメータを変更しても特に問題は生じない。 外出の禁止などの措置によってある時点からパラメータが急に変化した(例えば$m$が急に小さくなった)場合の効果についても、この種のコードで(ある程度は)予測できるはずである。
一定の割合の人口が免疫を持つことで、集団的な感染が抑制されると言われている(集団免疫)。 これは、初期状態でのRの比率が高い場合に相当する。
 練習:4次のルンゲクッタ法
練習:4次のルンゲクッタ法
上記のコードを4次のルンゲクッタ法に書き直し、計算結果の違いをみてみなさい。
 解説: SciPyの利用
解説: SciPyの利用
微分方程式を解くには数値計算ライブラリを活用するのが簡単で確実である。 以下のコードは、SIRモデルの計算にSciPyのodeint関数を用いた例である。
各変数の微分を計算する関数(この例では sir_model)を定義する。
その関数には、変数の値のリスト、時間、そしてパラメータが順に渡されるので、微分値を計算して、それをリスト(配列)で返すようにする。
odeint関数には、その微分を計算する関数名と、初期値のリスト、結果を得たい時刻のリスト、そしてパラメータ(タプル)を与えると、各変数の時系列が返される。 以下の例では、0.1日毎の結果を得た上で、プロットする段では、10点おきに間引いて表示している。
こちらのコードでは、式(1),(2)および(3)を連立させて解くように書いた。
# coding: utf-8
import math
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def sir_model(v, t, beta, gamma):
x = v[0]
y = v[1]
z = v[2]
dxdt = - beta*x*y
dydt = beta*x*y - gamma*y
dzdt = gamma*y
return [dxdt, dydt, dzdt]
N = 1000000
beta=0.2/N
gamma=0.07
dt=0.1
init_vals=[N-10, 10, 0]
times = np.arange(0.0, 180, dt)
args=(beta, gamma)
results = odeint(sir_model, init_vals, times, args=args)
plt.title("SIR MODEL")
plt.plot(times[::10],results[::10,0], color=(0.0,1,0.0), linewidth=1.0, label='S')
plt.plot(times[::10],results[::10,1], color=(1.0,0,0.0), linewidth=1.0, label='I')
plt.plot(times[::10],results[::10,2], color=(0.0,0,1.0), linewidth=1.0, label='R')
plt.xlim(0,180)
plt.legend()
plt.xlabel('DAY')
plt.ylabel('X, Y, Z')
plt.grid(True)
plt.show()