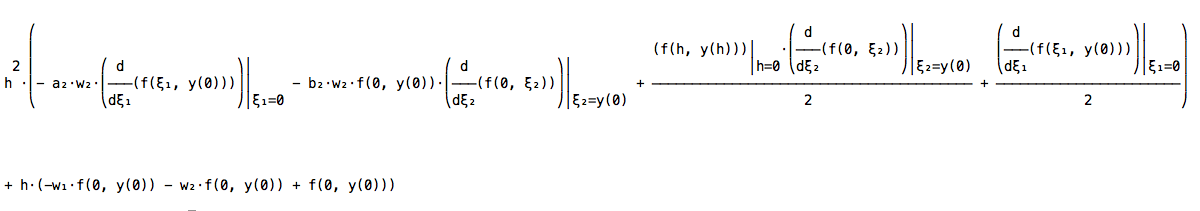Pythonプログラミング（ステップ６・ルンゲクッタ法）

ルンゲクッタ法：実用的な常微分方程式の数値解法

一階の常微分方程式（ordinary differential equation) $$ \frac{d y(x)}{d x} = f(x,y(x)) \tag{1} $$ を考えよう。微分を差分で近似し「総和」の計算パターンに当てはめることで、比較的簡単なコードで数値計算が可能であることを こちらのページですでに紹介した。 ただし、実際にいろいろな問題に適用すると、オイラー法は単純な一方で精度や効率の点で難点もある。 そこで、実用的な手法としてよく使われているのがルンゲクッタ法 (Runge-Kutta method)である。

ルンゲクッタ法は４次の公式が定番であるが、ここではまず２次の公式を導出して、雰囲気を掴んでおこう。

計算のステップを$h$と置いて、$y(x)$とその微分値から、$h$だけ先の未来 $y(x+h)$ を「予測」するための計算式を導きたい。 オイラー法では、それを簡単に $$ y(x+h) = y(x) + f(x,y(x))\,h $$ としていたところを、刻み幅$h$の途中の値も活用して精度がさらに上がるように工夫してみよう。

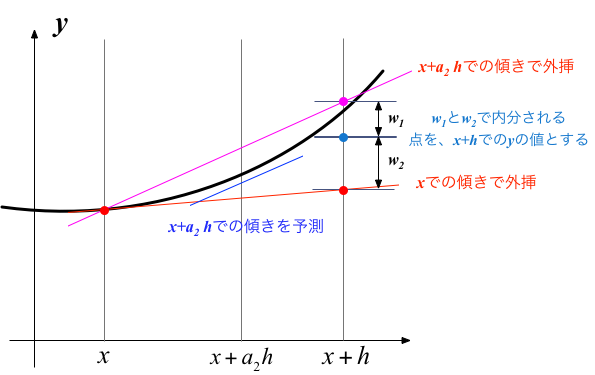
もう少し具体的には、下図のように、$x$と$x+h$の途中点での$y$の変化率（傾き）をまず予測し、その傾きを持つ直線を$x$から外挿し$x+h$での予測値を求める。 「現在」の$x$の傾きを外挿して得た予測値（オイラー法）とこれを組み合わせることで（例えば「平均」することで）、 図のように$y(x)$の変化が一様でない場合でも、予測の精度を上げられるのではないか？

そこでまず$x$での微係数（変化率）を $$ k_1 = f(x,y(x)) $$ とおき、さらにそれを使って、$x+a_2 h$での変化率の「予測」を $$ k_2 = f(x+a_2 h,y(x) + b_2 k_1 h) $$ で見積もることにする。ここで、$0 \lt a_2 \lt 1$ は、$h$をどこで内分するかを決める数、$b_2$は「予測」をちょうどよい加減に整えるための数である （その具体的な値は以下で計算する）。

これらの数を適切に与え、$h$だけ先の値を $$ y(x + h) = y(x) + \left( w_1 k_1 + w_2 k_2 \right) h \tag{1} $$ で見積もるのが、２次のルンゲクッタ法である。

ここで、未知のパラメータ $a_2, b_2, w_1, w_2$ は以下のようにして決める。

$y(x)$の変動を２次のオーダーまで近似

まず、$y$を$x$の周りで２次までテイラー展開する。 $$ y(x+h) = y(x) + y'(x) h + \frac{1}{2} y''(x) h^2 + \cdots $$ ここで、$'$記号は$x$による微分を表す。与えられた微分方程式から $$ y'(x) = f(x,y(x)) $$ さらにそれを微分すると、 $$ y''(x) = \frac{\partial f(x,y)}{\partial x} + \frac{\partial f(x,y)}{\partial y} y'(x) $$ となるから、既知である $f(x,y(x))$ を使って $h$ だけ「先」の値を $$ y(x+h) = y(x) + f(x,y(x)) h + \frac{1}{2} \left[ \frac{\partial f(x,y)}{\partial x} + \frac{\partial f(x,y)}{\partial y} f(x,y(x)) \right] h^2 + \cdots \tag{2} $$ と書くことができた。

時間発展の式を整理する

次に、$k_2$を$(x,y(x))$の周りでテイラー展開すると $$ \begin{eqnarray} f(x+a_2 h,y(x) + b_2 k_1 h) = f(x,y(x)) + \left[ a_2 \frac{\partial f(x,y)}{\partial x} + b_2 k_1 \frac{\partial f(x,y)}{\partial y} \right] h + \cdots \\ = f(x,y(x)) + \left[ a_2 \frac{\partial f(x,y)}{\partial x} + b_2 f(x,y(x)) \frac{\partial f(x,y)}{\partial y} \right] h + \cdots \end{eqnarray} $$ となるから、時間発展の式(1)に$k_1, k_2$の具体的な表式を代入して整理すると、 $$ \begin{eqnarray} y(x + h) = y(x) + w_1 f(x,y(x)) h + w_2 \left\{ f(x,y(x)) + \left[ a_2 \frac{\partial f(x,y)}{\partial x} + b_2 f(x,y(x)) \frac{\partial f(x,y)}{\partial y} \right] h \right\} h + \cdots \\ =y(x) + (w_1 + w_2) f(x,y(x)) h + \left[ w_2 a_2 \frac{\partial f(x,y)}{\partial x} + w_2 b_2 f(x,y(x)) \frac{\partial f(x,y)}{\partial y} \right] h^2 + \cdots \tag{3} \end{eqnarray} $$

パラメータを決める

ここで、時間発展の式(3)が式(2)の２次のオーダーまで完全に一致するようにパラメータを決める （そうすれば、時間発展は$h$の２次までは正しく近似できているはずである）。 式をよく見比べると、そうなるためには、 $$ w_1 + w_2 = 1 $$ かつ $$ w_2 a_2 = 1/2, \;\; w_2 b_2=1/2 $$ であれば良いことがわかる。

二次のルンゲクッタ公式

ここでは、$w_1 = w_2 = 1/2$ を採用することにしよう。すると、$a_2 = b_2 = 1$となる。 その結果、２次のルンゲクッタ公式として

1. $k_1 \leftarrow f(x,y(x))$
2. $k_2 \leftarrow f(x + h,y(x) + k_1 h)$
3. $y(x+h) \leftarrow y(x) + (k_1 + k_2) h/2$

が得られる。

一方、パラメータとして $w_1=0, \; w_2=1, \; a_2 = b_2 = 1/2$ を採用すると、

1. $k_1 \leftarrow f(x,y(x))$
2. $k_2 \leftarrow f(x + h/2,y(x) + k_1 h/2)$
3. $y(x+h) \leftarrow y(x) + k_2 h$

という方法も可能で、こちらは $h/2$の点での値を用いることから「中点法」として知られる。 いずれも$h$について２次の精度の公式になっている。

４次のルンゲクッタ公式

実用的な計算でよく用いられるのは、４次のルンゲクッタ法である。 この場合も考え方は全く同様で、変化率の予想値を４通り求め、それぞれを傾きとする直線で外挿して求められた$x+h$での$y$を加重平均することによって、次のステップの値とする。 具体的に４次の公式を得るには、上記の同様の手続きを$h$について4次のオーダーまで 行えばよいが、それなりに手間のかかる計算となる。

2次の公式の場合もそうであったように、4次の公式でもパラメータの選択には自由度があるが、 良い結果が得られる選択肢として、以下の公式がよく使われている：

　練習：ルンゲクッタ法の実装

ロジスティック方程式 $$ \frac{dy}{dt} = r \left(1 - \frac{y}{N} \right) y $$ を、オイラー法と4次のルンゲクッタ法で「同時に」解くPythonコードを作成しなさい。

0 0.1 0.1
0.1 0.1218701933831344 0.1198
0.2 0.14845172148114733 0.1434729592
0.30000000000000004 0.1807249703527805 0.1717558612395679
0.4 0.21985781692848208 0.2055170319700786
...

のように、$t$と、ルンゲクッタ法とオイラー法で得られた$y(t)$を同時に出力するように工夫しなさい。 パラメータの例として、成長率 $r=2$ 、個体数の上限 $N=10$、初期値$y(0)=0.1$とし、刻み幅 $h$ を変えて、 $0 \le t\lt 10$ の範囲での両者の振る舞い方の違いをシミュレーションしてみなさい。

　解説:数式処理ソフトの利用

単純で手間のかかる計算は数式処理ソフトを使って処理する方法もある。Pythonで使える数式処理用ライブラリとして sympyがある。 以下は、sympyを使って、2次のルンゲクッタ公式を計算するため、式の展開と整理を行うためのPythonコードの例である：

# coding: utf-8
from sympy import *
init_printing()

x,h = symbols("x,h")
f = Function("f")
y = Function("y")

f1 = y(0) + h*f(0,y(0)) + h*h/2*(diff(f(h,y(h)),h).subs(h,0))

a2,b2=symbols("a2,b2")

k1 = f(0,y(0))
k2 = f(0,y(0)) + h * diff( f(a2*h,y(0)+b2*k1*h), h ).subs(h,0)

w1,w2=symbols("w1,w2")
f2 = y(0) + h*w1*k1 + h*w2*k2

# Derivative(y(h), h) --> f(h,y(h))
df = (f1 - f2).subs(Derivative(y(h), h), f(h,y(h)))
r = collect(expand(df), h)

pprint(r)

このコードを実行すると、以下のような出力が得られるので、これが恒等的にゼロになるように係数の関係を決めればよい。

この種の数式処理ソフトとしては他にも、Mathematica（有償）、Maple（有償）、Maxima（無償）等がよく知られている。 これらはsympyよりも歴史があることもあって、使い勝手や機能に優れた点も多い。 以下は、Mapleを使って４次のルンゲクッタのパラメータを求める例である：

f:=x->g(x,y(x));

f1:= y(0) + h*f(0) + h^2/2*D(f)(0) + h^3/6*((D@@2)(f))(0) + h^4/24*((D@@3)(f))(0):

k1 := g(0,y(0)):

k2 := taylor(g(a2*h,y(0)+b2*k1*h),h=0,4):

k3 := taylor(g(a3*h, y(0)+ b3*k2*h),h=0,4):

k4 := taylor(g(a4*h, y(0)+b4*k3*h),h=0,4):

f2 := y(0)+h*w1*k1 + h*w2*k2 + h*w3*k3 + h*w4*k4 :

df0 := convert(f2-f1, polynom):

df1:= subs( ((D@@3)(y))(0)=(D[1, 1](g))(0, y(0))+(D[1, 2](g))(0, y(0))*(D(y))(0)
           +((D[1, 2](g))(0, y(0))+(D[2, 2](g))(0, y(0))*(D(y))(0))*(D(y))(0)
           +(D[2](g))(0, y(0))*((D@@2)(y))(0), df0):
           
df2 := subs(((D@@2)(y))(0)=(D[1](g))(0, y(0))+(D[2](g))(0, y(0))*(D(y))(0),df1):

df3 := subs((D(y))(0)=g(0,y(0)),df2):

res:=collect(expand(df3,h), h) :

simplify(coeffs(res,h)[1]);

simplify(coeffs(res,h)[2]);

simplify(coeffs(res,h)[3]);

simplify(coeffs(res,h)[4]);

上のコードの例では、$x$の原点はどこに置いても一般性は失われないので $x=0$ とし、 $$ k_1 = g(0,y(0)) $$ $$ k_2 = g(0 + a_2 h,y(0) + b_2 k_1 h) $$ $$ k_3 = g(0 + a_3 h,y(0) + b_3 k_2 h) $$ $$ k_4 = g(0 + a_4 h,y(0) + b_4 k_3 h) $$ を用いて、 $$ y(0+h) = y(0) + \left(w_1 k_1 + w_2 k_2 + w_3 k_3 + w_4 k_4 \right) h $$ によって時間発展するスキームを、$y(0+h)$のテイラー展開の4次まで一致するよう、係数の比較を行う。

上記のMapleのコードを実行すると、パラメータが満たすべき条件（連立方程式）が分かるので、それを解くと、上記の公式が得られる：

eq1:=-1/4+w2*b2^3+w3*b3^3+w4*b4^3=0:
eq2:=-1/3+(2*b2*w3+b4*w4)*b3^2+(b2^2*w3+2*b4^2*w4)*b3=0:
eq3:=w3*a3*b3^2+w4*a4*b4^2+w2*a2*b2^2-1/4=0:
eq4:=-24*b2*b3*b4*w4+1=0:
eq5:=-5/24+(b4*(a3+a4)*w4+w3*b2*(a2+a3))*b3=0:
eq6:=w3*b3^2*a2+w4*b4^2*a3-1/8=0:
eq7:=w3*a3^2*b3+w4*a4^2*b4+w2*a2^2*b2-1/4=0:
eq8:=-24*a2*b3*b4*w4+1=0:
eq9:=w3*a2^2*b3+w4*a3^2*b4-1/12=0:
eq10:=w3*a3*b3*a2+w4*a4*b4*a3-1/8=0:
eq11:=w3*a3^3+w4*a4^3+a2^3*w2-1/4=0:
eq12:=-2*a2*w2-2*a3*w3-2*a4*w4+1=0:
eq13:=w3*b3+w4*b4+w2*b2-1/2=0:
eq14:=w3*b3^2+w4*b4^2+b2^2*w2-1/3=0:
eq15:=1+(-6*b2*w3-6*b4*w4)*b3=0:
eq16:=w3*a3*b3+w4*a4*b4+a2*b2*w2-1/3=0:
eq17:=w3*b3*a2+w4*b4*a3-1/6=0:
eq18:=a2^2*w2+a3^2*w3+a4^2*w4-1/3=0:
eq19:=-1+w1+w2+w3+w4=0:
solve({eq1,eq2,eq3,eq4,eq5,eq6,eq7,eq8,eq9,eq10,eq11,eq12,eq13,eq14,eq15,eq16,eq17,eq18,eq19});

【出力結果】
{a2 = 1/2, a3 = 1/2, a4 = 1, b2 = 1/2, b3 = 1/2, b4 = 1, w1 = 1/6, w2 = 1/3, w3 = 1/3, w4 = 1/6}