Pythonプログラミング(ステップ7・SIRモデルのモンテカルロ・シミュレーション)
このページでは、二次元正方格子上の伝染病の伝搬モデル(SIRモデル)のモンテカルロ・シミュレーションを考えてみる。
人の長距離の移動が無い場合の病気の感染
伝染病の古典的なモデルであるSIRモデルでは、人は一様に混じり合って、S, I, Rがそれぞれの密度に比例した確率で接触すると仮定されていた。 これは、交通手段が高度に発展し、遠距離でも隔てなく人々が往来する現代の社会に近い状況かもしれない。
その対局に、人々の往き来が無く、隣人とのみ接触可能な状況も考えられる。 感染拡大の防止のため、遠距離交通が停止し、自宅待機が強いられるようなケースも、どちらかと言えば、こちらの状況に近いだろう。
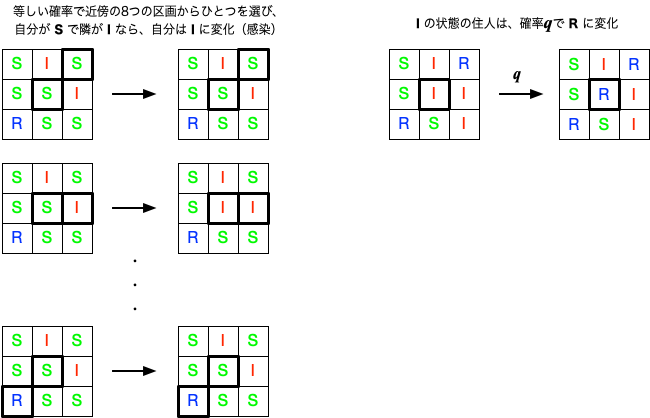
そこで、正方形の区画に仕切られた仮想的な「都市」を考え、それぞれの区画の住人は隣接する8つの区画とのみ接触が可能であったとしよう。 そして、毎日、8つの区画の中からランダムに選ばれた1つと往来する。 もしその住人が未感染(S)であった場合、往来先の区画の住人が感染者であれば、その住人も100%の確率で感染すると仮定しよう。 これは、SIRモデルの説明で、$m \, p = 1$ に相当する。
感染状態(I)の住人は、1日あたり、$q$ の率で快復状態(R)に変化するとしよう。
モデルの素過程
このような状況設定の元で、初期に点在していた少数の感染者(I)から感染がどのように拡大するかをシミュレーションしてみよう。
ここでの説明は疫病の伝搬を想定しているが、例えば、森林の火災の広がり(Sが燃えていない樹木、Iが燃焼中、Rが燃焼後)等のモデルと考えることもできる。
Pythonによるコーディング例
状態Iの場所が1ステップ(日)毎に確率 $q$ でRに遷移するとすると、その場所がIからR に変化するには、平均 $$ \sum_{k=1}^{\infty} k \; (1-q)^{k-1} \, q = 1/q $$ だけ要する。 SIRモデルの説明で用いたパラメータ$\gamma$は、 IがRに変化するまでの平均日数の逆数だったことを思い出すと、パラメータの間には $$ \gamma = q $$ という対応があることがわかる。
基本再生産数の定義 $R_0 = \frac{mp}{\gamma}$ より、$\gamma = \frac{mp}{R_0}$であるから、$R_0$を指定すれば、$\gamma$(そして$q$)も自動的に決まる。
以上を踏まえ、前節のアイデアをそのままPythonコードで表現してみた例を以下に示す。
コードでは、初期の感染濃度を変数p0とし、$100 \times 100$の格子上でシミュレーションを行っている。
変数SCALEは、表示の際の格子の一辺のサイズ(ピクセル数)である。
格子の中からランダムにひとつの場所(サイト)を選び、そのサイトについて、前節で説明したルールを適用する。 それを何度も繰り返すだけの単純なアルゴリズムである。 この種の乱数を用いたシミュレーションは、ギャンブル(カジノ)で有名な地名にちなんで、一般にモンテカルロ・シミュレーション(Monte Carlo simulation)と呼ばれている。
S状態のサイトは水色、I状態は錆色、R状態は灰色で表示される。
このコードは表示のためにpyglet(バージョン1.5.27以前)が必要
# coding: utf-8
import pyglet
from pyglet.gl import *
import random
import math
import numpy as np
# グローバル変数
p0=0.001 # 初期感染密度
N=100 # 1辺の格子数
r0=2.5 # 基本再生産数
SCALE=6 # 格子のサイズ
gamma = 1.0/r0
s=np.zeros([N,N])
counter=0
n_i=0
# 初期化
def init_state():
global s,n_i
for i in range(N):
for j in range(N):
if random.random()<p0:
s[i,j] = 1
n_i += 1
# 状態更新
def update_state(n):
global s,counter,n_i
for _ in range(n):
i = random.randrange(0,N,1)
j = random.randrange(0,N,1)
if s[i,j]==0:
di,dj = random.choice([(-1,-1),(-1,0),(-1,+1),(0,-1),(0,+1),(+1,-1),(+1,0),(+1,+1)])
i2 = (i+di) % N
j2 = (j+dj) % N
if s[i2,j2]==1:
s[i,j]=1
n_i += 1
elif s[i,j]==1:
if random.random()<gamma:
s[i,j]=2
n_i -= 1
counter += 1
def next_frame(dt):
return
def redraw():
update_state(1000)
for i in range(N):
for j in range(N):
if s[i,j]==0:
glColor3d(0.2,0.6,0.7)
elif s[i,j]==1:
glColor3d(0.8,0.3,0.1)
else:
glColor3d(0.2,0.2,0.2)
glBegin(GL_POLYGON)
glVertex2d((i+0)*SCALE,(j+0)*SCALE)
glVertex2d((i+1)*SCALE,(j+0)*SCALE)
glVertex2d((i+1)*SCALE,(j+1)*SCALE)
glVertex2d((i+0)*SCALE,(j+1)*SCALE)
glEnd()
t = counter/(N*N)
r_i = n_i/(N*N)
label = pyglet.text.Label('t='+str(t)+' I='+str(r_i),
font_name='Helvetica', color=(255,255,255,255),
font_size=12, x=10, y=10)
label.draw()
init_state()
config = pyglet.gl.Config(double_buffer=True)
win = pyglet.window.Window(N*SCALE,N*SCALE,config=config,resizable=False)
win.set_caption('SIR Model in 2d')
@win.event
def on_draw():
glClear(GL_COLOR_BUFFER_BIT)
glClearColor(0,0,0,1)
redraw()
pyglet.clock.schedule_interval(next_frame, 1/10.0)
pyglet.app.run()
上記のコードの実行例(ただし、$R_0$が非常に大きい場合)
 練習:伝染病の封じ込め
練習:伝染病の封じ込め
感染者の初期密度や$R_0$を変えながら、感染拡大・終息の様子を確認し、長距離移動を無くすることによって、どのような効果が期待されるのかを考察しなさい。