Pythonプログラミング（ステップ４・反復処理・ローン計算）

ローンの計算の補足。

１．元金均等返済と元利均等返済

住宅購入などのために大きなお金を銀行などから借りるには、利息を支払わなければならない。 この利息も含めた借金の返済方法のうち、元金均等返済と元利均等返済について考えてみたい。

利率の解釈

まず、借金の利率は「１年あたり」で表示するのが基本である。 ここでは、年利を $R$ とする（利率は百分率ではなく、1を基準にした比率で考えることにする）。 ところが、多くのローンは毎月の返済が求められているので、1年あたりの利率を12で割った値($R/12$)を1月あたりの利率と考える。 （ただし、個人ローンなどの短期の場合は、日割りで利率を計算する場合あって、その場合は $R/365$ を1日あたりの利率とする。） 以下では、月ごとに返済するローンについて考え、各回の利子を $r$ ($= R/12$)で表すことにする。

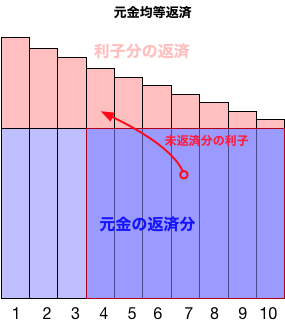
元金均等返済

あなたが $D$（円)を $n$ヶ月で返済するとしよう。 各月にこれを均等割した額（$D/n$）だけ元金を返済し、その時点での借り入れ額について利子を支払う方法を元金均等返済と呼ぶ。

最初の月（1回目）の利息額は、借金の総額が $D$ に利息がかかるので、 $$ D \times r $$ となる。 2月目の利息は、元金が減って $D - \frac{D}{n}$ になっているので $$ \left (D - \frac{D}{n} \right) \times r $$ $k$回目の利息額は $$ \left (D - D \frac{k-1}{n} \right) \times r $$ となる。このように、利息の返済分は 1回目が最も大きく、$k$ と共に、単調に（線形に）減少する。

すると、支払う利息の総額は $$ \sum_{k=1}^n \left (D - D \frac{k-1}{n} \right) \times r = D \times r \times \frac{n+1}{2} $$ となり、当然ではあるが、支払い回数 $n$ を増やせば、それだけ返済額も増えることになる。 支払い総額は、元金と合わせ、 $$ D \times \left(1 + \frac{r \times (n+1)}{2} \right) $$ となる。

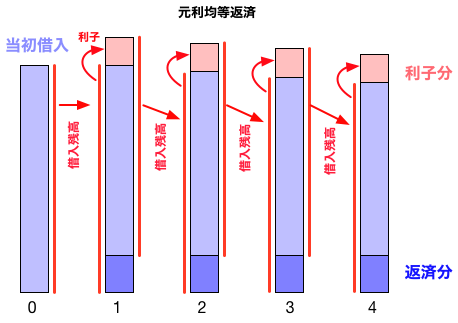
元利均等返済

毎月の返済総額（元金+利息分）を均等に返済する方式で、以下のように考える。

毎回の返済額を$x$(円)とし、完済するまで一定とする。最初の月の返済は元金に1月分の利息が膨らんだ状態から $x$ だけ返済するのであるから、 元金の総額は $$ D \times (1 + r) - x $$ となる。

2回目の返済時は、残った元金に1月分の利子が上乗せされた状態から $x$ だけ返済するのだから、元金は $$ \left\{ D \times (1 + r) - x \right\} \times (1 + r) - x $$ となる。

3回目の返済時も同様に、元金は $$ \left[ \left\{ D \times (1 + r) - x \right\} \times (1 + r) - x \right] - x $$ となる。

$k$回目の返済後の借入残高を$d_k$とおくと、漸化式 $$ d_{k} = \alpha d_{k-1} - x $$ が得られる。ただし、ここで $\alpha = 1 + r$ とおいた。

この漸化式を解くため、 $$ \begin{eqnarray} d_{k} & = & \alpha d_{k-1} - x \\ \alpha d_{k-1} & = & \alpha^2 d_{k-2} - \alpha x \\ \alpha^2 d_{k-2} & = & \alpha^3 d_{k-3} - \alpha^2 x \\ & \vdots & \\ \alpha^{k-1} d_1 & = & \alpha^k d_0 - \alpha^{k-1} x \end{eqnarray} $$ のように並べて加えると、 $$ \begin{eqnarray} d_k & = & \alpha^k d_0 - \left( 1 + \alpha + \cdots + \alpha^{k-1} \right) x \\ & = & \alpha^k d_0 - \frac{1-\alpha^k}{1-\alpha} x \end{eqnarray} $$ が得られる。ここで $d_0 = D$ である。

この結果を使うと、$k$回目の支払いで、借入残高がどれだけ減少したか（実際にどれだけ借金を返済したか）は $$ d_{k-1} - d_{k} = \left[ x - (\alpha-1) D \right] \alpha^{k-1} $$ のように（$k$の指数関数的に）変化することがわかる。 返済開始当初は、あまり借金は減らないが、ローンの終盤では、利息分に比べて実質的な返済部分が大きくなることを意味している。

$n$回で完済したいとすると、$d_n=0$となれば良いのだから、 $$ 0 = \alpha^n D - \frac{1-\alpha^n}{1-\alpha} x $$ となるような $x$ が、毎月の返済額となる。 $$ x = \frac{\alpha^n (1-\alpha)}{1-\alpha^n} D $$ 利率 $r$ の式に戻すと、 $$ x = \frac{r \; (1+r)^n }{(1+r)^n-1} D $$ となる。