情報基礎A 「アカデミックスキルII&III」（総合演習課題）

情報基礎A 「アカデミックスキルII&III」総合演習

参考情報

2020年度　レポート課題(アカデミックスキルIIおよびIII)

準備

eラーニング教材AIMD for Futureに（もしまだなら）新規登録し、教材にアクセスできるようにする。新規登録のやり方は、Classroomの「情報基礎A」の「授業」の中の「データ科学・AIの補助学習教材」の欄に書かれている。

教材、特に、最後の「実践編#1」および「実践編#2」の内容を確認する。以下は「実践編」の内容を踏まえた課題である。

課題の概要

課題1から4については全員、以下に指定したファイル名で成果物を提出すること。

課題5はボーナス課題である。提出内容に応じて、他と合わせて満点（100点）を超えない範囲での加点を行なう。ボーナス課題については、提出は任意で、真面目に取り組んでいると判断される限り、内容に間違いや不具合があっても減点は行わない。

各課題の提出ファイルは以下のとおり（課題5はボーナス課題）：

基本課題１【必須】ファイル名: 学籍番号_freq_table.py
基本課題２【必須】ファイル名: 学籍番号_mean_stdev.py
基本課題３【必須】ファイル名: 学籍番号_correlation_coef.py
基本課題４【必須】ファイル名: 学籍番号_spurious_correlation.txt
発展課題５【オプション】ファイル名: 学籍番号_covid19_cases.py

※学籍番号の箇所は、C0XB1234のように各自の学籍番号を半角文字で入れること。例：C0AB9999_freq_table.py

※提出用ファイルの作成にあたり、Windowsの場合はメモ帳(Notepad）、macOSの場合はテキストエディット(TextEdit)を用いるとよい。手順についてはこちらも確認のこと。

レポートについての連絡事項

課題内容に訂正等が生じる場合がありますので、提出前に、必ず以下を確認してください：

- 課題作成にあたり、このページに記載されている雛形プログラムはコピーして用いて構いません(2020/7/29)
- 提出ファイル名の - を _ に（ハイフンをアンダースコアに）変更しました(2020/7/29)
- 課題２の出力結果の例を修正しました(2020/8/2)
- 課題３の問題文の一部を修正しました：「新規感染者数」→「日毎の新規感染者数」（2020/8/9)

全体に渡っての要件・注意

他人（クラスメイト、ウェブ、書籍等、一切）のプログラムや提出物の一部、または全部をコピーした場合は0点（この科目は不合格）とする。
プログラムはコメントを付すなどして見やすく記述すること。「見にくい」と判断される場合は減点する。
同じ結果を与えるプログラムであっても、アルゴリズムやコーディングの上での工夫に応じて配点が異なる場合がある。また、明らかに無駄・不必要な処理、変数の未使用、等は減点の対象となる場合がある。
課題毎の要件や指示にも留意すること。
課題毎に指定されたファイル名で提出すること。 指定のファイル名で無かった場合は減点する。
提出にはGoogle Classroomを使うこと(情報基礎A / 最終課題)。メール等での提出、〆切を過ぎてからの問い合わせは一切受け付けない。提出期限は2020年8月14日(金）深夜23時59分。〆切厳守。
プログラムは、必ず動作確認をしてから提出すること。最終的にプログラムが正しく動作するところまでこぎ着けなかった場合でも、プログラム中にそのことをコメントして、作成途中のプログラムを提出すること。
Pythonプログラムについては、以下を参考に、コメント欄に氏名と学籍番号を明記すること。記入の無い場合は減点する。

課題プログラムのひな形

# 情報基礎A 課題X  学籍番号：C0XB1234 氏名：東北太郎 
# coding: utf-8

# 必要な宣言
  
# 各自のプログラムを記述

1. 基本課題

以下に示す課題１〜３のプログラムを作成し、指定されたPythonのソースプログラムを提出せよ。課題４についてはテキスト文書を提出すること。

課題１：ヒストグラム（25点）

イタリアンレストランで実施したアンケート調査によって得られた顧客の年齢構成について、各年代の人数をカウントし、出力するプログラムプログラム: 学籍番号_freq_table.py を作成せよ。

データは、下記の雛形コードの中のリストagesに設定されているので、それを用いること。

コードの雛形
（課題１、課題２共通）

# 情報基礎A 課題 X  学籍番号：C0XB1234 氏名：東北太郎                                                                                              
# coding: utf-8                                                                                                                                    

ages = [81, 75, 30, 84, 44, 56, 81, 40, 70, 52, 64, 85, 67, 65, 43, 53, 39, 52, 48,
        45, 47, 63, 56, 67, 62, 52, 59, 31, 55, 68, 61, 43, 52, 78, 56, 56, 53, 74,
        71, 59, 75, 54, 34, 35, 29, 81, 61, 46, 84, 51, 63, 63, 79, 22, 28, 38, 68,
        74, 79, 59, 13, 67, 61, 39, 38, 54, 59, 41, 61, 34, 54, 72, 58, 34, 28, 37,
        82, 43, 32, 54, 52, 57, 49, 25, 34, 74, 45, 42, 58, 50, 70, 55, 61, 46, 102,
        70, 41, 55, 72]

動作結果の例

  〜19歳: 1
20〜29歳: 5
30〜39歳: 13
40〜49歳: 15
50〜59歳: 27
60〜69歳: 16
70〜79歳: 14
80〜  　: 8
合計    : 99

課題２：平均と標準偏差（25点）

アンケートの顧客の平均年齢と年齢の標準偏差（標本標準偏差）を計算し出力するPythonプログラム: 学籍番号_mean_stdev.py を作成せよ。

データは、課題１の雛形コードの中のリストagesに設定されているので、それを用いること。

動作結果の例

データの件数：99
平均: 55.3
標準偏差: 16.5

課題３：相関係数 (25点)

イタリアンレストランで実施したアンケート調査によって得られた顧客の年齢と客単価について相関係数（ピアソンの積率相関係数）を計算し、出力するプログラムプログラム: 学籍番号_correlation_coef.py を作成せよ。

以下にコードと雛形と必要なデータ（年齢と客単価のペアのリスト）を用意したので、これを用いること。

コードの雛形（課題３）

# 情報基礎A 課題3  学籍番号：C0XB1234 氏名：東北太郎                                                                                               
# coding: utf-8                                                                                                                                    

age_vs_spending = [
    [81,5641],[75,6279],[30,3163],[84,5738],[44,4648],[56,5619],[81,4292],[40,4329],[70,6359],
    [52,4235],[64,5546],[85,4776],[67,4580],[65,5773],[43,3219],[53,4776],[39,3412],[52,4774],
    [48,3889],[45,4082],[47,4477],[63,4011],[56,5416],[67,4319],[62,6490],[52,4777],[59,4490],
    [31,2179],[55,4881],[68,4602],[61,4359],[43,4252],[52,5178],[78,5883],[56,5987],[56,5254],
    [53,5523],[74,6874],[71,5282],[59,5004],[75,6090],[54,4536],[34,2912],[35,3207],[29,2234],
    [81,6547],[61,6908],[46,4934],[84,5430],[51,5018],[63,4808],[63,5390],[79,6061],[22,983],
    [28,2197],[38,2890],[68,4747],[74,5305],[79,6507],[59,5141],[13,605],[67,4264],[61,4887],
    [39,3398],[38,2245],[54,4277],[59,5742],[41,3958],[61,5890],[34,3425],[54,5266],[72,5087],
    [58,5459],[34,2078],[28,2289],[37,2986],[82,6565],[43,4708],[32,2878],[54,4262],[52,5696],
    [57,5079],[49,3194],[25,1215],[34,3225],[74,5871],[45,4068],[42,3467],[58,5025],[50,4510],
    [70,6342],[55,4749],[61,5870],[46,4329],[102,5587],[70,5130],[41,3627],[55,4034],[72,6417]
]

動作結果の例

データの件数：99
相関係数: 0.81

ヒント

相関係数については、こちらのページを参照のこと

課題４：疑似相関(25点)

疑似相関（spurious correlation）について調べよ。

疑似相関と思われるいくつかの例が、ウェブサイトSpurious Correlationsに掲載されている。その中からひとつ以上の例を引きながら、自分自身の言葉で、250文字以内で簡潔に説明せよ。この課題では「文の引用」は認めない。参照した文献、ウェブサイトについても記載すること（ただし、参照情報は文字数に含めない）。

以下に示した「解答の書き方」に倣って解答を作成し、テキストファイル: 学籍番号_spurious_correlation.txt で提出せよ。テキストファイルの文字コードは UTF-8 とせよ。

解答の書き方

情報基礎A 課題４ 学籍番号 COXB1234  青葉太郎

疑似相関とは・・・・・・。その例として ... があり ...。


参考文献：
[1] Spurious correlations, Tyler Vigen (HACHETTE BOOKS, 2015).

２. 発展課題（オプション）

以下の課題5は全員が取り組む必要は無いが、興味や技量に応じて挑戦することを奨める。提出内容に応じて、100点を超えない範囲で加点する。

課題５：データの回帰直線の計算（最大+10点）

以下のグラフは、朝日新聞社が公開しているデータを元に、 2020年3月1日以降50日間の日毎の国内の新型コロナ(SARS-CoV-2)の累計感染者数を片対数プロットしたものである。横軸は3月1日からの経過日数で、縦軸は感染者数（累計）の常用対数値である。

図

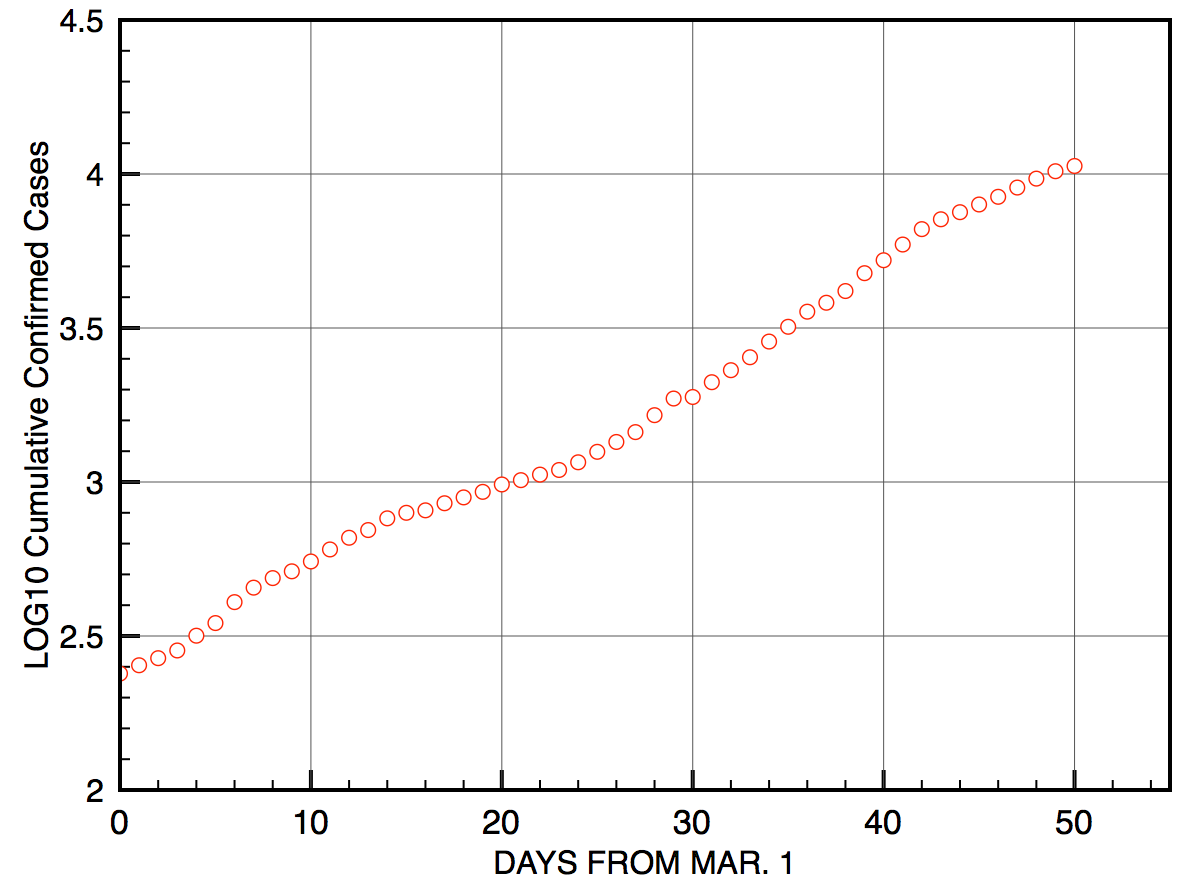
時間軸（日数）を説明変数 $x$ とし、日毎の新規感染者数の常用対数値を目的変数 $y$ とするとき、最小二乗法でデータの直線回帰 $y = a x + b$ のパラメータ $a, b$ を計算し、それらの値を出力するPythonプログラム: 学籍番号_covid19_cases.py を作成せよ。

　ヒント

最小二乗法による回帰直線の求め方については、こちらのページを参照のこと。

$t$日目の患者数を$n$とすれば、片対数プロットが直線的になるということは、患者数が指数関数的 $$ n = C \exp\left( a t \right) $$ に増加していることを表している。($C=e^b$)。

常用対数の値は、関数math.log10( )で得られる。

課題5のひな形（配列データを含む）

リストdataは、3月1日からの経過日数と累積感染者数のデータ。

# 情報基礎A 課題5 学籍番号：C0XB1234 氏名：東北太郎 
# coding: utf-8
import math

data=[
[0,239],[1,254],[2,268],[3,284],[4,317],[5,348],[6,407],
[7,454],[8,487],[9,513],[10,552],[11,604],[12,659],[13,699],
[14,762],[15,794],[16,809],[17,853],[18,892],[19,928],[20,981],
[21,1015],[22,1057],[23,1095],[24,1160],[25,1254],[26,1349],[27,1453],
[28,1647],[29,1866],[30,1887],[31,2107],[32,2306],[33,2541],[34,2855],
[35,3191],[36,3569],[37,3817],[38,4168],[39,4766],[40,5246],[41,5902],
[42,6616],[43,7123],[44,7509],[45,7964],[46,8442],[47,9027],[48,9654],
[49,10219],[50,10608]
]