Pythonプログラミング（ステップ７・最小二乗法・計算編）

このページでは、配列を用いた統計計算の例として、回帰直線をPythonで計算する方法について考える。

二つの量をペアとして表現する

実験などで二つの量の関係を調べるケースは多い（というよりは、殆どがそうなので、敢えて例を挙げるまでもないだろう）。 ここでは、$X$という量を変えながら、$Y$という量を調べている、という場合を想定しよう。

そのように、組になったデータを扱う際には、二次元リスト（リストのリスト）を用いると、すっきりとコーディングできる。 例えば、$(x,y)$ が12ペアあるようなデータを表現するには、

x_vs_y = [[1,1.9], [2,1.4], [3,5.5], [4,10.9], [5,16.5], [6,20.6],
          [7,23.7], [8,24.6], [9,20.5], [10,15.3], [11,10.0], [12,2.8]]

といった具合に記述する。

二次元リストは、数学の行列のイメージと対応する。 上の例は、$(x,y)$ で構成される行ベクトルを12個縦に並べたもの、と考えると良い： $$ \left( \begin{array}{cc} 1 & 1.9 \\ 2 & 1.4 \\ 3 & 5.5 \\ 4 & 10.9 \\ \vdots & \vdots \end{array} \right) $$

そして、リストの要素は0から始まることを思い出すと、 この例では、x_vs_y[0][0]には1、x_vs_y[0][1]には1.9が記憶されている。 x_vs_y[2][1]は、5.5 ということになる。

プログラムの中でデータをセットするには、例えば、以下のようにコーディングすれば良い：

x_vs_y=[ ]  # まずリストを用意して

....

for i in range(0,12,1):
   x_vs_y.append([i番目のxの値, i番目のyの値])  # リストにリストを追加する

　練習：二次元リスト

対応する２つの量の関係を、列ベクトルが並んだ格好、例えば、 $$ \left( \begin{array}{cc} 1 & 2 & 3 & 4 \\ 1.9 & 1.4 & 5.5 & 10.9 \\ \end{array} \right) $$ のように表現する方法も考えられる。 これに対応するPythonのリストはどのようになるか考えなさい。

量の関係を回帰直線によって特徴付ける

以下では、量 $X$ については、きちんと値が確定できるが、$Y$については、 測定の度に対象側の事情で値が揺らいだり、測定そのものに不定性（誤差）があるような組み合わせを考える。 例えば、$X$は細胞に照射された放射線量、$Y$は細胞の生存数、などを想像してみるとよい。

ここで、何らかの原因や「入力」に対応する $X$ を説明変数、 また 結果や「出力」に対応する $Y$ を目的変数と呼ぶことがある。

$X$の変化が$Y$に及ぼす影響が、揺らぎや誤差を別とすれば、直線的であることが期待されるとき、 その様子を特徴付ける方法として、最小二乗法による直線回帰が広く用いられる。 その考え方と「公式」の導出方法については、理論編のページにまとめておいたので、そちらを参照すること。

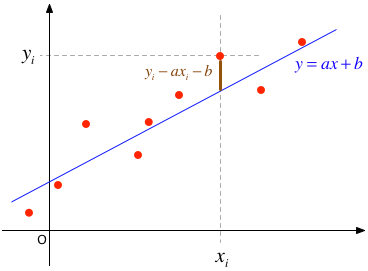
データが全部で$n$点あり、$i$番目の$X$の値を$x_i$、$Y$の値を$y_i$と表記することにする。 ここではPythonの流儀に従って、$i=0,1,2,\cdots,n-1$とする。 このデータ集合を「もっとも良く表す」ような直線（回帰直線） $y = a x + b$ の傾き $a$ と切片 $b$ は、 データから得られる統計量を使って、以下の手順で求めることができる：

【ステップ１】データ $(x_i,y_i)$ について、以下の平均量を計算する： $$ \begin{eqnarray} E(X) & = & \frac{1}{n} \sum_{i=0}^{n-1} x_i ,\\ E(XX) & = & \frac{1}{n} \sum_{i=0}^{n-1} {x_i}^2 ,\\ E(XY) & = & \frac{1}{n} \sum_{i=0}^{n-1} x_i y_i ,\\ E(Y) & = & \frac{1}{n} \sum_{i=0}^{n-1}y_i \end{eqnarray} $$

【ステップ２】こうして求めた $E(X), E(XX), E(XY), E(Y)$ を用いると、$a, b$ の値は公式 $$ \begin{eqnarray} a & = & \frac{E(XY) - E(X) E(Y)}{E(XX) - E(X)^2} ,\\ b & = & \frac{E(XX) E(Y) - E(XY) E(X)}{E(XX) - E(X)^2} \end{eqnarray} $$ から得られる。

こうして直線の傾き $a$ と切片 $b$ を決めると、データ点と直線とのy軸方向の残差の二乗和 $$ \sum_{i=0}^{n-1} \left( y_i - a x_i - b \right)^2 $$ を最小とすることができる。

　練習：地球の気温のトレンド

以下は、University of East Angliaのグループが公開しているデータを元に、 1850年から2019年までの地球上（地上と海上）の気温の変動（各地の平均気温からの変動分）をPythonのリストとして定義したものである。 これを用い、 時間（西暦年）を$X$、気温変動（temperature anomaly（度））を$Y$として、回帰直線 $y=ax+b$ のパラメータ $a,b$ を計算・表示するプログラムを作成せよ。

この期間、10年あたりに換算して、地球上の気温は平均的に何度変化したと考えられるか？

year_vs_temp = [
	[1850,-0.373],[1851,-0.218],[1852,-0.228],[1853,-0.269],[1854,-0.248],[1855,-0.272],[1856,-0.358],
	[1857,-0.461],[1858,-0.467],[1859,-0.284],[1860,-0.343],[1861,-0.407],[1862,-0.524],[1863,-0.278],
	[1864,-0.494],[1865,-0.279],[1866,-0.251],[1867,-0.321],[1868,-0.238],[1869,-0.262],[1870,-0.276],
	[1871,-0.335],[1872,-0.227],[1873,-0.304],[1874,-0.368],[1875,-0.395],[1876,-0.384],[1877,-0.075],
	[1878,0.035],[1879,-0.230],[1880,-0.227],[1881,-0.200],[1882,-0.213],[1883,-0.296],[1884,-0.409],
	[1885,-0.389],[1886,-0.367],[1887,-0.418],[1888,-0.307],[1889,-0.171],[1890,-0.416],[1891,-0.330],
	[1892,-0.455],[1893,-0.473],[1894,-0.410],[1895,-0.390],[1896,-0.186],[1897,-0.206],[1898,-0.412],
	[1899,-0.289],[1900,-0.203],[1901,-0.259],[1902,-0.402],[1903,-0.479],[1904,-0.520],[1905,-0.377],
	[1906,-0.283],[1907,-0.465],[1908,-0.511],[1909,-0.522],[1910,-0.490],[1911,-0.544],[1912,-0.437],
	[1913,-0.424],[1914,-0.244],[1915,-0.141],[1916,-0.383],[1917,-0.468],[1918,-0.333],[1919,-0.275],
	[1920,-0.247],[1921,-0.187],[1922,-0.302],[1923,-0.276],[1924,-0.294],[1925,-0.215],[1926,-0.108],
	[1927,-0.210],[1928,-0.206],[1929,-0.350],[1930,-0.137],[1931,-0.087],[1932,-0.137],[1933,-0.273],
	[1934,-0.131],[1935,-0.178],[1936,-0.147],[1937,-0.026],[1938,-0.006],[1939,-0.052],[1940,0.014],
	[1941,0.020],[1942,-0.027],[1943,-0.004],[1944,0.144],[1945,0.025],[1946,-0.071],[1947,-0.038],
	[1948,-0.039],[1949,-0.074],[1950,-0.173],[1951,-0.052],[1952,0.028],[1953,0.097],[1954,-0.129],
	[1955,-0.190],[1956,-0.267],[1957,-0.007],[1958,0.046],[1959,0.017],[1960,-0.049],[1961,0.038],
	[1962,0.014],[1963,0.048],[1964,-0.223],[1965,-0.140],[1966,-0.068],[1967,-0.074],[1968,-0.113],
	[1969,0.032],[1970,-0.027],[1971,-0.186],[1972,-0.065],[1973,0.062],[1974,-0.214],[1975,-0.149],
	[1976,-0.241],[1977,0.047],[1978,-0.062],[1979,0.057],[1980,0.092],[1981,0.140],[1982,0.011],
	[1983,0.194],[1984,-0.014],[1985,-0.030],[1986,0.045],[1987,0.192],[1988,0.198],[1989,0.118],
	[1990,0.296],[1991,0.254],[1992,0.105],[1993,0.148],[1994,0.208],[1995,0.325],[1996,0.183],
	[1997,0.390],[1998,0.539],[1999,0.306],[2000,0.294],[2001,0.441],[2002,0.496],[2003,0.505],
	[2004,0.447],[2005,0.545],[2006,0.506],[2007,0.491],[2008,0.395],[2009,0.506],[2010,0.560],
	[2011,0.425],[2012,0.470],[2013,0.514],[2014,0.579],[2015,0.763],[2016,0.797],[2017,0.677],
	[2018,0.597],[2019,0.736]
  ]

亀場で練習：グラフのプロット

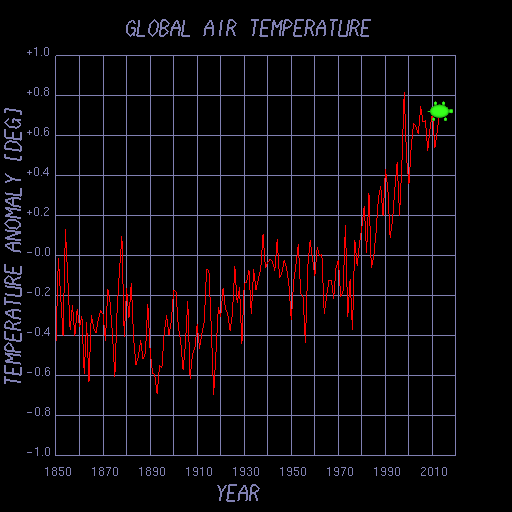
亀場を使って、西暦と気温の変動の関係のデータ（year_vs_temp)を、下図のようにプロットするプログラムを作成せよ。

加えて、最小二乗法で求めた回帰直線をグラフに重ねて描いてみよ。

　ヒント

亀場に英数字を描くにはsay( )関数やtprintf( )が使える。 また、文字のサイズを変えたり、寝かせて描く場合は、簡易プロッターライブラリを使うとよい。

　解説: matplotlibの利用

データをグラフ等で可視化する作業は、データ分析を行う上でとても重要なステップなので、その都度（上の練習問題のように） 専用のプログラムを書いていては効率が悪い。 そこで、ここでは、プロット用に用意されたライブラリ（matplotlib)を紹介しておく。

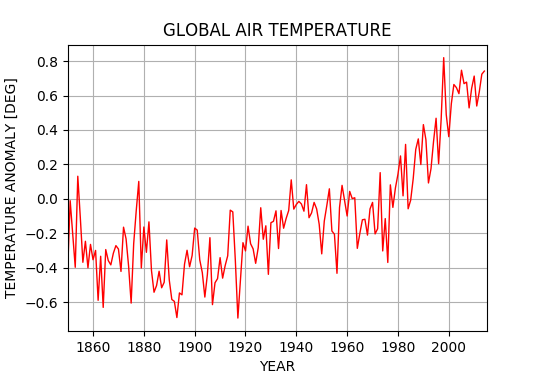
以下のコードを実行すると（注：リストを短くするため、データのリストを途中で省略してある）

# coding: utf-8
import matplotlib.pyplot as plt

year_vs_temp = [
   [1850,-0.425],[1851,-0.011],[1852,-0.208],[1853,-0.398],[1854,0.131],
   
（データは途中省略）

   [2010,0.713],[2011,0.539],[2012,0.621],[2013,0.724],[2014,0.742]
  ]

xdata = [year_vs_temp[i][0] for i in range(len(year_vs_temp)) ]
ydata = [year_vs_temp[i][1] for i in range(len(year_vs_temp)) ]

plt.title("GLOBAL AIR TEMPERATURE")
plt.plot(xdata,ydata, color=(1.0,0,0.0), linewidth=1.0)
plt.xlim(1850,2015)
plt.xlabel('YEAR')
plt.ylabel('TEMPERATURE ANOMALY [DEG]')
plt.grid(True)
plt.show()

以下のような出力が得られる。

コードの先頭付近に

import matplotlib.pyplot as plt

を記入し、以下の関数を呼び出すことで、簡単にグラフを描くことができる。 なお、ここで紹介したのはmatplotlibの機能のごく一部なので、詳しくはマニュアルやネット上の情報にあたること。

plot( )関数には上記以外にも沢山の設定項目があり、折れ線グラフ以外のタイプも選択できる。例えば、

plt.plot(xdata,ydata,'.',markersize=2.0)

は、「サイズ2.0の点マーカーでプロット」という指示になる。 詳しくはplot()関数のマニュアルを参照のこと。

非線形な関数によるフィッティング

説明変数と目的変数との関係が直線的（線形）であると期待できないような例も多くある。 むしろ、変量の関係性は本来非線形的であって、線形モデルは、それが線形に見えるような一部だけを取り出している、と考えるほうが自然かもしれない。

例えば、変量の間の関係が指数関数 $y = b e^{ax}$ で表されるような現象は広く知られている。 そのような場合、$y$の対数を取れば、 $$ z = \log(y) = a x + \log b $$ となるから、$x$と$z$の関係は線形モデルに帰着されるから、勾配$a$と切片$\log b$を最小二乗法で推定するのは容易である。

他の例としては、ロジスティック関数 $$ y = \frac{1}{1 + e^{-\beta(x-\mu)}} $$ の場合、変換 $$ z = \log\left(\frac{y}{1-y}\right) = \beta (x - \mu) $$ によって、$z$と$x$の線形な関係式に帰着できることも、よく知られている。

しかしながら、簡単な変数変換によって線形モデルに帰着できるとは限らない。

以下は、Rのサンプルデータ(cars)に基づいた、自動車の速度(km/h）と制動距離(m)の間のデータ（ファイル: cars-veloc-dist.txt)を読み込み、車速を説明変数 $x$、制動距離を目的変数 $y$ として、二次の多項式 $$ y = c_0 + c_1 x + c_2 x^2 $$ による回帰曲線を最小二乗法で求めるコードの例である。 最小二乗法によるパラメータの推定には、非線形な連立方程式を解かねばならず、線形の場合のように「公式」が無いため、 ここでは、Python用の代表的な数値計算ライブラリであるSciPyの中の optimize.leastsq( )関数 を用いた。

# coding: utf-8

from scipy import optimize
import numpy as np
import matplotlib.pyplot as plt

# 各データ点での残差を計算
def residual_err(params,x,y):
    return y - model_func(params,x)

# 回帰モデル
def model_func(params, x):
    c0 = params[0]
    c1 = params[1]
    c2 = params[2]
    return c0 + c1*x + c2*x**2

# メイン部
data = np.loadtxt('cars-veloc-dist.txt')
x = data[:,0] # veloc [km/h]
y = data[:,1] # distance [m]
init_params=[0,0,0]
params,cov = optimize.leastsq(residual_err,init_params,args=(x,y))
print('params=',params)

norder=2
v = np.linspace(5,45,100)
fitted_curve=model_func(params,v)

plt.plot(x,y, '.', color=(1.0,0,0.0), linewidth=1.0)
plt.plot(v,fitted_curve, '-', color=(0.0,0,1.0), linewidth=1.0,label="ORDER="+str(norder))
plt.xlabel('VELOC[km/h]')
plt.xlim(0,50)
plt.ylabel('BRAKING DISTANCE[m]')
plt.ylim(0,40)
plt.grid(True)
plt.legend()
plt.show()

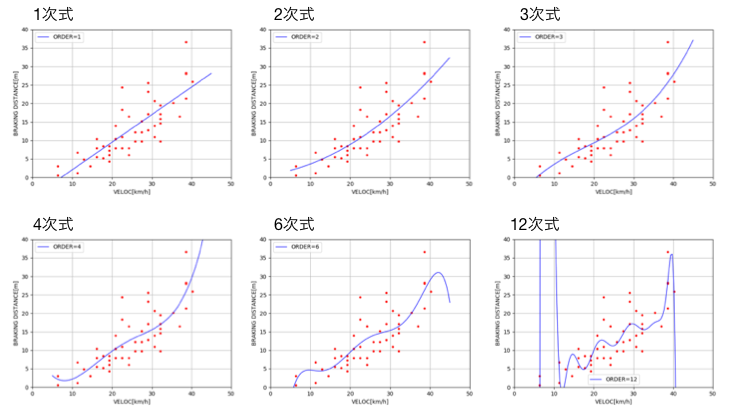
このコードを元に、多項式の次数を1,2,3,4,6,12と変え、フィッティングの様子をプロットしたのが下図である。

モデル多項式の次数を上げる（すなわちパラメータの数を増やす）ことによって、データ点との残差を小さくすることができる一方で、 データ点の無い変域では、非現実的な値を取るようになってしまう。 回帰モデルの未知のデータに対する予測性が低下している、と言っても良い。

このように、パラメータの数をいたずらに増やすことで、モデルの予測性が却って低下する現象は、オーバーフィッティング、過学習、過適合、等と呼ばれており、 データの回帰分析において、留意すべき事項のひとつである。

　練習：残差の表示

上記のコードをもとにして、回帰曲線とデータの自乗残差（residual sum of squares, RSS）を計算し、表示するように改良してみなさい。 パラメータ $\boldsymbol{c}$ の回帰モデルを $f(x ; \boldsymbol{c} )$とすれば、 $$ \textrm{RSS} = \sum_{i=0}^{N-1} \left( y_i - f(x_i ; \boldsymbol{c} ) \right)^2 $$ である。

実際に、上記の自動車の制動距離の例で、多項式の次数を増やすことで、RSSが一貫して低下する様子を確認しなさい。