Pythonプログラミング（ステップ７・統計計算・相関係数の検定）

このページでは、相関係数の検定方法について考える。（書きかけ）

ピアソンの相関係数の検定

２つの量に線形な関係性がある場合のモデル：最小二乗法

ある変量$Y$が、平均値0のガウス的なゆらぎ$\xi$を伴いながら、$X$と線形な関係にある場合、$i$番目のデータ点 $(x_i,y_i)$ は $$ y_i = a x_i + b + \xi $$ とモデル化することができて、最小二乗法を使うと、２つのパラメータは $$ a = \frac{C_{XY}}{V_{X}} $$ および $$ b = \bar{Y} - a \bar{X} $$ となる。ここで、サンプル平均を $$ \bar{X} = \frac{1}{n} \sum_i x_i, \; \bar{Y} = \frac{1}{n} \sum_i y_i $$ 二乗偏差を $$ \begin{eqnarray} V_X = \sum_i (x_i-\bar{X})^2,\; V_Y = \sum_i (y_i-\bar{Y})^2, \\ C_{XY} = \sum_i (x_i - \bar{X}) (y_i - \bar{Y}) \end{eqnarray} $$ と、それぞれ置いた。

また、確率的なゆらぎ $\xi$ が正規分布する場合、パラメータ $a$ も正規分布し、その不偏分散は $$ \begin{eqnarray} {U_a}^2 & = & \frac{1}{n-2} \frac{\sum_i (y_i - a x_i - b)^2}{V_X} \\ & = & \frac{1}{n-2} \frac{1}{V_X} \sum_i \left( y_i - \bar{Y} - \frac{C_{XY}}{V_{X}} (x_i - \bar{X}) \right)^2 \end{eqnarray} $$ となる（こちらを参照）。 ここでは、残差が正規分布することを想定しているので、${U_a}^2$（を母分散で正規化した量）はカイ二乗分布に従う。 その際、パラメータ $a$, $b$ を決める過程で $\{y_i\}$ に拘束条件が２つ課せられていることから、その自由度は$n-2$となる。

「無相関＝勾配の期待値が０」とみなして相関の有無を検定

ここで、もし$X$と$Y$の間に線形な相関関係が存在しない場合、傾き $a$ の期待値は0となるはずである。 そこで、帰無仮説として『$a$の平均が0である』を設定してみよう。そして、 $$ t = \frac{a - 0}{U_a} $$ によってt統計量を定義し、それを使って平均値の検定を行う。 ${U_a}^2$ は自由度 $n-2$ のカイ二乗分布に従うことから、$t$ は自由度 $n-2$ のt分布に従う。

ピアソンの相関係数 $r$ が $$ r = \frac{C_{XY}}{ \sqrt{V_X V_Y} } $$ であることに注意しながら、上記のt統計量を変形すると（少々煩雑な計算を経て）、 $$ t = \frac{r \sqrt{n-2}}{\sqrt{1-r^2}} $$ を得る。すなわち、相関係数 $r$ とデータの件数 $n$ を使って、帰無仮説（相関係数0）の検定を行うことができる。

スピアマンの順位相関係数の検定

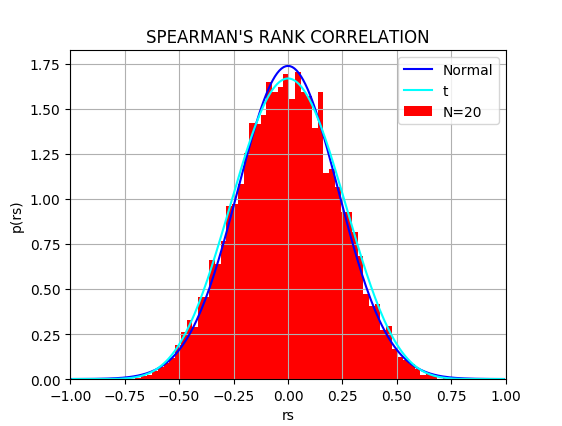
スピアマンの順位相関についても、データの件数が十分大きければ($n \gt 20$ がひとつの目安と書かれている文献が多い）、 ピアソンの相関係数の検定と同様に、t統計量 $$ t = \frac{r_s \sqrt{n-2}}{\sqrt{1-{r_s}^2}} $$ によって検定が行われている。 ただし、正確には順位差のゆらぎは正規分布しないので、件数が少ない場合は、こうした扱いをすることはできない。

「順位」に見立てた1から$N$までの自然数がランダムに並んだ２つのリストを用意し、順位差の自乗和から スピアマンの順位相関係数$r_s$を求める試行を多数回行って、$r_s$の分布を求めるコードの例を以下に示す。 リストは毎回シャッフルされるので、順位に相関は無い。 そのような状況で、観測値 robs よりも大きな値が得られた回数をカウントし、p値を推定している。

原理的にこの方法ではp値が 1/(試行回数) 以下であるようなケースを評価することはできない。

# coding: utf-8

import matplotlib.pyplot as plt
import math
import numpy as np
from scipy.stats import norm
from scipy.stats import t

N = 20
robs = 0.5

ntrial=10000

x = np.arange(1,N+1)
y = np.arange(1,N+1)
tab = []
count=0

for _ in range(ntrial):
    np.random.shuffle(x) 
    np.random.shuffle(y) 
    d2=0
    for k in range(0,N):
        d2 +=  (x[k]-y[k])**2
    rs = 1 - 6/(N**3-N)*d2
    if abs(rs) > abs(robs):
        count += 1
    tab.append(rs)

print("#sample=",N)
print("rs=",robs)
print("p-value=",count/ntrial)

xaxis = np.arange(-1, 1, 0.01)
rv1 = norm(scale=1.0/math.sqrt(N-1))
pdf1 = rv1.pdf(xaxis)

taxis = xaxis*np.sqrt(N-2)/np.sqrt(1-xaxis**2)
rv2 = t(N-2)
pdf2 = rv2.pdf(taxis) * np.sqrt(N-2)*(1 + 2*xaxis**2 * np.sqrt(1 - xaxis**2)**(-3))

plt.title("SPEARMAN'S RANK CORRELATION")
plt.hist(tab, bins=60, density=True, color=(1.0,0,0.0), label="N="+str(N))
plt.plot(xaxis,pdf1,'-',color=(0.0,0,1.0), label="Normal")
plt.plot(xaxis,pdf2,'-',color=(0.0,1.0,1.0), label="t")
plt.legend()
plt.xlim(-1,1)
plt.xlabel('rs')
plt.ylabel('p(rs)')
plt.grid(True)
plt.show()