情報基礎A 「Cプログラミング」総合演習・その準備とヒント

課題に取り組むまでの準備

亀場サーバー用のファイルはZIP形式で「圧縮」されている。

解凍後は、上のようなアイコンで表示される。

課題に取り組む前に、(1) Linux用のアプリ（亀場サーバー）と、 (2) プログラミングに必要なヘッダファイル（turtle.h)のふたつを入手しておく必要がある。

1. 亀場サーバーをダウンロードする。ダウンロード先はこちら（右クリックして「名前を付けて保存」）。
2. ダウンロードしたファイル（tfield-linux.zip）を「解凍」する。（ファイルを右クリックして、「展開」を選ぶ。展開先はデスクトップにする。）
3. turtle.hをダウンロードして、プログラミング作業用のフォルダに保存・移動する。

動作の確認

ダウンロードと解凍が完了したら、以下の手順で、動作確認を行う：

まず、亀場の解説の、タートルグラフィックスとは、と、 Linux環境について説明、亀場の様子についての記述を読んでおく。

次いで、ステップ１：C言語でプログラムを作成するを参照して、掲載されているサンプルプログラムをエディタのコピーし、ファイルに保存する(square.c)。保存先のフォルダーに、先ほどダウンロードした turtle.h があることを確認する。

亀場サーバー（tfield-linux)をダブルクリックして起動する（黒色の四角いウィンドウが現れる）

ステップ２：プログラムをコンパイルして実行するを実際に試し、亀場に赤い四角形が表示されることを確認する。

　練習：正三角形

四角形のプログラムを参考にして、画面に１辺の長さが２００の正三角形を描くプログラムを作成しなさい（位置は自由）。

描画内容のスクリーンショットを画像ファイルとして保存してみなさい。

　スクリーンショットの撮り（取り）方

この課題では、プログラム（何々.c）に加えて、亀場のスクリーンショットの提出が求められている。スクリーンショットを取る方法は以下のとおり：

1. 亀場に図形などが表示されている状態で、亀場のウィンドウのどこかをクリックして、前面に出す
2. その状態でキーボードの p キーを押す
3. ホームディレクトリ（デスクトップではない）に tfield-capture-xxxxx.png という画像ファイルが作成されているので、適宜、名前を変更する

正三角形の描画プログラム

まず、タートルグラフィックスの解説のページの「亀で描く基本的な図形」の「正Ｎ角形」の解説をよく読んでおく。

上記の解説に書かれているとおり、正三角形の場合、半径200の円に内接する正三角形の辺の長さ$s$は $$ s = 2 \times 200 \sin\left( \frac{2 \pi}{2 \times 3} \right) = 2 \times 200 \sin\left( \frac{\pi}{3} \right) $$ である。これをCプログラム風に書けば s = 2*200*sin(M_PI/3) ; となる。

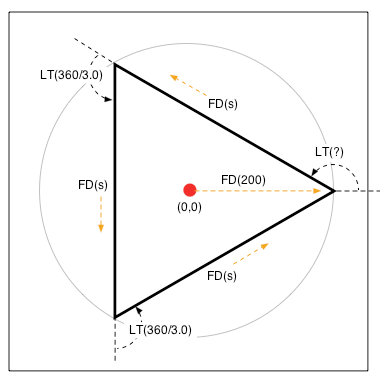
原点を中心とした半径200の円に内接する正三角形を描くには、まず、ひとつ目の頂点に移動しておく必要がある。そのためには

JUMP(0,0); /* 原点に移動する */
EAST() ;   /* 右横方向に向きを整える */
FD(200) ;  /* 200前進する */

すれば良い。

その後、「しかるべき」角度だけ左回転した後、ペンを下ろし、

FD(s) ; /* sだけ前進 */
LT(360.0/3) ; /* 120°左回転 */

を三回繰り返せば、所望の三角形が描けるはずだ（下図を参照）。

ここまでの流れをプログラムにまとめると、以下のようになる：

#include <math.h>
#include <stdio.h>
#include "turtle.h"

main()
{
    int i ;
    float s ;
    
    CON("localhost") ;
    CLR() ;
    JUMP(0,0) ;
    EAST() ;
    FD(200) ;
    LT(ある角度); /* <=== ここを考える */

    s = 2*200*sin(M_PI/3) ;
	
    PD() ;
    for (i=0; i<3 ; i=i+1) {
        FD(s) ;
        LT(360.0/3) ; 
    }
    PU() ;
}

　練習：円に内接する正三角形

上記プログラムの「ある角度」の箇所を適切に設定し、動作を確認しなさい。

うまく動いたら、さらに、線の色や太さなども調整してみなさい。

この例では「右向き」の頂点から描画を始めているが、それを「上向き」からに変更してみなさい。

正N角形のNを表す変数を用意し、その変数の値（3,4,5...)に応じてN角形が描けるように拡張しなさい。

Ｃの関数を使って、図形を部品化する

画面のあちこちに、同じような図形を描く場合に、Cの「関数」の機能がとても有用だ。関数については、ウェブ教材 C関数の基本の中で基本事項について解説を加えてあるが、 ここで必要なのは、以下で述べる使い方だけである。

辺の長さ s の正方形を描画するコード（の一部）は

EAST() ;
PD() ;
for (i=0 ; i<4 ; i=i+1) {
   FD(s) ;
   LT(90) ;
}
PU() ;

と書けるだろう。ただし、ここでは簡単のため、（外接円の中心ではなくて）正方形の左下隅の頂点を基準に、図形の配置を考えることにする。

正方形を描くプログラム（の断片）を、Cの関数として定義するには、以下のように記述する：

#include <math.h>
#include <stdio.h>
#include "turtle.h"

void square(float x, float y, float size)  /* 関数 squareの定義を開始する */
{
  int i ;     /* squreの中でだけ使う変数 i を宣言する */
  JUMP(x,y) ; /* (x,y) に移動する */
  EAST() ;    /* 右(東)を向く */
  PD() ;      /* ペンを下ろす */
  for (i=0 ; i<4 ; i=i+1) {  /* 4回繰り返す */
    FD(size) ;    /* sizeだけ前進する */
    LT(90) ;      /* 左90°回転 */
  }
  PU() ;      /* ペンを上げる */
}             /* 関数 squareの定義はここで終了 */

main()
{
  int i ;
  CON("localhost") ;
  CLR() ;

  for (i=-200 ; i<200 ; i=i+20) {
    square(i,0,10) ;  /* 座標 (i,0)にサイズ10の正方形を描く */
  }
}

上記のプログラムの

void square(float x, float y, float size)
{
   関数の記述
}

が、新たに関数 square( ) を定義している箇所になる。

このプログラム例では、main( )の中でiを-200から200まで20毎に変化させながら、square(i,0,10)を繰り返し「呼び出して」いる。すなわち、

square(-200,0,10) ;
square(-180,0,10) ;
square(-160,0,10) ;
...
square(180,0,10) ;

が順に実行され、サイズ10の正方形が、横１列にずらりと表示されるわけだ。

　練習：正方形がいっぱい

上記プログラムを手直しして、下図のように、正方形を縦横に並べて描画しなさい。

　ヒント：塗りつぶし

関数定義のところを

void square(float x, float y, float size) 
{
  int i ;     
  JUMP(x,y) ; 
  EAST() ;    
  FILL() ;  /* <== この行を追加 */
  PD() ;      
  for (i=0 ; i<4 ; i=i+1) {  
    FD(size) ;  
    LT(90) ;    
  }
  PU() ;      
}             

と変更すると、四角形の領域が塗りつぶされる（課題１（３）では、このテクニックを使用する）。