サンプルプログラム集

このページでは、いくつかサンプルプログラムを紹介します。 プログラムのコンパイルにはturtle.hが必要です。 また、実行には亀場サーバーも合わせて必要です。

C言語に不慣れな方は Cで学ぶコンピュテーショナル・シンキング もご覧ください。

フラクタル曲線

ヒルベルト曲線(Hilbert curve)を描くサンプルプログラム。描画が終わると、ロボット亀が登場するはず。
tfield-examples-hilbert-small 
#include <stdio.h>
#include <math.h>
#include "turtle.h"

#define STEP 13.0
void hilbert(int level, float angle)
{
  if (level<=0) return ;
  RT(angle) ;
  hilbert(level-1,-angle) ;
  FD(STEP) ;
  LT(angle) ;
  hilbert(level-1,angle) ;
  FD(STEP) ;
  hilbert(level-1,angle) ;
  LT(angle) ;
  FD(STEP) ;
  hilbert(level-1,-angle) ;
  RT(angle) ;
}

main()
{
  CON("localhost") ;
  CLR() ;
  RST() ;
  LW(2) ;
  COL(1.0,1.0,0.0);
  BK(200);
  LT(90);
  FD(200);
  RT(90);
  PD();
  hilbert(5,90.0);
  FIRE();
  ROBOT();
}

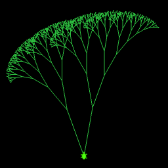
「ツリー」の描画

再帰を使って、樹形の様なパターンを描くプログラム。亀が行きつ戻りつしている様子が観察できます。
tfield-examples-tree-small 
#include "turtle.h"

void branch(float step)
{
  if (step<4.0) return ;
  else {    
    LT(20) ;
    PD() ; FD(step) ; PU() ;
    branch(step*0.6) ;
    BK(step) ;
    RT(20) ;

    RT(10) ;
    PD() ; FD(step) ; PU() ;
    branch(step*0.7) ;
    BK(step) ;
    LT(10) ;
  }
}

int main() {
  CON("localhost") ;
  CLR() ;
  RST() ;
  COL(0.1,0.7,0.2) ;
  JUMP(0,-220) ;
  NORTH() ;
  branch(150) ;
}

シェルピンスキーのガスケット

これも代表的なフラクタル図形。FILL( )モードを使っている。
tfield-examples-sierpinski-small 
#include "turtle.h"

void triangle(float size)
{
  FILL(); PD(); FD(size); LT(120); FD(size); LT(120); FD(size); PU(); LT(120);
}

void sierpinski(float size)
{
  if (size<20.0) { triangle(size) ; return ; }
  else {
    sierpinski(size/2.0) ;
    FD(size/2.0) ;
    sierpinski(size/2.0) ;
    LT(120) ;
    FD(size/2.0) ;
    RT(120) ;
    sierpinski(size/2.0) ;
    RT(120) ;
    FD(size/2.0) ;
    LT(120) ;
  }
}

main() {
  CON("localhost") ;
  CLR() ;
  JUMP(-250,-200) ;
  EAST() ;
  sierpinski(500) ;  
}

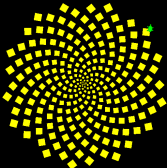
ひまわり

右回りと左まわりの螺旋が「見える」だろうか。

tfield-examples-sunflower 
#include <math.h>
#include "turtle.h"

void seed(float x, float y, float size)
{
  float step=size*sqrt(2.0) ;
  JUMP(x,y) ;
  EAST() ;
  LT(atan2(y,x)*180.0/M_PI) ;
  FD(size) ;
  LT(135) ;
  PD(); FD(step); LT(90); FD(step); LT(90); FD(step); LT(90); FD(step); PU();
}

int main()
{
  int n ;
  float x,y ;
  float GR=(1.0+sqrt(5.0))*0.5 ;
  CON("localhost") ;
  CLR();
  FILL() ;
  COL(1,1,0) ;
  for (n=1 ; n<250 ; n=n+1) {
    x = n*cos(2*M_PI/(GR*GR)*n) ;
    y = n*sin(2*M_PI/(GR*GR)*n) ;
    seed(x,y,sqrt(n)) ;
  }
}

書道

「亀」と書くプログラム。Cのプログラムとしては全く見所はありませんが、BRUSHモードを使った例として。
tfield-examples-brush-kame-small 
#include "turtle.h"

int main()
{
  int cnt ;
  CON("localhost") ;
  CLR() ;
  RST() ;
  BGC(0.8,0.8,0.7) ;
  COL(0,0,0) ;
  BRUSH() ;
  LW(30) ;
  JUMP(10,205) ;
  WEST(); LT(40) ; PD() ; FD(100) ; PU() ;
  JUMP(0,190) ; EAST() ; RT(30) ; PD() ; FD(40) ; RT(120) ; FD(100) ; PU() ;
  JUMP(-90,120) ; EAST() ; LT(5) ; 
  PD() ; FD(170) ; RT(100) ; FD(80) ; FD(0) ; PU() ;
  JUMP(-90, 100) ; SOUTH() ; LT(8) ; PD() ; FD(60) ; FD(0) ; PU() ;
  JUMP(-70, 80) ; EAST() ; LT(5) ; PD() ; FD(130) ; FD(0) ; PU() ;
  JUMP(-70, 40) ; EAST() ; LT(5) ; PD() ; FD(130) ; FD(0) ; PU() ;
  JUMP(-130,0) ; EAST() ; LT(5) ; PD() ; FD(250) ; RT(100) ; FD(90) ; FD(0) ; PU() ;
  JUMP(-120, -5) ; SOUTH() ; LT(8) ; PD() ; FD(80) ; FD(0) ; PU() ;
  JUMP(-100, -40) ; EAST() ; LT(5) ; PD() ; FD(200) ; FD(0) ; PU() ;
  JUMP(-110, -80) ; EAST() ; LT(5) ; PD() ; FD(220) ; FD(0) ; PU() ;
  LW(35) ;
  JUMP(0,110) ; SOUTH(); RT(5) ;
  PD() ; FD(210) ;
  for (cnt=0; cnt<10 ; cnt=cnt+1) {
    LT(10) ; FD(8) ; 
  }
  FD(120) ; LT(85) ; FD(50) ; PU() ;
}

雲のようなパターン

自己アフィンフラクタル（的）なパターンを生成する例。 少しリストが長くなるので、以下にリンクを設けました。 これと同様の手法が、コンピュータグラフィックスで地形や雲を生成する際に使われています。

Ｃプログラム (cloud4.c)

tfield-examples-cloud4

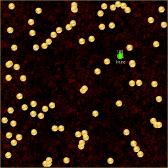
掃除ロボット

亀場にコインを100枚ばらまいてから、カメがそれを回収します。 プログラムを複数走らせることによって、複数のカメが共同でお掃除してくれます。
tfield-examples-cleaning-small 
#include "turtle.h"

void running_into_wall(unsigned int tm) {
  int cnt ;
  for (cnt=0; cnt<60; cnt++) LT(3) ;
}

void running_into_turtle(unsigned int tm) {
  int cnt ;
  for (cnt=0; cnt<40; cnt++) LT(3) ;
}

void found_coin(unsigned int tm) {
  PICKCOIN() ;
}

main() {
  int cnt,n ;
  CON("localhost") ;
  BMODE() ;
  NM("kame") ;

  SET_RUN_INTO_TURTLE_HANDLER(running_into_turtle) ;
  SET_RUN_INTO_WALL_HANDLER(running_into_wall) ;
  SET_FOUND_COIN_HANDLER(found_coin) ;

  Q_NT(&n) ;
  if (n==1) for (cnt=0; cnt<100; cnt++) COIN() ;

  for (;;) {
    FD(2) ;
    RT(0.2) ;
  }
}

コイン集め

上の例と同様に、コインを100枚散らかしてから、「コインが見つかったときに、もしコインを持っていたらその場に落とす、 持っていなければ拾う」を繰り返す例です。 ここで、「コインが見つかる」とは、「周囲にコインが無い状態からある状態に変化した」という事象のことです。 プログラムを走らせているうちに、（効率は悪いですが）だんだんとコインが集まっていく様子が観察できるはずです。

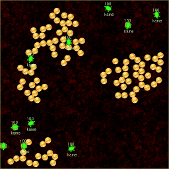
tfield-examples-coin-move-small

10匹の亀が同時にコイン集めをしている例

#include "turtle.h"

void found_coin(unsigned int tm) {
  int nc ;
  Q_MYCOIN(&nc) ;
  if (nc>0) DROPCOIN() ;
  else PICKCOIN() ;
}

void running_into_object(unsigned int tm) {
  int cnt ;
  for (cnt=0; cnt<50; cnt=cnt+1) LT(3) ;
}

main()
{
  int n,cnt ;
  CON("localhost") ;
  BMODE() ;
  NM("kame") ;

  SET_RUN_INTO_WALL_HANDLER(running_into_object) ;
  SET_RUN_INTO_TURTLE_HANDLER(running_into_object) ;
  SET_FOUND_COIN_HANDLER(found_coin) ;

  Q_NT(&n) ;
  if (n==1) for (cnt=0; cnt<100; cnt=cnt+1) COIN() ;

  while(1) {
    FD(2) ;
    RT(0.5) ;
  }
}

ハノイのカード

よく知られた「ハノイの塔」をトランプのカードを使って表示するデモ。 動作には、2017年6月版以降のバージョンの亀場サーバーとturtle.hが必要。

tfield-examples-card-hanoi

トランプによる「ハノイの塔」

#include <stdio.h>
#include "turtle.h"

int card[3][52] ;
int ncard[3]={0,0,0} ;

void redraw(int x) {
	int i, j, k ;
	CLR() ;
	for (i=0 ; i<3 ; i++) {
		for (j=0 ; j<ncard[i] ; j++) {
			k = card[i][j] ;
			CARD(k, -200 + i*150.0 - j*2, -220+j*30.0) ;
		}
	}
	JUMP(-160 + x*150.0, -140+(ncard[x]-1)*30.0) ;
}

void move_card(int x, int y) {
	if (ncard[x]>0) {
		ncard[x]-- ;
		card[y][ncard[y]] = card[x][ncard[x]] ;
		ncard[y]++ ;
	}
	redraw(y) ;
}


void move(int n, int x, int y, int z) {
	if (n==2) {
		move_card(x,z) ;
		move_card(x,y) ;
		move_card(z,y) ;
	} else {
		move(n-1,x,z,y) ;
		move_card(x,y) ;
		move(n-1,z,y,x) ;
	}
}

main()
{
	int k ;
	int n=13 ;

	CONNECT("localhost") ;
	CLR() ;
	BGC(0.1, 0.3, 0.1) ;
	NORTH() ;
	ncard[0]=n ;
	for (k=0; k<n ; k++) {
		card[0][k] = 39+n-k ;
	}
	redraw(0) ;
	move(n,0,2,1) ;
}