情報基礎A 「Cプログラミング」(ステップ3)
このステップの目標
- 分岐構造とプログラムの流れを的確に把握できる
- if文を使って、分岐のあるフローを記述できる
- C言語の条件式を正しく記述できる
1. 選択処理と分岐のあるプログラム構造
二次方程式を解くプログラム(ex3.c)
二次方程式 $a x^2 + b x + c = 0$の 係数 a,b,c を与えると、判別式を評価し、実数解を表示するプログラムの例を以下に示す:
例題3(ex3.c)
![]()
この例題は数学関数(sqrt())を用いているので,
TurtleEditを使わない(Linuxコマンドで操作する)場合には,
コンパイルするときに(前回のヘロンの公式の計算プログラムと同様に)、
cc ex3.c -lm
のようにccコマンドの最後に -lm(スペース・ハイフン・エル・エム)オプションを付けること
#include <stdio.h>
#include <math.h>
main( )
{
float a, b, c, d, s1, s2 ;
printf("係数 a b c を入力してください:") ;
scanf("%f%f%f",&a,&b,&c) ;
d = b*b - 4*a*c ;
if (d<0) {
printf("実数解はありません\n") ;
}
else {
s1 = (-b + sqrt(d))/(2*a) ;
s2 = (-b - sqrt(d))/(2*a) ;
printf("答え: %f %f\n",s1,s2) ;
}
}
プログラムを実行すると、二次方程式の係数の値を尋ねられるので、三つの数値を順にタイプしてEnterキーを押すと、実数解が(もしあれば)表示される。
 if文を使った条件分岐(選択処理)
if文を使った条件分岐(選択処理)
if文
条件によって,処理(計算)の内容を切り替えたい場合はちょくちょく登場する。 そんな場合にはif 文を使う。
if文には以下のふたつの基本形がある。
- if ( 条件式 ) 文1;
- if ( 条件式 ) 文1; else 文2;
例題3は,ちょっとややこしく見えるけれども、実は、基本形2を使った例である。
文1; や 文2; の個所は、複文(ブロック)でも構わない。ブロックとは { 何々;何々;・・・;} という風に、複数の文を{ }でひとつにまとめたものだった。ブロックはそれ全体がひとつの文のようにして扱われる(処理のひとまとまり、あるいは「段落」のようなもの)。であるから
if ( 条件式 ) { 何々; 何々 ; ・・・ } else { 何々; 何々 ; ・・・ }
という書き方も、基本形2の一種というわけだ。 それぞれの基本形を流れ図で示すと以下のようになる;
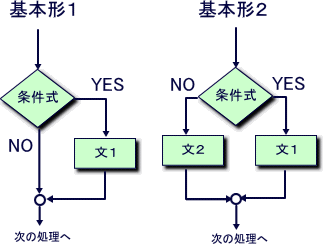
条件式
一方、条件式のところは、式の値によって、処理の流れをスイッチするための条件を、下表のようにして記述する。 表中で、a,bのところには、変数だけでなく、数式を記述することもできる(さらに詳しい記述法は、このステップの後半で学ぶ)。
| 書き方 | 内容 |
|---|---|
( a == b ) |
aとbが等しければ・・・ 等号(=) 2つであることに注意 等号ひとつ(=)は「代入」と解釈され、全く意味が異なる。 |
( a < b ) |
bが大きければ・・・ |
( a > b ) |
aが大きければ・・・ |
( a <= b ) |
bがaより大きいか,等しければ・・・ " =< " はNG |
( a >= b ) |
aがbより大きいか,等しければ・・・ " => " はNG |
( a != b ) |
aとbが等しくなければ・・・ |
例題3のその他の見所
- bの2乗は
b*bと書く(Cではb^2やb**2のような書き方は出来ない) - 平方根は sqrt(式) で表現(sqrtはSQuare RooTの略)。これを使うときは、プログラムの先頭部に
#include <math.h>を忘れずに書いておく。 (-b + sqrt(d))/(2*a)と(-b + sqrt(d))/2*aは結果が異なる。数式中の括弧の使い方に注意。
 if文の組み合わせによる複雑な分岐処理
if文の組み合わせによる複雑な分岐処理
例題3のプログラムは、係数aに0を入れると(一次方程式の場合は)、解の公式の分母が0になってしまうので、正しく計算を行うことができない。 そんな場合でも正しく処理するには、aが0の場合と、それ以外の場合で、処理方法を変えなければならない。具体的には、
もしaが0ならば、一次方程式の解を求める そうでなければ(aが0以外ならば)、以下の処理を行う: もし判別式が負値ならば、実数解なし そうでなければ、解の公式で二つの実数解を求める
といった処理の流れになるはずだ。これをCのプログラムに「翻訳」すると、
if (a==0) {
s1 = -c/b ;
printf("答え: %f\n",s1) ;
}
else {
if (d<0) {
printf("実数解はありません\n") ;
}
else {
s1 = (-b + sqrt(d))/(2*a) ;
s2 = (-b - sqrt(d))/(2*a) ;
printf("答え: %f %f\n",s1,s2) ;
}
}
となる。if文の基本形2のelseの「内部」に、さらに基本形2のif文が挿入されている点に注目。
字下げ
この例のように、複雑な条件処理をしようとすると、基本形の「何々」中に、さらにif文が「入れ子」構造(「ネスティング構造」とも言う)になる(ならざるを得ない)場合が多い。
if分を記述するときには、基本形の各パーツ毎に字下げを行うことで、どのような分岐構造になっているか、ビジュアル的にも大変わかりやすくなる
(そうしないと、それを書いた本人でさえ、プログラムの流れが判読不能に陥るだろう)。
C言語では、予約語(int, float, if, else等)、変数名、関数名(main, printf等),等以外の場所なら、どこにスペースや改行を置いても、
動作には全く影響しないルールになっている。
見かけ上もわかりやすく記述できるかどうかは、プログラム作成者の大切なセンスのひとつだ。
 練習:虚数解にも対応できるプログラム
練習:虚数解にも対応できるプログラム
さらにd<0 (虚数解)の場合に、"実部 + 虚部 i" のように計算結果が表示されるよう、プログラムを拡張してみなさい。
 ヒント
ヒント
実部と虚部をそれぞれ別個に計算しておいて、printf("%f + %f i \n", real1,imag1) ; のように表示すれば良さそうだ。
その際、必要な変数(メモリー)は適宜宣言すること。
発展:三次方程式
さらなる発展として、三次方程式の解の公式(カルダーノの公式等)を使って、
三次方程式を解く(とりあえずは、実数解のみ)プログラムに挑戦してみるのも面白いだろう。
式の途中で、三乗根の計算が必要になるが、Cでは、実数変数xの三乗根はpow(x,1.0/3.0)と表現すればよい。
もちろんxのところが数式でも構わない。
2.複雑な分岐条件の記述
上の節では、if文の全体的な構成にフォーカスを当てたが、if (条件式) {何々;}の (条件式) のパートの書き方にも、色々なバリエーションが可能だ。
| 書き方の例 | コメント |
if (a+b > c+d) ・・・ |
数式の計算結果同士の比較の例 |
if ( k%2 ) ・・・ |
ここでkはint型と仮定。k%2は、kを2で割った余り。 kが偶数の場合はk%2は0を、奇数の場合はk%2は1を与える。 C言語の条件式では、整数式の結果が0の場合は「偽」を、 それ以外(例えば1)の場合は「真」と解釈される。 つまり、この例は、「もしkが奇数ならば・・・」のC言語流の書き方 |
if ( a*a + b*b == c*c ) ・・・ |
a,b,cがint型の場合には、見てのとおりの条件式。 a,b,cがfloat型の場合(授業で説明はしていないがdouble型の場合も)、この条件式は 意図した通りに働かない可能性が高い。というのは、コンピュータは実数の 近似値を計算しているだけなので、数学的には等号が成立する場合でも、 誤差によって、計算機の内部では両辺が「完全に」等しい保証がないからだ。 例えば、 float x=2; if (sqrt(x)*sqrt(x)==x)・・・は「偽」になってしまう。 |
 複雑な条件式
複雑な条件式
論理積(かつ)、論理和(または)、否定(でない)
込み入った条件を記述しようとすると、以下のように、論理積(「かつ」)、論理和(「または」)、論理否定(「・・でない」)の組み合わせ が必要になることも多い。ここでは、以下の3つの基本的なパターンをきっちりと押さえておこう:
| 条件 | 書き方の例 | コメント |
| A かつ B |
( a > b && b > c ) |
& が二つで「かつ(and)」を表す。左の例を (a > b > c )と書いてはいけない! |
| A または B |
( a > b || a > c ) |
| が二つで「または(or)」を表す。 |
| A ではない |
( !(a > b) ) |
! は、その右側の条件式の否定。 |
 練習:三角形の面積計算
練習:三角形の面積計算
ステップ2の練習課題で、 三角形の3辺の長さa,b,cから、その面積Sを計算するプログラムを作成した。 そのときは、あまり気にしなかったけれども、a,b,cの組をあまりいいかげんに設定すると、そもそも 三角形が構成できないので、面積を計算すること自体に意味が無くなってしまうだろう(そして、ヘロンの公式の根号の中が負になってしまう)。 そこで、入力したa,b,cが三角形を構成できない場合には「三角形が構成できません」と表示するように、 面積計算のプログラムを拡張してみなさい。
 ヒント
ヒント
三角形が構成できる条件は、三角不等式 $a+b>c,\; b+c > a,\; c+a>b$ が成り立つこと。 一般に、(その意図のある無しに関わらず)間違ったデータを入力された場合を想定して、 あらかじめエラー回避を行う処理を仕込んでおく配慮が大切だ。
 発展練習:うるう年の判定
発展練習:うるう年の判定
参考:暦の計算の基本事項
ある年(西暦)がうるう年(leap year)かどうかを判断するプログラムを作成しなさい。
 ヒント
ヒント
現在採用されているグレゴリオ歴で、うるう年は以下のように定められている:
- 西暦年が4で割り切れ、かつ、100で割り切れないような年はうるう年である
- 西暦年が400で割り切れる年4で割り切れる年はうるう年である
- 上記のいずれにも該当しない年は平年である(うるう年ではない)
剰余
4で割り切れるかどうかを判断するには・・・
if ( year%4 == 0) { ・・・ }といった具合に、整数の剰余を計算する演算子%を使えばよろしい。たとえば
8%4は0を与え、 9%4は1、 10%4は2を与える。
以下に、出発点となるひな形を示しておく:
#include <stdio.h>
main()
{
int year ;
printf("year ?") ;
scanf("%d",&year) ;
if....
?????
?????
}
発展:曜日の計算
暦と日付の計算の説明を読んで、西暦年月日(y, m, d)を入力すると、 その日の曜日を出力するプログラムを作成しなさい。
 亀場で練習:三角形の描画(チェック機能付き)
亀場で練習:三角形の描画(チェック機能付き)
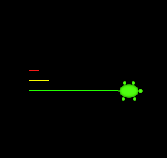
3辺の長さa,b,cを与えると、三角形が構成可能な場合は、辺がちょうどその長さになっている三角形を亀場に描き、 三角形が構成できない場合は、左図のように長さがそれぞれa,b,cの三本の線分を並べて描くプログラムを作成しなさい。
 ヒント:
ヒント:
線分の色を変えるには、PD()でペンを下ろす前にCOL()関数を呼び出す。詳しくはこちらのページを参照のこと。