情報基礎A 「Cプログラミング」（ステップ７・統計的仮説検定）

このページでは、仮説検定の例とCを使った計算方法について考える。（このページはまだ書きかけ）

データが均等にランダムか調べる：カイ二乗検定

二項分布とサンプルの偏り

紅白のボールが沢山入っている箱があって、紅と白は同数入っているはずと考えて（期待して）いる。 それを確かめたいのだけれども、ボールの数が多すぎて、全部を調べるのは断念することにした。 その代わり、無作為に中から$n$個取り出したところ、赤が$r$個、白が$w=n-r$個であった。 当初の予想は正しかったと言えるであろうか。

箱の中のボールのうち赤$p$、白が$q=1-p$の割合で入っていたと仮定すると、 $n$個の玉の中で赤が$r$個であるような確率は二項分布に従い、赤の平均は$\mu=np$、分散は$\sigma^2 = n p q$となることは良く知られている。

ここで、 $$ \chi^2 = \frac{(r-np)^2}{np} + \frac{(w-nq)^2}{nq} $$ という量を考える。$q=1-p, w=n-r$を思い出して上式を整理すると、 $$ \chi^2 = \frac{(r-np)^2}{n p q} = \left[ \frac{(r-\mu)}{\sigma} \right]^2 $$ となる。 $n$が大きければ二項分布は正規分布で良く近似できるから*、$\chi^2$（カイ二乗）、すなわち、「規格化された赤の個数の平均からの偏差の２乗」は 平均0、分散1の正規分布に従うようなランダム変数の２乗、のように振る舞うはずである。

ここで、$X_i$ の平均を$E(X_i)$ と表記することにすると、$\chi^2$は、統計学のテキストに登場する $$ \sum_i^k \frac{\left(x_i-E(X_i)\right)^2}{E(X_i)} $$ のパターン（ピアソンのカイ二乗統計量）になっている。そして、紅白ボールの場合、自由度は1（独立なランダム変数が1つで、その二乗が1回足しあわされている）である。

カイ２乗累積分布関数を計算する

それぞれが正規分布$N(0,1)$に従うような $k$ 個の独立な確率変数 $X_1, X_2, \cdots, X_k$ を２乗し、その和を取って作った確率変数 $Z = {X_1}^2 + {X_2}^2 + \cdots + {X_k}^2$ はカイ２乗分布（ガンマ分布の一種） $$ f_k(z) = \frac{z^{k/2-1} e^{-z/2}}{2^{k/2} \Gamma(k/2)} $$ に従うことが知られている。

元々のボールの数が二項分布（を近似した正規分布）すると仮定した場合に、データから得られる $Z$ が その仮定の下では、どれくらいの確率で生じるものなのかを評価するのがカイ二乗検定である。

その評価の際、カイ二乗分布の累積分布 $$ F_k(z) = \int_0^{z} f_k(y) dy $$ を計算する必要があるが、$k=2$の場合を除いて、これは数値的に求める他ない。 多くの統計学のテキスト等には数値がテーブルとして掲載されているし、表計算や統計ソフトには、標準で関数として内蔵されている。 が、残念ながら、標準的なCの数学関数には含まれていない。 なお、標準的なCの数学ライブラリにはガンマ関数$\Gamma(\ )$はtgamma( )という名前で登録されている。

紅白ボールの例では $k=1$ なので、ガンマ関数の具体的な値を入れると（$\Gamma(1/2)=\sqrt{\pi}$）、$F_1$は $$ F_1(z) = \frac{1}{\sqrt{2 \pi}} \int_0^z y^{-1/2} e^{-y/2} dy $$ となる。

$F_1(z)$を評価するため、 台形法などを使って$f_1(z)$を数値的に積分しようとしても、 積分区間の端点(0)で非積分関数が発散するので具合が悪い。そこで、部分積分して $$ \int_0^z y^{-1/2} e^{-y/2} dy = \Big[ 2 y^{1/2} e^{-y/2} \Big]_0^z + \int_0^z y^{1/2} e^{-y/2} dy $$ の形に直したこちらの式を使って計算すると良い。

検定を行なう

以上を踏まえると、検定（適合度検定）の流れは以下のようになるだろう：

「箱には赤と白のボールが同数入っている」と仮定する（帰無仮説; null hypothesis）。

次に$n,r,w$を使って$\chi^2$の値を計算する。このとき、$p=1/2$を仮定しているのだから、紅白のボールの平均は、それぞれ、$n/2$とする。

$F_1(z)$は、仮説の下で、カイ二乗の値が$z$ よりも小さくなるような確率を表している。 したがって、サンプルから得られたカイ二乗値を$\chi^2$とすると、有意水準を5%に設定した場合、 $F_1(\chi^2) \lt 0.95$であれば、そのカイ二乗値は、5%の確率でしか起こらないような「大きなずれ」の範囲の外にあることになる。 すなわち、有意水準5%で、帰無仮説は棄却されない（「統計的に有意でない」。仮説の下で、偶然そのようなサンプルが得られたと考えるほうが自然である）。

逆に、$F_1(\chi^2) \gt 0.95$ならば、仮説の下ではごく稀にしか起きないはずの範囲の中にあるので、帰無仮説は棄却される （「統計的に有意である」。仮説の下で、偶然そのようなサンプルが得られたとは考えにくい）。 その結果、「箱には赤と白のボールが同数入っていない」（対立仮説）が支持される。

統計的過誤

上のような検定は、あくまで仮定の下での可能性を議論しているので、「可能性の見積もり方が間違っている」場合と「仮定そのものが間違っている」場合の両方があり得ることに用心しなければならない：

第１種の過誤

本当に「ボールが同数」の場合であっても、 $F(\chi^2) \gt 0.95$ となってしまうような可能性が（5%の確率で）あり得ないわけではないのに、 「ボールが同数」を棄却してしまうという間違い。すなわち、5%の確率で間違った判断を犯す可能性があるわけだ。

第２種の過誤

これに対して、元々、ボールは同数でなかった場合に、たまたま$F(\chi^2) \lt 0.95$となったために、「ボールが同数」という仮説を棄却しなかった、 というタイプの間違い。

仮説検定は万能ではない

現実の複雑な現象について考える場合（例えば、ある観点から細胞のタイプを分別する場合等）、「赤」と「白」が完全に同数という状況はまずあり得ない （「完全に」正しいモデルなど存在しない、とも言える）。 「本当の」赤の確率が1/2から僅かにずれていて、$1/2+\epsilon$ $(\left| \epsilon \right| \ll 1)$ だったとすれば、 「正しい」カイ二乗値は $$ \chi^2 = \frac{\left(r-n(0.5+\epsilon)\right)^2}{n \left(0.5+\epsilon \right)\left(0.5-\epsilon \right)} \approx \frac{\left(r - 0.5 n\right)^2}{0.25 n} - 8 (r-0.5 n)\,\epsilon $$ であるべきところを、「赤」と「白」を同数と仮定した場合は、 $$ \chi^2 = \frac{\left(r - 0.5 n\right)^2}{0.25 n} $$ と見積もることになるので、両者の間には平均的に $-8 n \epsilon^2$ の差が生じる。 つまり、「赤」と「白」が同数という仮説の下で計算したカイ二乗値は、$8 n \epsilon^2$ の程度大きく見積られてしまう。 厄介なことに、この差は、サンプル数 $n$ によって加減できてしまう。 つまり、サンプル数が少なければ棄却されなかった仮説も、サンプル数を多く取ることで、いずれ棄却できてしまうことになる（$p$値を小さくすることができる）。 あるいは、そもそも、「完全に同数」という実際にあり得ない仮説を棄却すること自体に意味が無かったと言うこともできるかもしれない。 仮説検定の使用については、反省や批判もあるので、そちらも併せて調べておくのが良いだろう。 例えば、アメリカ統計学会の声明や効果量を参照。

　練習：カイ二乗検定

紅と白のボールの例について、$n,r$、および有意水準$\alpha$を入力すると、カイ二乗の適合度検定を行ない、その結果を出力するプログラムを作成せよ。

分布に「差」があるか調べる：正規性の検定

我々が扱うデータの多くは、正規性を持つ（その分布が正規分布に従う）ことが知られている。 これはある意味でノーマル(normal)な性質と言えるが、もちろん、全てがそうである（べき）というわけではない。 データセット $\{x_i\}$ が正規分布に従うかどうかを検定する方法は色々と知られているが、 ここでは、Kolmogorov-Smirnov検定（KS検定）と呼ばれる方法を使って、実際のデータを調べてみよう。

正規分布を仮定して、パラメータを推定する

$n$個のサンプル $x_i$ （$i=0,1,\cdots,n-1$）から、平均の推定値 $$ \mu = \frac{1}{n} \sum_{i=0}^{n-1} x_i $$ および、不偏分散 $$ V = \sigma^2 = \frac{n}{n-1} \left( \frac{1}{n} \sum_{i=0}^{n-1} {x_i}^2 - \mu^2 \right) $$ を計算する。 そして、実際のサンプルが、正規分布 $N(\mu,\sigma^2)$とどれくらい違っているかを調べるステップに進む。

データを小さい順に並べ変え、正規分布との差を、累積分布の上で比較する

ここでは、正規分布そのものではなく、その累積分布を考え、それとデータとの「ずれ」を考える。その、基準となる正規分布の累積分布 $$ F(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \int_{-\infty}^x \exp\left( - \frac{(t - \mu)^2}{2 \sigma^2} \right) dt $$ が計算の過程で必要となるが、Cの標準的な数学ライブラー関数には誤差関数 $$ \textrm{erf}(x) = \frac{2}{\sqrt{\pi}} \int_0^x \exp\left(- t^2 \right) dt $$ が組み込まれているので、それを使って、 $$ F(x) = \frac{1}{2} + \frac{1}{2} \textrm{erf}\left( \frac{x - \mu}{\sqrt{2} \sigma} \right) $$ と求めることができる。

では、これと比較すべきデータ点の累積分布はどう考えれば良いだろう。 データ点が$n$個あったとすると、分布の上では$x_i$の位置で$1/n$ずつの寄与となる。 （$n$点の寄与をすべて足し合わせると、1にならなければならない）。 それを累積すると、下図の赤線のように、$x_i$の位置で段差が$1/n$の折れ線になる。 この赤線と、上記の$F(x)$のずれに着目するわけである。

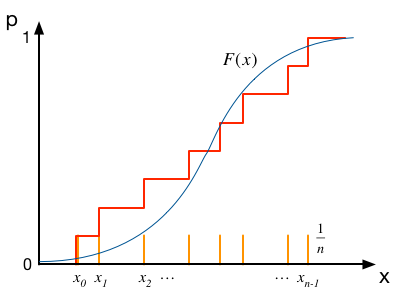
データから、その累積分布を求める手順は以下のとおりである。

まず、ソーティングのアルゴリズムを使って、$x_i$を小さい順に並べ変える。 記号が煩雑になるのを避けるため、ここでは、$x_i$はすでに小さい順に並べ変えらえた状態（$x_0 \le x_1 \le \cdots \le x_{n-1}$）にあるとして、話しを進めることにする。

すると、$i$番目の点で$p$の値は（縦軸の0から1までの区間が$n$個の点によって$n$等分されている点に注意すると）、$p_i = \frac{i+1}{n}$ となる。

分布の「ずれ」を評価する

ふたつの累積分布のずれを定量的に見積もるため、各点での縦軸方向の差を調べる。$i$番目の点$x_i$での差は、ステップの下と上で、それぞれ $$ D_i^- = \frac{i}{n} - F(x_i), \\ D_i^+ = \frac{i+1}{n} - F(x_i) $$ である。それらの中で最も大きくずれているところの絶対値を $$ D = \max_i \left\{ \max \left( |D_i^-|, |D_i^+| \right) \right\} $$ としよう。 このずれが、「もともと分布が$F(x)$であったところからのランダムな変動によって生じたものかどうか」 をテストするのがKS検定の考え方である。

ここで、関数$Q$を $$ Q(x) = 2 \sum_{j=1}^{\infty} (-1)^{j-1} \exp\left(-2j^2 x^2\right) $$ で定義すると、 「ずれ」$D$が観測されたときに、「データは元々$F(x)$に由来するものである」という帰無仮説は、（近似的に）有意水準 $$ P(D) = Q\left( \left[\sqrt{n} + 0.12 + \frac{0.11}{\sqrt{n}} \right] D \right) $$ で棄却される（詳細は専門書を参照）。 言い換えれば、検定の有意水準を$\alpha$に設定した場合、$P(D) \gt \alpha$ならば、帰無仮説（分布は$N(\mu,\sigma^2)$）は棄却されない。

　練習：KS検定

$n$個のサンプル$x_0, x_1, \cdots, x_{n-1}$を入力すると、KS検定によってデータの正規性をチェックし結果を出力するプログラムを作成せよ。

別ページの練習問題で用いたプロ野球球団の選手の体重、身長、年収のうち、正規性が見られると考えられるものはどれか。