情報基礎A 「Cプログラミング」（ステップ７・配列・ソーティング）

このページでは、配列に保存されている数の並べ替え（整列、sorting）について考える。

１．配列を使ったデータのソーティング

いきなりではあるが、身長がまちまちの人々が一列に並んでいる状態から、あなたの指示で、背の低いほうから大きい方に、順番に整列させ直したいとしよう。 このとき、（場所が大変手狭なので）、あなたが指示できることは、身長を見比べながら、列の中の二人を入れ替える操作のみ、という状況設定にしてみよう。 人数が10名くらいならば、「テキトー」にやっても、すぐに作業は完了するだろうが、100名くらいになると、きちんとした方針を立てないと、 うまくコトは運ばないだろう。

そんなとき、多くの人が自然に選択するだろう手順のひとつは、

1. まず列全体を見渡し、一番身長の低い人を見つけ、列の先頭の人と、その人の場所を入れ替える。
2. 次に、先頭から2番目より後ろの中から、（つまり、列全体で一番小柄な現在の先頭の人は除いて）一番身長の低い人を見つけ、２番目の人とその人の場所を入れ替える。
3. このように、着目する位置を後方にずらしながら、その位置よりも後方の中で一番小柄な人を見つけ、入れ替えを行う。
4. 着目する位置が列の最後尾から一人前に到達したら、作業終了

ではないだろうか。プログラミングを意識して、もう一段抽象化すると、

となる。 このアルゴリズムは、選択ソート（selection sort）と呼ばれている。 ４人の場合に、この方式で並べ替える過程を図示してみた：

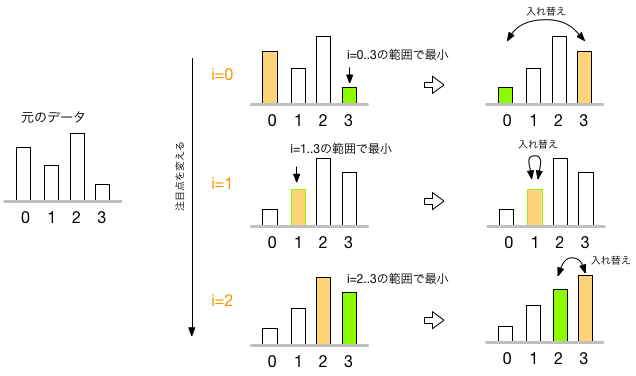
注目個所の移動

注目個所を順に後ろにずらす処理は、for文を使えば、簡単にできそうだ。敢えて書くまでも無いが(Nを人数とすると）、

   int i ;
   ・・・
   for (i = 0 ; i<N-1 ; i=i+1) { 
        配列の中の最小値の場所を見つける処理
        入れ替える処理
   }

配列の中の最小値の場所を見つける

最小値を見つけ出す処理は、前のステップの説明なども参考にすると

#include <float.h>
float data[N] ;
int i,j,k ;
float min ;
・・・
min = FLT_MAX ;
for (k=i ; k<N ; k=k+1) {
    if (data[k]<min) {
         min = data[k] ;
         j = k ;
    }
}

といった形にまとめられるはずだ。ここで、Nはデータの総数のつもり。 また、FLT_MAXは、float型で表現できる最大値を表す記号である(float型の範囲ではFLT_MAXより大きな数値は無い）。 最小値の可能性のある場所毎に、その場所（kの値）を別の変数（j）に 記録しておくところがミソである。 そうすると、ループが終了した時点で、jには、最小値が見つかった場所がセットされている。

配列の中の２つの要素を入れ替える

これは、ここまで学んだ諸君には造作無い処理のはずだ。作業用の変数（ここではw）を用意して、

float w ;
・・・
w = data[i] ;
data[i] = data[j] ;
data[j] = w ;

とすればよい。

３つの処理を組み合わせる

以上の３つの工程をひとつのプログラムに組み立ててみたのが、以下に示す例である：

#include <stdio.h>
#include <float.h>
#define N 10          /* データの総数（10）を記号Nで表す */
main( )
{
    float data[N] = { 152.1, 175.3, 177.3, 144.7, 139.2, 
                      161.2, 153.1, 185.3, 168.3, 154.8 } ;
    int i,j,k ;
    float w,min ;

    for (i=0 ; i<N-1 ; i=i+1) {   /* 注目点を１つずつ変える */
        min = FLT_MAX ;             /* 最小値の出発値をセット */
        for (k=i ; k<N ; k=k+1) {   /* iから後ろを探す */
            if (data[k]<min) {        /* より小さな値を見つけたら */
                min = data[k] ;           /* その値と、          */
                j = k ;                   /*    場所を記憶しておく */
            }
        }
        w = data[i] ;               /* iとjの内容を入れ替える */
        data[i] = data[j] ;
        data[j] = w ;
    }

    for (i=0; i<N ; i=i+1) {      /* 確認のため、データを表示 */
         printf("%f\n",data[i]) ;
    }
}

２．バブルソート

上では、「場所iより後ろで一番小さな値を探す」方針で並べ替えを行ったが、別のアプローチも可能である。 そんな中で、最も基本的とされるのが、バブルソート（bubble sort)で、 『隣り合う要素同士で大小関係を整える操作を順に行えば、最小（最大）値が配列の端に移動してくる』というアイデアに基づく。 その手順は以下のとおりである：

下図のように、隣り合う位置 $j$ と $j+1$ のデータに注目し、もしも大小関係が期待するものと逆なら、データを入れ替える、という操作を考えてみよう：

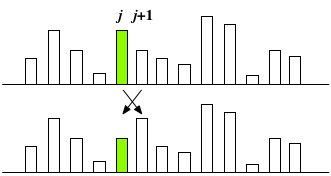
そして、この $j$ を、先頭からデータの末尾-1まで順に1つずつ動かしながら、隣同士との比較と交換を繰り返すと、 最終的に、データの末尾にはデータの中で最大の要素が来ているはずだ（下図）。 つまり、配列の最後の要素は、その順位が「確定」したことになる：

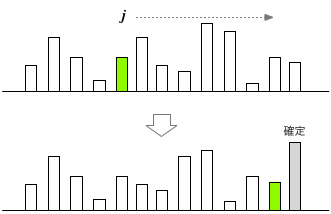
今度は、$j$を動かす範囲をひとつ狭めて同じ操作を繰り返すと、末尾から一つ前のデータが「確定」となる。 この手続きを繰り返すことによって、最終的に、全てのデータの位置を「確定」することができる（整列完了）。 具体的なアルゴリズムは：

となる。あるいは、全く同様の発想ではあるが、ループの回し方が逆のバージョン：

も可能だ（例題9a、および、教科書 例題2.25で説明されているのはこちらのバージョン）。

バブルソートでは、隣り合う要素のペアの場所を順にスライドさせ、データを一巡すると、1箇所ずつ順位が確定してゆく。 上のアルゴリズムで、$j$は着目するペアの位置、そして$i$はスライドする範囲を示す。 データが４件の場合に、第1バージョンに沿って整列が進んでいく様子を図示してみた：

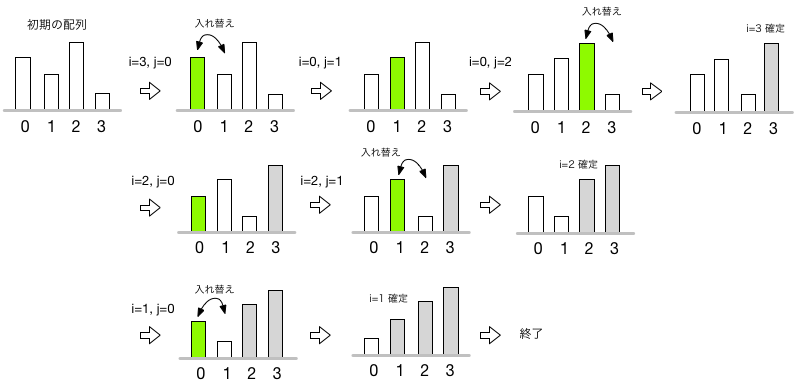
第１バージョンのアルゴリズムをCでコーディングした例を以下に示す：

#include <stdio.h>
#define N 10          /* データの総数（10）を記号Nで表す */
main( )
{
    float data[N] = { 152.1, 175.3, 177.3, 144.7, 139.2, 
                      161.2, 153.1, 185.3, 168.3, 154.8 } ;
    int i,j ;
    float w ;

    for (i=N-1; i>0 ; i=i-1) {     /* スライドする範囲の上限を１ずつ減らす */
        for (j=0 ; j<i ; j=j+1) {       /* 注目点jを0から順にi-1までスライド */
            if (data[j]>data[j+1]) {        /* 順序が違っていたら */
                w = data[j] ;                   /* jとj+1の内容を入れ替える */
                data[j] = data[j+1] ;
                data[j+1] = w ;
            }
        }
    }

    for (i=0; i<N ; i=i+1) {      /* 確認のため、データを表示 */
         printf("%f\n",data[i]) ;
    }
}

バブルソートは、選択ソートに較べ、最小値を探す手間が省ける分プログラムは簡単になるが、 その一方で、「しなくても良かった入れ替え」を何回も行なうため、作業効率は選択ソートに比べ若干悪い。

ソーティングは、データ処理のあらゆる場面に必要な基本的な作業なので、効率的なアルゴリズムが色々と研究されている。 表題に「アルゴリズム」とある教科書には必ず登場する定番のトピックなので、これから先を勉強したい者は、 図書館などで関連する書籍を探してみるとよい。

　練習：ソーティングの「速度」

このページで示した例題プログラムを修正し、乱数を使ってランダムでデータ件数の多い初期配列を生成し、それを整列させてみなさい。

　ヒント

擬似乱数の生成方法についてはこちらのページで紹介した。

データの件数(N)が100,1000,10000,...と増えるに従って、整列が完了するまでの時間がどのように変わるか「観察」してみなさい。大きなサイズの配列を宣言する場合、コンパイル時にエラー（スタックサイズ不足）となる場合がある。そのときは、配列宣言float data[N];の行を、関数宣言の外（main()の前）に移動してみるとよい。

　練習：挿入ソート

挿入ソート(insertion sort)のアルゴリズムを調べ、それに基づいて このページの例題と同じ10件のデータ（下記）を昇順に整列するコードを作成しなさい。

　ヒント

#define N 10
float data[N] = { 152.1, 175.3, 177.3, 144.7, 139.2, 161.2, 153.1, 185.3, 168.3, 154.8 } ;