情報基礎A 「Cプログラミング」（ステップ７・配列・基本的なデータ処理）

このステップの目標

配列要素の並べ替え操作を伴う処理のアルゴリズムとコードの動作を理解できる
「総和のパターン」に基づいた統計計算のプログラムが書ける

１．配列を使ったデータの整列（ソーティング）

配列を使ったデータ処理のうち、実用的にも重要な例として、配列中の数値の並び順を、小さい方から大きい方へ順に（昇順に）並べ変え、出力するプログラムを示す：

例題9a(ex9a.c)

配列データの整列（ソーティング）

#include <stdio.h>
#define N 10
main( )
{
    float x[N] = { 2.1, 5.3, 7.3, 4.7, 9.2, 1.2, 3.1, 5.3, 8.3, 4.8 } ;
    int i,j ;
    float w ;
    for (i=0 ; i<N-1 ; i=i+1) {
        for (j=N-1 ; j>i ; j=j-1) {
            if (x[j-1]>x[j]) {
                w = x[j] ;
                x[j] = x[j-1] ;
                x[j-1] = w ;
            }
        }
    }

    for (i=0; i<N ; i=i+1) {
         printf("%f\n",x[i]) ;
    }
}

例題 9aのアルゴリズム
Input: 10件のデータが入った配列 $\{x_i\}$
Output: 昇順に整列された配列 $\{x_i\}$
1: 配列$\{x_i\}$に10件のデータをセットする
2: 位置 $i$ を、先頭から末尾から1つ前まで、1ずつ「後方に」移動しながら、6:までを繰り返す:
3: 　　位置 $j$ を、末尾から $i+1$ まで、1ずつ「前に」移動しながら、5:までを繰り返す：
4: 　　　もし隣同士が $x_{j-1} \gt x_j$ ならば、$x_{j-1}$ と $x_j$ の値を入れ替える
5: 　　反復ここまで
6: 反復ここまで
7: 配列の値を先頭から順に出力する
8: 終了する

プログラムの見所

ソーティングについての補足説明はこちら

トランプのカードをバブルソートで並べ替える様子の動画（亀場を使用）

例題9の8〜16行目にかけてが、配列データの並べ変え（整列、ソーティング）を行っている部分である。 $i$ のループの中に $j$ のループが入れ子になった２重ループを形成しており、$j$ は $i$ より大きな値の範囲を動くようになっている($0 \le i \lt j \le 9$)。ここで、配列要素 x[j] で $x_j$ と表すと、例題9では、隣り合う全ての $x_{j-1}$ と $x_{j}$ のペアを参照しながら、もし $x_{j-1} \gt x_j$ ならば値を入れ替える動作を繰り返している。こうすることで、全ての$j$ について、最終的に $x_{j-1}\le x_j$ が成り立つようにできる。これは、バブルソート(bubble sort)と呼ばれるアルゴリズムに基づいたソーティングの例である。

ソーティングの仕組みについては、別ページにもう少し詳しく説明した。また、教科書例題2.25 (p.30)も併せて参照のこと。

　練習：データの整列（降順）

例題9a(ex9a.c)のコードに変更を加え、以下の80件のデータ（東北楽天ゴールデンイーグルスに登録されている選手の身長）の並びについて、値が大きいものから小さくなる順（降順）に整列されるよう改修してみなさい。

float x[80] = {
  174,175,180,185,178,184,179,185,170,178,184,183,180,191,180,180,174,188,181,182,
  187,178,175,177,185,178,175,175,174,169,174,173,185,178,180,180,183,191,179,178,
  174,185,185,180,193,181,178,181,177,176,174,180,186,180,180,180,185,174,194,175,
  183,176,192,185,186,193,171,172,175,186,180,172,175,175,177,181,178,180,176,174};

　ヒント

昇順から降順に切り替えるには、プログラム中の１箇所を変更するのみである。データの件数が変わると、プログラムのどの箇所が影響されるかについても、よく考えること。

　練習：平均とメジアン

上の課題（「データの整列」）で作成したプログラムにさらにコードを追加し、以下の例に倣って、平均値と中央値(median)を出力するよう改修してみなさい。

...
172
172
169
平均身長= ...
中央値= ...

　ヒント

平均の計算は、このページの例題9b(ex9b.c)も参照のこと。

　練習：バブルソートに要する手間

バブルソートを行なう際に、その「手間」あるいは「工数」を見積もる指標として

A. 隣同士のデータの大小を比較する回数
B. 隣同士のデータを入れ替える回数

を考えるのが良さそうである。もちろん、回数が少ないほど効率よく短時間で仕事が完了するはずである。上のデータの整列で作成したプログラムを元にして、1,2の回数をプログラム内でカウントし、

比較の回数= xxx回
入れ替えの回数 xxx回

のように出力するプログラムを作成しなさい。

２．配列を使った統計計算

以前のステップで行った統計計算プログラムを、配列を使ったバージョンに変更してみよう。先にまず、全データを配列変数に格納して、その後で、平均の計算を行っている。配列変数が登場する以外には、特に目新しい箇所は無いはずだ。

例題9b(ex9b.c)

#include <stdio.h>
#include <math.h>
main( )
{
	int n,i ;
	float x[100] ;
	float s_x, mu ;

	printf("データの件数を入れてください：") ;
	scanf("%d",&n) ;
	for (i=0 ; i<n ; i=i+1) {
		printf("%d 番目のデータ：", i+1) ;
		scanf("%f",&x[i]) ;
	}

	s_x = 0 ;
	for (i=0 ; i<n ; i=i+1) {
		s_x = s_x + x[i] ;
	}
	printf("データの総和は %f です\n",s_x) ;
	mu = s_x / n ;
	printf("平均値は %f です\n",mu) ;
}

例題9bの見所

配列の大きさは、データを入れるのに十分な数を用意しておく（例題では100）。
配列の要素は、0番目から始まる。それに対応して、ループ変数のiを0からn-1まで動かしている。
何番目のデータかを表示する際、「0番目」という表現は多少違和感があるので、i+1の値をプリントするようにしてある。

　練習：標準偏差の計算

例題9bを発展させて，平均値だけでなく標準偏差も計算して，両方を表示するプログラムを書いてみなさい。

　ヒント

標準偏差を計算は以下の手順で行えばよい：

データの件数を $n$ とし、データが $x_i$ $(x=0, \cdots, n-1)$ に格納されているとする
データの総和を求める $$S_x = \sum_{i=0}^{n-1} x_i$$
データの２乗の総和を求める $$S_{xx} = \sum_{i=0}^{n-1} (x_i)^2$$
平均 $\mu$ を求める $$\mu = \frac{S_x}{n}$$
分散 $V$ を求める $$V = \frac{S_{xx}}{n} - \mu^2$$
標準偏差 $$\sigma = \sqrt{V}$$

標準偏差の計算方法については、総和のパターンの練習も参照のこと。

総和と二乗の総和は、ひとつのforループで「まとめて」計算できるはず。

　解説: 分散（標準偏差）の推定

調査や実験から $n$ 個のサンプル $\{x_0, x_1, \cdots, x_{n-1}\}$ が得られたとしよう。そのとき、サンプルの平均は $$ \bar{x}=\frac{1}{n} \sum_{i=0}^{n-1} x_i $$ で与えられる。一方、統計学の教科書を見ると、分散（不偏分散）$\sigma^2$は、 $$ \sigma^2 = \frac{1}{n-1} \sum_{i=0}^{n-1} \left( x_i - \bar{x}\right)^2 \tag{1} $$ であると書かれている（以下では、Cの配列の流儀に合わせて、添字は0から始める）。

ところが、上の練習問題や以前の練習問題では、サンプルの分散（標本分散）を $$ s^2 = \frac{1}{n} \sum_{i=0}^{n-1} \left( x_i - \bar{x}\right)^2 \tag{2} $$ として計算している。(1)式と(2)式では、分母のところが1だけ違っているが、どちらが「正しい」のだろうか？

平均$\mu$、分散$V$に従うような多量のデータの貯蔵庫があって、観測の都度、そこから$n$個ずつデータを取り出すというイメージ。

ここの箇所、統計学の教科書には $$ E\left[\frac{X_1 + \cdots + X_n}{n}\right] = \mu \\ Var\left[\frac{X_1 + \cdots + X_n}{n}\right] = \frac{V}{n} $$ 等と表記されているかもしれない。

いま、対象としているデータの「真の」平均（母平均）が$\mu$、「真の」分散（母分散）を$V$としよう。そのとき、$n$ 個のデータ $\{x_i\}$ を独立に何回も取得（サンプリング）して得られたデータの平均値（標本平均）と真の値とのずれの２乗の期待値について $$ E\left[ \left( \frac{\sum_{i=0}^{n-1} x_i}{n} - \mu \right)^2 \right] = \frac{V}{n} \tag{3} $$ が成り立つことが知られている。ここで、$E[\cdot]$ は $\cdot$ の期待値を表す。 (3)式は、『観測によって得た平均値は真の値の周りでばらついており、そのばらつきの程度はサンプル数$n$と共に$V/n$のように変化（減少）する』と言っているわけだ。

一方、データの本来の分散は、「真の平均値$\mu$からのずれ」を使って、 $$ \frac{1}{n} \sum_{i=0}^{n-1} \left( x_i - \mu \right)^2 $$

全てのデータが等しい重みでサンプルされるとすれば、この関係はほとんど自明であろう。

で評価できる。そして、$n$の多少にかかわらず、サンプルに渡ってこれを平均すれば$V$に等しくなるはずである： $$ V = E\left[ \frac{1}{n} \sum_{i=0}^{n-1} \left( x_i - \mu \right)^2 \right] \tag{4} $$

次に、上記の量$V$と、サンプルの平均を使って求めた分散（標本分散）の期待値 $$ \tilde{V} = E\left[ \frac{1}{n} \sum_{i=0}^{n-1} \left( x_i - \frac{\sum_{i=0}^{n-1} x_i}{n} \right)^2 \right] \tag{5} $$ との差((4)式ー(5)式)を計算してみると、 $$ V - \tilde{V} = E\left[ \left( \frac{\sum_{i=0}^{n-1} x_i}{n} \right)^2 \right] - 2 \mu \,\, E\left[ \frac{\sum_{i=0}^{n-1} x_i}{n} \right] + \mu^2 $$ が得られる。ところが、上式の右辺は、式(3)（データの平均値と真の値とのずれの２乗平均）の左辺を展開した式に他ならないので、結局 $$ V - \tilde{V} = \frac{V}{n} $$ となる。知りたかったのは$V$であるから、この式を変形して、 $$ V = \frac{n}{n-1} \tilde{V} = E\left[ \frac{1}{n-1} \sum_{i=0}^{n-1} \left( x_i - \frac{\sum_{i=0}^{n-1} x_i}{n} \right)^2 \right] \tag{6} $$

つまり、「分母を$n-1$」にして計算した分散は、その期待値が$V$に等しい、ということが分かった。

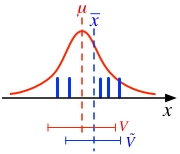
以上を定性的に再解釈すると

サンプルデータは、真の平均と比較して、より大きな値、あるいはより小さな値に偏っている可能性がある。その程度は、サンプル数 $n$ が少ないほど顕著である。
そうしたばらつきは本来分散に反映されなければならないが、例えば、値が「全体的に大きめ」であるようなサンプルに対しては、そのサンプル平均 $\bar{x}$ も当然（真の平均より）大きめとなるので、$\bar{x}$ からの平均自乗距離（すなわち標本分散）は、真の平均 $\mu$ からの平均自乗距離よりも小さく見積もられてしまう。
そうした偏り（bias）の効果まで勘定に入れて「補正」すると、分母のところが $n$ ではなく $n-1$ となる。

というわけである。